1.1.2 余弦定理 课件(35张PPT)
文档属性
| 名称 | 1.1.2 余弦定理 课件(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 00:00:00 | ||
图片预览









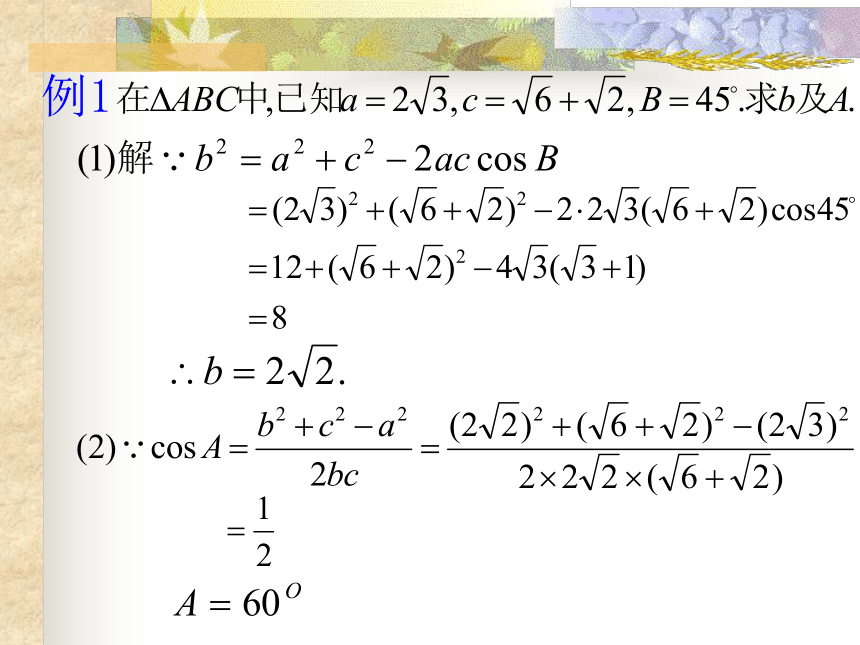
文档简介
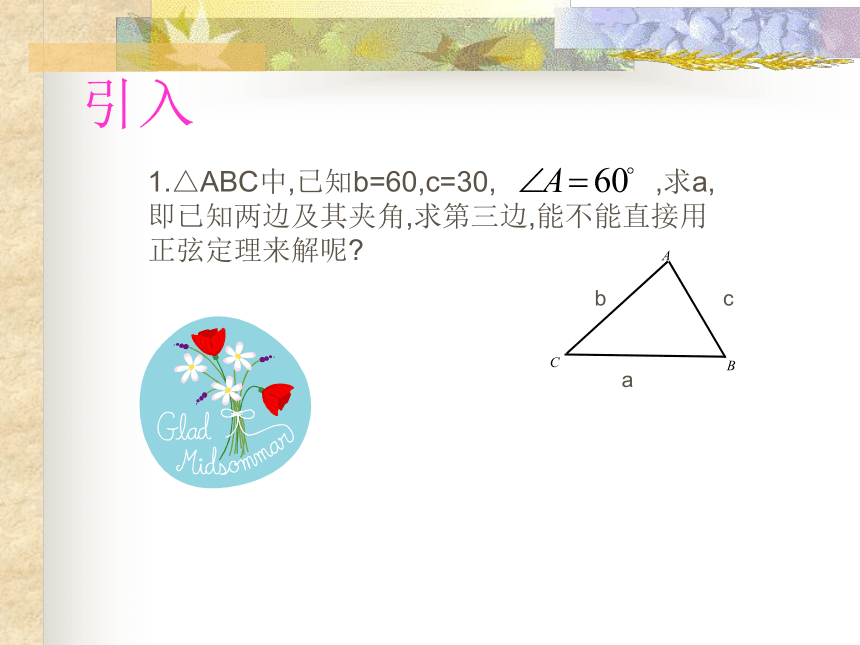
课件35张PPT。复习回顾1.正弦定理:2.可以解决两类有关三角形的问题?(1)已知两角和任一边。(2)已知两边和一边的对角。1.△ABC中,已知b=60,c=30, ,求a,即已知两边及其夹角,求第三边,能不能直接用正弦定理来解呢? 引入余 弦 定 理公式推导 如图,在△ABC中,AB、BC、CA的长分别为c、a、b.同理可证:证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:解析法证明当角C为锐角时几何法
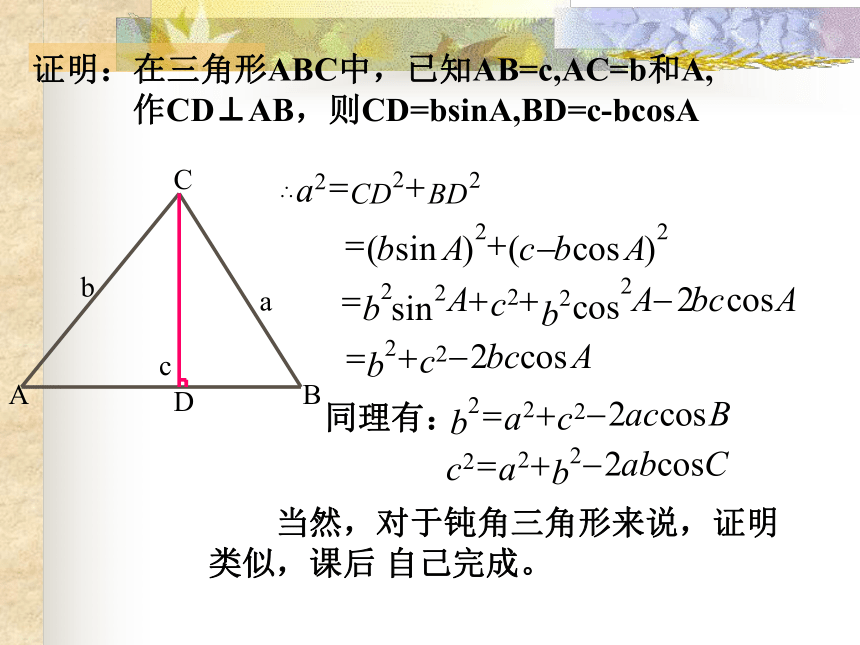
当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。证明证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA 当然,对于钝角三角形来说,证明类似,课后 自己完成。一、余弦定理 三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的两倍.余
弦
定
理公式的变式二、公式的应用 利用余弦定理,可以解决以下两类三角形的问题:
1.已知三边,求三个角;
2.已知两边和它们的夹角,求第三边和其它两个角.例1例 2:△ABC三个顶点坐标为(6,5)、(-2,8)、(4,1),求A.解法一:∴ A≈84°.解法二:∴ A≈84°.例 2:△ABC三个顶点坐标为(6,5)、(-2,8)、(4,1),求A.练习: 71~510116~912练一练:1、已知△ABC的三边为 、2、1,求它 的最大内角。变一变:
2、在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状分析:三角形ABC的形状是由大边b所对的大角B决定的。例1,a ,a+1,a+2 构成钝角三角形,求a 的取值范围。
例2,锐角三角形的三边长为2,x,3,
求x的取值范围。√5<X<√13题型一题型二题型三题型四题型五D1~510116~912综合问题题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五1~510116~912
当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。证明证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA 当然,对于钝角三角形来说,证明类似,课后 自己完成。一、余弦定理 三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的两倍.余
弦
定
理公式的变式二、公式的应用 利用余弦定理,可以解决以下两类三角形的问题:
1.已知三边,求三个角;
2.已知两边和它们的夹角,求第三边和其它两个角.例1例 2:△ABC三个顶点坐标为(6,5)、(-2,8)、(4,1),求A.解法一:∴ A≈84°.解法二:∴ A≈84°.例 2:△ABC三个顶点坐标为(6,5)、(-2,8)、(4,1),求A.练习: 71~510116~912练一练:1、已知△ABC的三边为 、2、1,求它 的最大内角。变一变:
2、在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状分析:三角形ABC的形状是由大边b所对的大角B决定的。例1,a ,a+1,a+2 构成钝角三角形,求a 的取值范围。
例2,锐角三角形的三边长为2,x,3,
求x的取值范围。√5<X<√13题型一题型二题型三题型四题型五D1~510116~912综合问题题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五1~510116~912
