1.1.2 余弦定理 课件(22张PPT)
文档属性
| 名称 | 1.1.2 余弦定理 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 634.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 22:16:54 | ||
图片预览







文档简介
课件22张PPT。§1.1.2 余弦定理一、复习回顾1、回顾正弦定理以及正弦定理能解决的解三角形
问题的类型。 (1)已知两个角和一条边
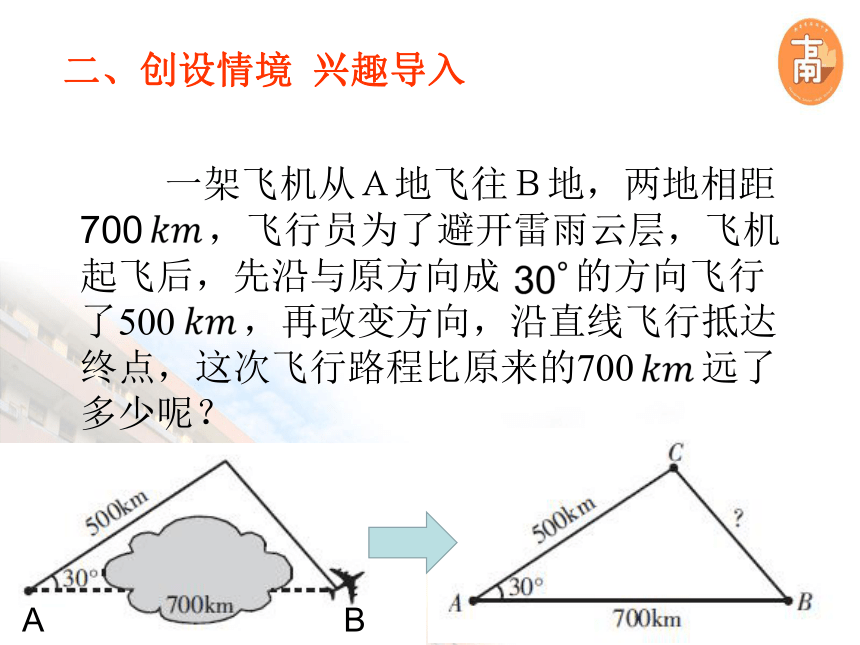
(2)已知两条边和一边的对角 正弦定理:正弦定理能解决的问题类型:二、创设情境 兴趣导入D 将长度分别为b,c的两根木棒垂直摆放,木棒另外两个端点的连线记为a,可得三边的等量关系.
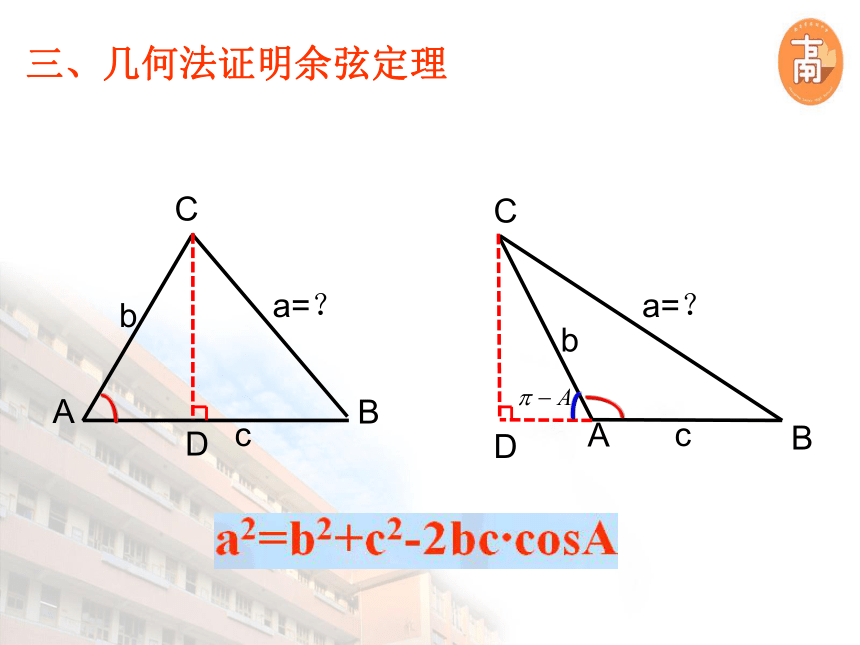
[探究][问题]当两棒的夹角变大或变小时,等式会如何变化?[问题]那么对于任意一个三角形来说,已知b,c 及A,能否得到a与b,c,A的等量关系?ABCDABCDa=?a=?bbcc三、几何法证明余弦定理ABCa=?cb综上:任意三角形,均有求谁扣谁同理可证:余弦定理 余弦定理可以看作是勾股定理的推广,勾股定理是余弦定理的特例。余弦定理:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。 应用余弦定理,我们就可以从已知的两边和夹角计算出三角形的第三条边。 利用余弦定理可以解决什么类型的三角形问题?思考:如何用文字语言来表述余弦定理?从余弦定理,可以得到它的推论四、余弦定理的推论扣谁减谁四、余弦定理的推论 应用余弦定理的推论,我们就可以从三角形的三边计算出三角形的三个角。 利用余弦定理的推论又可以解决什么类型的三角形问题?[问题] 如下刚得出的结论,反之成立吗?[问题] 已知三角形的三边,除了可以求解三角形的三个角之外,还可得到什么结论?为什么?思考A为锐角应用余弦定理,可以判定三角形的形状。cosA>0五、例题讲解 巩固提升例1:如图,在铁路建设中需要确定隧道的长度,已测得隧道两端的两点A,B到某一点C的距离分别为500米,300米,且用经纬仪(测角仪)测得其夹角为120°,求隧道的长度? 练习1.如图所示为起重机装置示意图,支杆 ,
吊杆 ,吊索 ,起吊的货物与岸
的距离 为( )
B87575875757D解:由余弦定理知A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能A解:C为最大角,由余弦定理知:因此,C为锐角87575875757 A. B.
C. D. C1.余弦定理六、知识小结4.余弦定理可以解决有关三角形的问题:3.余弦定理与三角形形状的关系5.证明余弦定理的方法
几何法
坐标法
利用正弦定理推导七、课后作业谢谢!
问题的类型。 (1)已知两个角和一条边
(2)已知两条边和一边的对角 正弦定理:正弦定理能解决的问题类型:二、创设情境 兴趣导入D 将长度分别为b,c的两根木棒垂直摆放,木棒另外两个端点的连线记为a,可得三边的等量关系.
[探究][问题]当两棒的夹角变大或变小时,等式会如何变化?[问题]那么对于任意一个三角形来说,已知b,c 及A,能否得到a与b,c,A的等量关系?ABCDABCDa=?a=?bbcc三、几何法证明余弦定理ABCa=?cb综上:任意三角形,均有求谁扣谁同理可证:余弦定理 余弦定理可以看作是勾股定理的推广,勾股定理是余弦定理的特例。余弦定理:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。 应用余弦定理,我们就可以从已知的两边和夹角计算出三角形的第三条边。 利用余弦定理可以解决什么类型的三角形问题?思考:如何用文字语言来表述余弦定理?从余弦定理,可以得到它的推论四、余弦定理的推论扣谁减谁四、余弦定理的推论 应用余弦定理的推论,我们就可以从三角形的三边计算出三角形的三个角。 利用余弦定理的推论又可以解决什么类型的三角形问题?[问题] 如下刚得出的结论,反之成立吗?[问题] 已知三角形的三边,除了可以求解三角形的三个角之外,还可得到什么结论?为什么?思考A为锐角应用余弦定理,可以判定三角形的形状。cosA>0五、例题讲解 巩固提升例1:如图,在铁路建设中需要确定隧道的长度,已测得隧道两端的两点A,B到某一点C的距离分别为500米,300米,且用经纬仪(测角仪)测得其夹角为120°,求隧道的长度? 练习1.如图所示为起重机装置示意图,支杆 ,
吊杆 ,吊索 ,起吊的货物与岸
的距离 为( )
B87575875757D解:由余弦定理知A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能A解:C为最大角,由余弦定理知:因此,C为锐角87575875757 A. B.
C. D. C1.余弦定理六、知识小结4.余弦定理可以解决有关三角形的问题:3.余弦定理与三角形形状的关系5.证明余弦定理的方法
几何法
坐标法
利用正弦定理推导七、课后作业谢谢!
