3.3 一元二次不等式及其解法 课件(18张PPT)
文档属性
| 名称 | 3.3 一元二次不等式及其解法 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 825.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 00:00:00 | ||
图片预览




文档简介
课件18张PPT。一元二次不等式解法及其应用教学目标掌握一元二次不等式的解法
掌握含参数的一元二次不等式解法
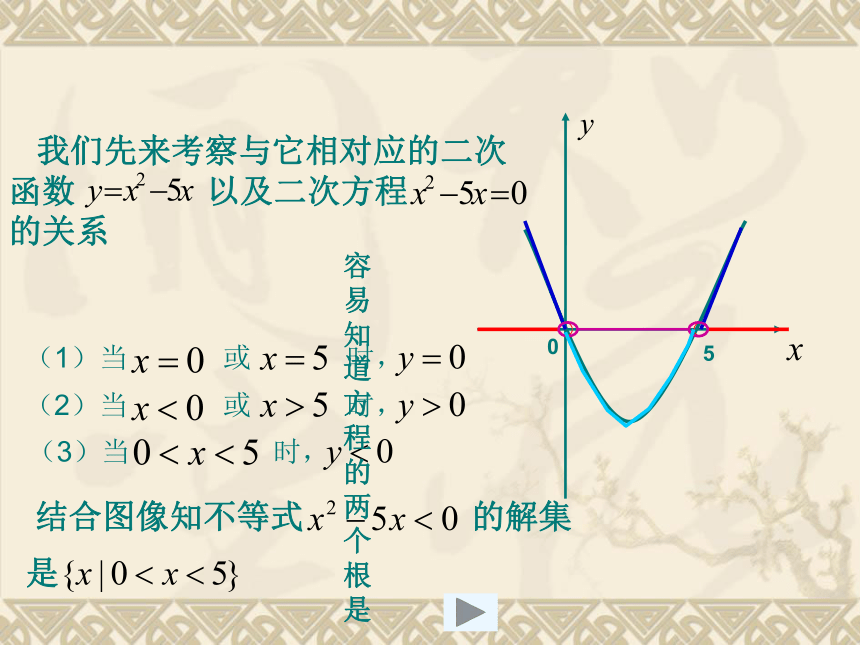
会解决一些简单的一元二次不等式恒成立问题一元二次不等式(定义)新知讲解推广:
求一般的一元二次不等式
或 的解集.并且规定
或
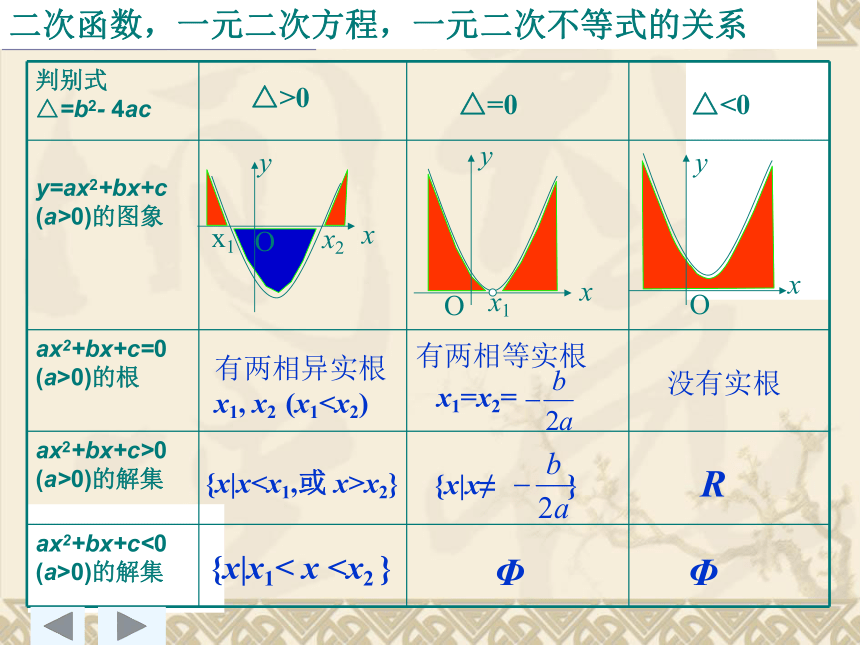
为一元二次不等式的标准形.△>0有两相异实根
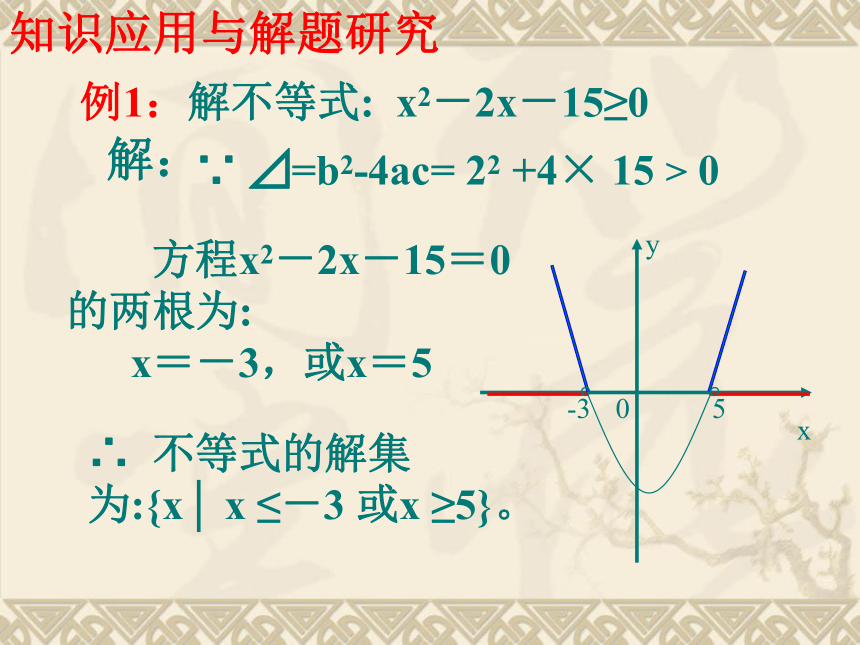
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根一元二次不等式的解法二次函数,一元二次方程,一元二次不等式的关系例1:解不等式: x2-2x-15≥0 ∵ ⊿=b2-4ac= 22 +4× 15 > 0 方程x2-2x-15=0的两根为:
x=-3,或x=5∴ 不等式的解集
为:{x│ x ≤-3 或x ≥5}。知识应用与解题研究解:总结出: 解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) (标准形)的步骤是: (1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2)判定△的符号,
(3) 求出方程ax2+bx+c=0 的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.简记为:一看—二判—三求—四写
题型与解法例4.已知不等式的解集为求a-b 的值.题型与解法例4.已知不等式的解集为求a-b 的值.题型与解法例4.已知不等式的解集为求a-b 的值.由韦达定理得一元二次不等式的恒成立问题则问题转化为m≤g(x)min解:m≤-2x2+9x在区间[2,3]上恒成立,(1)变量分离法(分离参数)例1. 关于x的不等式 在区间[ 2, 3]上恒成立,则实数m的取值范围是_______.不等式恒成立问题 【评注】对于一些含参数的不等式恒成立问题,如果能够将不等式中的变量和参数进行剥离,即使变量和参数分别位于不等式的左、右两边,然后通过求函数的值域的方法将问题化归为解关于参数的不等式的问题.问题等价于f(x)max≤0,解:构造函数(2)转换求函数的最值例1. 关于x的不等式 在区间[ 2, 3]上恒成立,则实数m的取值范围是_______.不等式恒成立问题则解:构造函数例1. 关于x的不等式 在区间[ 2, 3]上恒成立,则实数m的取值范围是_______.(3)数形结合思想不等式恒成立问题 1若不等式 (m-2)x2+2(m-2)x-4<0 对于m∈[-1,1]恒成立,则实数x 的取值范围是_______.练一练谢 谢
掌握含参数的一元二次不等式解法
会解决一些简单的一元二次不等式恒成立问题一元二次不等式(定义)新知讲解推广:
求一般的一元二次不等式
或 的解集.并且规定
或
为一元二次不等式的标准形.△>0有两相异实根
x1, x2 (x1
x=-3,或x=5∴ 不等式的解集
为:{x│ x ≤-3 或x ≥5}。知识应用与解题研究解:总结出: 解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) (标准形)的步骤是: (1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2)判定△的符号,
(3) 求出方程ax2+bx+c=0 的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.简记为:一看—二判—三求—四写
题型与解法例4.已知不等式的解集为求a-b 的值.题型与解法例4.已知不等式的解集为求a-b 的值.题型与解法例4.已知不等式的解集为求a-b 的值.由韦达定理得一元二次不等式的恒成立问题则问题转化为m≤g(x)min解:m≤-2x2+9x在区间[2,3]上恒成立,(1)变量分离法(分离参数)例1. 关于x的不等式 在区间[ 2, 3]上恒成立,则实数m的取值范围是_______.不等式恒成立问题 【评注】对于一些含参数的不等式恒成立问题,如果能够将不等式中的变量和参数进行剥离,即使变量和参数分别位于不等式的左、右两边,然后通过求函数的值域的方法将问题化归为解关于参数的不等式的问题.问题等价于f(x)max≤0,解:构造函数(2)转换求函数的最值例1. 关于x的不等式 在区间[ 2, 3]上恒成立,则实数m的取值范围是_______.不等式恒成立问题则解:构造函数例1. 关于x的不等式 在区间[ 2, 3]上恒成立,则实数m的取值范围是_______.(3)数形结合思想不等式恒成立问题 1若不等式 (m-2)x2+2(m-2)x-4<0 对于m∈[-1,1]恒成立,则实数x 的取值范围是_______.练一练谢 谢
