3.3 一元二次不等式及其解法 课件(32张PPT)
文档属性
| 名称 | 3.3 一元二次不等式及其解法 课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 544.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 22:36:08 | ||
图片预览








文档简介
课件32张PPT。§3.2 一元二次不等式及其解法复习:一元二次方程与二次函数因式分解法(十字相乘)公式法:韦达定理开口方向;对称轴顶点 坐标a>0 开口向上a<0 开口向下一元二次不等式 的定义互动探究 发现规律探究:一元二次不等式 的解集
问题:探究:一元二次方程、一元二次函数、与二次不等式的关系(1)一元二次方程 的根?(2)二次函数 图像的关系(3)一元二次方程 的根与二次
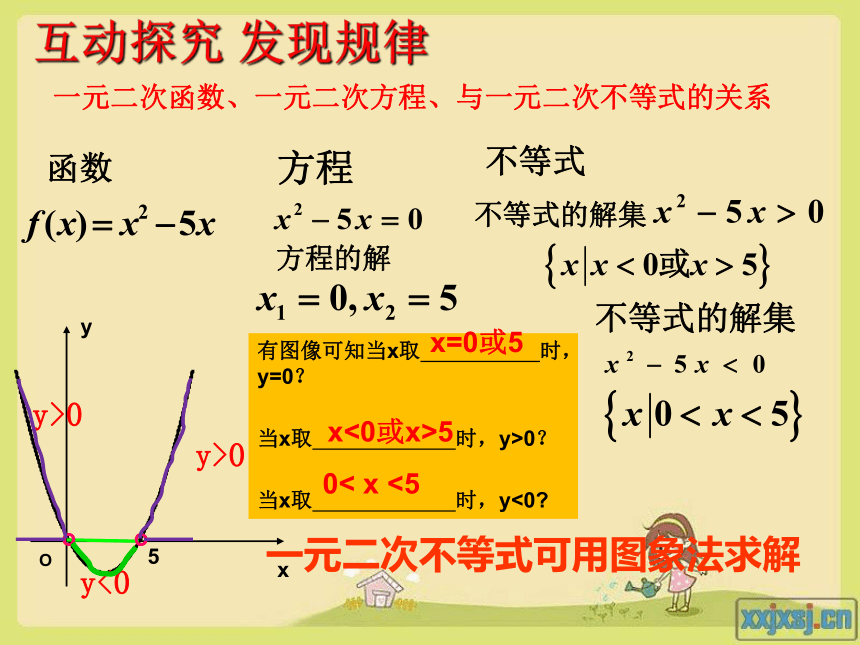
函数 图像的关系: 5函数方程不等式方程的解不等式的解集不等式的解集y>0y>0y<0一元二次函数、一元二次方程、与一元二次不等式的关系一元二次不等式可用图象法求解互动探究 发现规律有图像可知当x取 时,y=0?
当x取 时,y>0?
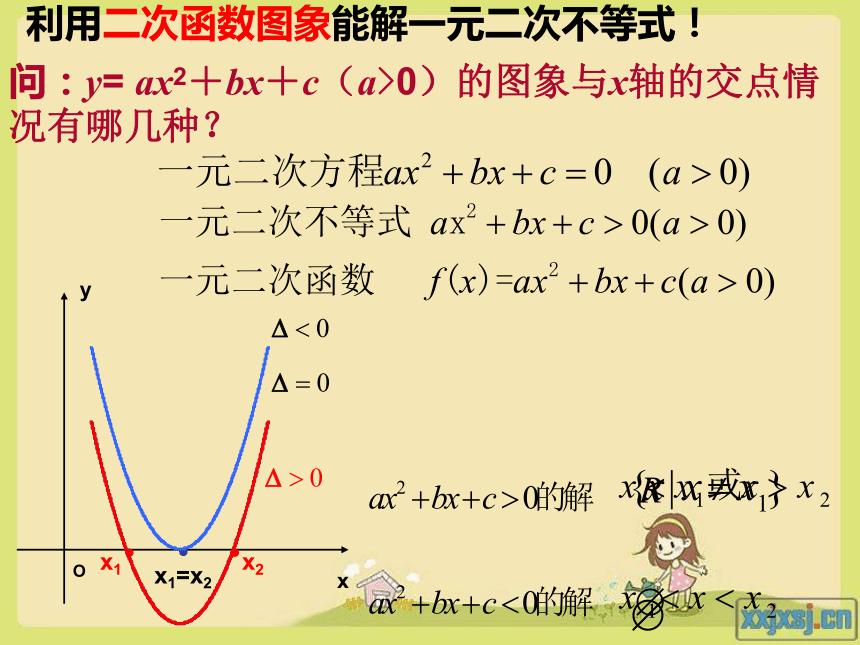
当x取 时,y<0? x=0或50< x <5x<0或x>5 oo利用二次函数图象能解一元二次不等式! 问:y= ax2+bx+c(a>0)的图象与x轴的交点情况有哪几种?△>0有两相异实根
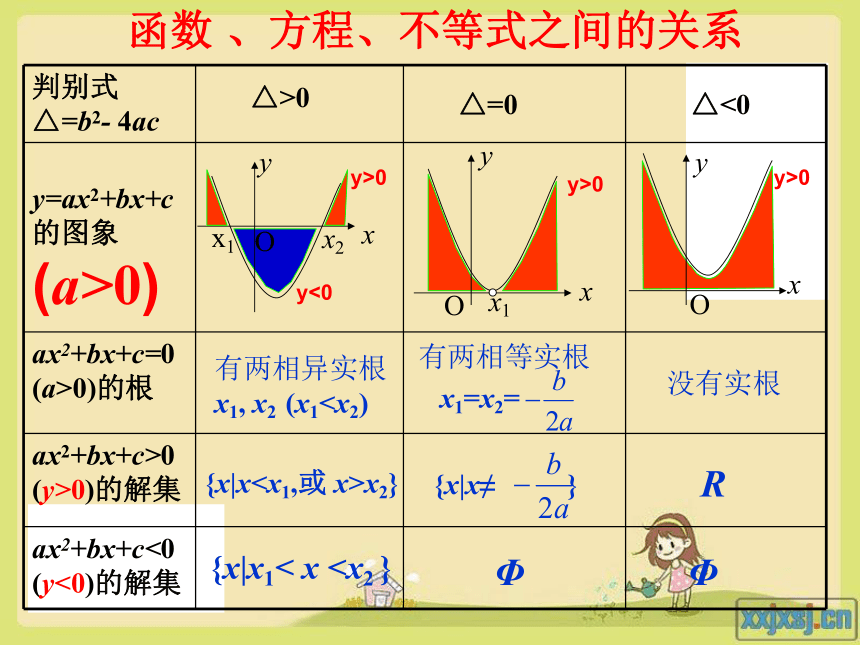
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根函数 、方程、不等式之间的关系y>0y>0y>0y<0点评例1.解不等式 2x2-3x-2 > 0 .解:因为△ =(-3)2-4×2×(-2)>0,方程的解2x2-3x-2 =0的解是所以,原不等式的解集是先求方程的根然后想像图象形状注:开口向上,大于0
解集是大于大根,小于小根(两边飞)若改为:不等式 2x2-3x-2 < 0 .注:开口向上,小于0
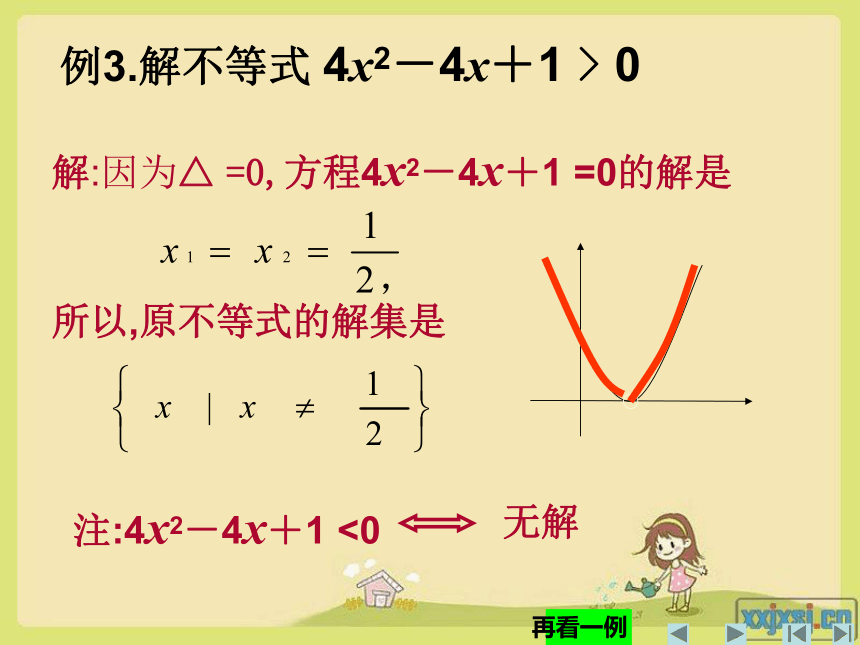
解集是大于小根且小于大根(两边夹)图象为:小结:利用二次函数图象解一元二次不等式其方法步骤是:(1)先求出Δ和相应方程的解,(2)再画出二次函数图象,根据图象写出不等式的解。若a<0时,先变形!跟踪练习:求不等式解集再看一例例3.解不等式 4x2-4x+1 > 0 注:4x2-4x+1 <0例2.解不等式 -3x2+6x > 2解: ∵-3x2+6x > 23x2-6x+2 < 0∵方程的解3x2-6x+2 =0的解是所以,原不等式的解集是若a<0时,先变形!例4.解不等式 -x2 +2x-3 > 0 注:x2 -2x+3 >0跟踪练习课本第80页第1题(3),例4.某种牌号的汽车在水泥路面上的刹车距离s m和汽车车速x km/h有如下关系: 在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01 km/h)例4.某种牌号的汽车在水泥路面上的刹车距离s m和汽车车速x km/h有如下关系: 在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01 km/h) 现有A和B两家网络服务公司,它们的资费标准为:
A公司:每小时收费1.5元(不足一小时按一小时计算)
B公司:用户上网的第一小时内(含1小时,下同)收费1.7元,第二小时内收费1.6元,以后每小时减少0.1元.(若用户一次上网时间超过17小时,按17小时计算)(一般来说,一次上网时间不会超过17小时)所以<不妨设该同学一次上网总小于17小时>
那么一次上网在多长时间以内能够保证选择电信比选择联通所需要费用少?引入分析:如果能够保证选择A公司比选择联通公司所需费用少,则有则A公司的收取费用为1.5x(元)B收费每小时依次为:1.7 ,1.6,1.5 ,1.4……(元)这是什么?其方法步骤是:(1)先求出Δ和相应方程的解,注:若a<0时,先变形!(2)再画出函数图象,根据图象写出不等式的解。2. 二次函数一元二次不等式的解一元二次方程的根图象三个二次问题都可以通过图形实现转换小结:1.利用一元二次函数图象解一元二次不等式 3.2一元二次不等式 及其解法(第二课)一、解分式不等式
问题:探究:一元二次方程、一元二次函数、与二次不等式的关系(1)一元二次方程 的根?(2)二次函数 图像的关系(3)一元二次方程 的根与二次
函数 图像的关系: 5函数方程不等式方程的解不等式的解集不等式的解集y>0y>0y<0一元二次函数、一元二次方程、与一元二次不等式的关系一元二次不等式可用图象法求解互动探究 发现规律有图像可知当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0? x=0或50< x <5x<0或x>5 oo利用二次函数图象能解一元二次不等式! 问:y= ax2+bx+c(a>0)的图象与x轴的交点情况有哪几种?△>0有两相异实根
x1, x2 (x1
解集是大于大根,小于小根(两边飞)若改为:不等式 2x2-3x-2 < 0 .注:开口向上,小于0
解集是大于小根且小于大根(两边夹)图象为:小结:利用二次函数图象解一元二次不等式其方法步骤是:(1)先求出Δ和相应方程的解,(2)再画出二次函数图象,根据图象写出不等式的解。若a<0时,先变形!跟踪练习:求不等式解集再看一例例3.解不等式 4x2-4x+1 > 0 注:4x2-4x+1 <0例2.解不等式 -3x2+6x > 2解: ∵-3x2+6x > 23x2-6x+2 < 0∵方程的解3x2-6x+2 =0的解是所以,原不等式的解集是若a<0时,先变形!例4.解不等式 -x2 +2x-3 > 0 注:x2 -2x+3 >0跟踪练习课本第80页第1题(3),例4.某种牌号的汽车在水泥路面上的刹车距离s m和汽车车速x km/h有如下关系: 在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01 km/h)例4.某种牌号的汽车在水泥路面上的刹车距离s m和汽车车速x km/h有如下关系: 在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01 km/h) 现有A和B两家网络服务公司,它们的资费标准为:
A公司:每小时收费1.5元(不足一小时按一小时计算)
B公司:用户上网的第一小时内(含1小时,下同)收费1.7元,第二小时内收费1.6元,以后每小时减少0.1元.(若用户一次上网时间超过17小时,按17小时计算)(一般来说,一次上网时间不会超过17小时)所以<不妨设该同学一次上网总小于17小时>
那么一次上网在多长时间以内能够保证选择电信比选择联通所需要费用少?引入分析:如果能够保证选择A公司比选择联通公司所需费用少,则有则A公司的收取费用为1.5x(元)B收费每小时依次为:1.7 ,1.6,1.5 ,1.4……(元)这是什么?其方法步骤是:(1)先求出Δ和相应方程的解,注:若a<0时,先变形!(2)再画出函数图象,根据图象写出不等式的解。2. 二次函数一元二次不等式的解一元二次方程的根图象三个二次问题都可以通过图形实现转换小结:1.利用一元二次函数图象解一元二次不等式 3.2一元二次不等式 及其解法(第二课)一、解分式不等式
