3.5.2 简单线性规划 课件(17张PPT)
文档属性
| 名称 | 3.5.2 简单线性规划 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 103.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 22:38:44 | ||
图片预览






文档简介
课件17张PPT。简单线性规划1.二元一次不等式表示平面区域复习思考:确定步骤:
直线定界,特殊点定域;
若C≠0,则直线定界,原点定域;2、若不等式中不含0,则边界应画成虚线,否则应画成实线。1. 情境引入导学 已知4枝玫瑰与5枝康乃馨的价格之和小于22元,而6枝玫瑰与3枝康乃馨的价格之和大于24元,则2枝玫瑰的价格与3枝康乃馨的价格哪个更高?
2.线性规划的有关概念
(1)把要求最大值或最小值的函数叫做目标函数.
(2)目标函数中的变量所满足的不等式组称为约束条件.
(3)如果目标函数是关于变量的一次函数,则称为线性目标函数.(4)如果约束条件是关于变量的一次不等式(或等式),则称为线性约束条件.
(5)在线性约束条件下,求线性目标函数的最大值或最小值问题,称为线性规划问题.(6)满足线性约束条件的解(x,y)叫做可行解.由所有可行解组成的集合叫做可行域.
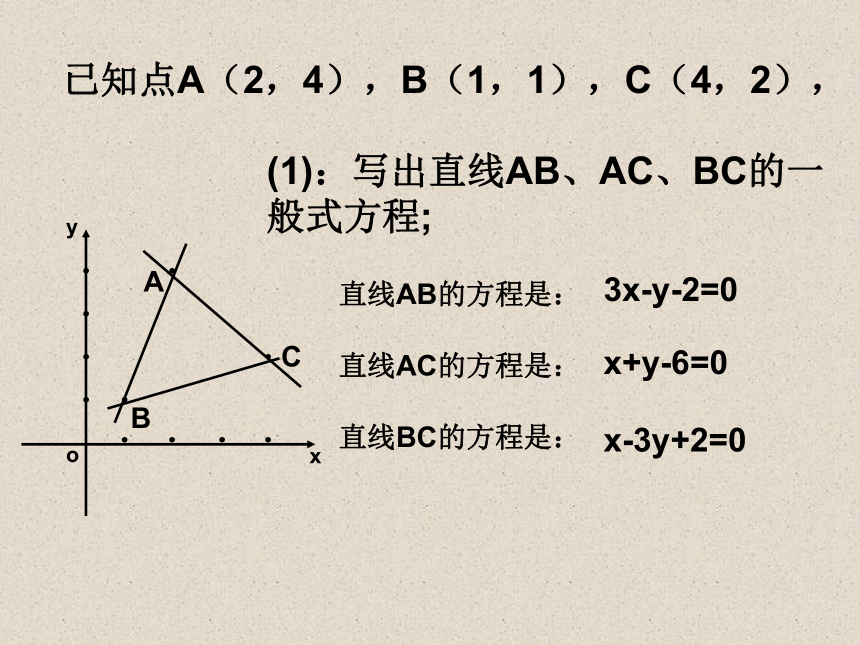
(7)使目标函数达到最大值或最小值的点的坐标,称为问题的最优解. 已知点A(2,4),B(1,1),C(4,2),3x-y-2=0x+y-6=0x-3y+2=0(2):写出由⊿ABC的三条边围成的平面区域的约束条件 (包括三角形的三条边);3x-y-2≥0
x+y-6≤0x-3y+2 ≤ 0问题一:设z=x+2y ,式中的x,y满足约束条件② ,求z的最大值与最小值;...oABC·解:由z=x+2y得,
而 表示直线
在y轴上的截距,画直线 ,
平移直线 ,当其经过
点B时,z最小,经过点A时,z最大.
所以 问题二:设z=2x-y ,式中的x,y满足约束条件② ,求z的最大值与最小值;解:由z=2x-y得,y=2x-z 而-z表示直线 y=2x-z在y轴上的截距,当截距-z最大时, z最小,当截距-z最小时, z最大,画直线y=2x,平移直线y=2x,当其经过点A时,z最小,经过点C时,z最大.
所以 .问题三:设 ,式中的x,y满足约束条件② ,求z的取值范围; .....解:由 即 ,z可以
看做是可行域上的点与原点连线
的斜率,确定边缘线CO,AO.
所以 z的取值范围为(2,4)(1,1)(4,2)问题四:设 ,式中的 x,y满足约束条件② ,求z的最值; 解:由
得
所以z可以看作是可行域上的点到点p
(1,2)的距离的平方,由图像知,
点p到可行域上的点C距离最大,点P
到直线AB的距离d是点P到可行域上
距离最小值。所以P·o问题五:设 ( >0)式中的x,y满足约束条件② ,ⅰ若z取得最大值时有无穷多组最优解,求a的值;
ⅱ若z取得最大值时最优解恰有一个为(4,2),求a的取值范围;
ⅲ若z取得最大值时最优解恰有一个为 (2,4),求a的取值范围.
ⅰ若z取得最大值时有无穷多组最优解,求a的值;
ⅱ若z取得最大值时最优解恰有一个为(4,2),求a的取值范围;
ⅲ若z取得最大值时最优解恰有一个为 (2,4),求a的取值范围;
问题五:设 ( >0)解:(1)由 得 即直线在 轴上的截距最
大时即取 最大值,由图像可知,当直线 与直线AC:x+y-6=0
重合时,最优解有无穷多个。所以
(2)由图像知 , 取最大值时最优解恰有一个为(4,2)则 <-1 又 >0
所以 0< a <2
(3)由图像知 , 取最大值时最优解恰有一个为(2,4) 则 -1< <0
所以 >2小结: 利用线性规划求目标函数最值的步骤
第一步,作图——画出约束条件所确定的平面区域;
第二步,几何意义——将要注意分析目标函数所表示的几何意义,以确定最优解所对应的点的位置;
第三步,求值——解有关方程组求出最优解的坐标,再代入目标函数,求出目标函数的最值.课后探究探究:设z=2x+ay (a<0),式中x、y满足满足约束条件②,求z的最值。 谢谢各位领导及同仁
直线定界,特殊点定域;
若C≠0,则直线定界,原点定域;2、若不等式中不含0,则边界应画成虚线,否则应画成实线。1. 情境引入导学 已知4枝玫瑰与5枝康乃馨的价格之和小于22元,而6枝玫瑰与3枝康乃馨的价格之和大于24元,则2枝玫瑰的价格与3枝康乃馨的价格哪个更高?
2.线性规划的有关概念
(1)把要求最大值或最小值的函数叫做目标函数.
(2)目标函数中的变量所满足的不等式组称为约束条件.
(3)如果目标函数是关于变量的一次函数,则称为线性目标函数.(4)如果约束条件是关于变量的一次不等式(或等式),则称为线性约束条件.
(5)在线性约束条件下,求线性目标函数的最大值或最小值问题,称为线性规划问题.(6)满足线性约束条件的解(x,y)叫做可行解.由所有可行解组成的集合叫做可行域.
(7)使目标函数达到最大值或最小值的点的坐标,称为问题的最优解. 已知点A(2,4),B(1,1),C(4,2),3x-y-2=0x+y-6=0x-3y+2=0(2):写出由⊿ABC的三条边围成的平面区域的约束条件 (包括三角形的三条边);3x-y-2≥0
x+y-6≤0x-3y+2 ≤ 0问题一:设z=x+2y ,式中的x,y满足约束条件② ,求z的最大值与最小值;...oABC·解:由z=x+2y得,
而 表示直线
在y轴上的截距,画直线 ,
平移直线 ,当其经过
点B时,z最小,经过点A时,z最大.
所以 问题二:设z=2x-y ,式中的x,y满足约束条件② ,求z的最大值与最小值;解:由z=2x-y得,y=2x-z 而-z表示直线 y=2x-z在y轴上的截距,当截距-z最大时, z最小,当截距-z最小时, z最大,画直线y=2x,平移直线y=2x,当其经过点A时,z最小,经过点C时,z最大.
所以 .问题三:设 ,式中的x,y满足约束条件② ,求z的取值范围; .....解:由 即 ,z可以
看做是可行域上的点与原点连线
的斜率,确定边缘线CO,AO.
所以 z的取值范围为(2,4)(1,1)(4,2)问题四:设 ,式中的 x,y满足约束条件② ,求z的最值; 解:由
得
所以z可以看作是可行域上的点到点p
(1,2)的距离的平方,由图像知,
点p到可行域上的点C距离最大,点P
到直线AB的距离d是点P到可行域上
距离最小值。所以P·o问题五:设 ( >0)式中的x,y满足约束条件② ,ⅰ若z取得最大值时有无穷多组最优解,求a的值;
ⅱ若z取得最大值时最优解恰有一个为(4,2),求a的取值范围;
ⅲ若z取得最大值时最优解恰有一个为 (2,4),求a的取值范围.
ⅰ若z取得最大值时有无穷多组最优解,求a的值;
ⅱ若z取得最大值时最优解恰有一个为(4,2),求a的取值范围;
ⅲ若z取得最大值时最优解恰有一个为 (2,4),求a的取值范围;
问题五:设 ( >0)解:(1)由 得 即直线在 轴上的截距最
大时即取 最大值,由图像可知,当直线 与直线AC:x+y-6=0
重合时,最优解有无穷多个。所以
(2)由图像知 , 取最大值时最优解恰有一个为(4,2)则 <-1 又 >0
所以 0< a <2
(3)由图像知 , 取最大值时最优解恰有一个为(2,4) 则 -1< <0
所以 >2小结: 利用线性规划求目标函数最值的步骤
第一步,作图——画出约束条件所确定的平面区域;
第二步,几何意义——将要注意分析目标函数所表示的几何意义,以确定最优解所对应的点的位置;
第三步,求值——解有关方程组求出最优解的坐标,再代入目标函数,求出目标函数的最值.课后探究探究:设z=2x+ay (a<0),式中x、y满足满足约束条件②,求z的最值。 谢谢各位领导及同仁
