4.5 相似三角形判定定理的证明 课件(共15张PPT)
文档属性
| 名称 | 4.5 相似三角形判定定理的证明 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 295.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-01 00:00:00 | ||
图片预览


文档简介
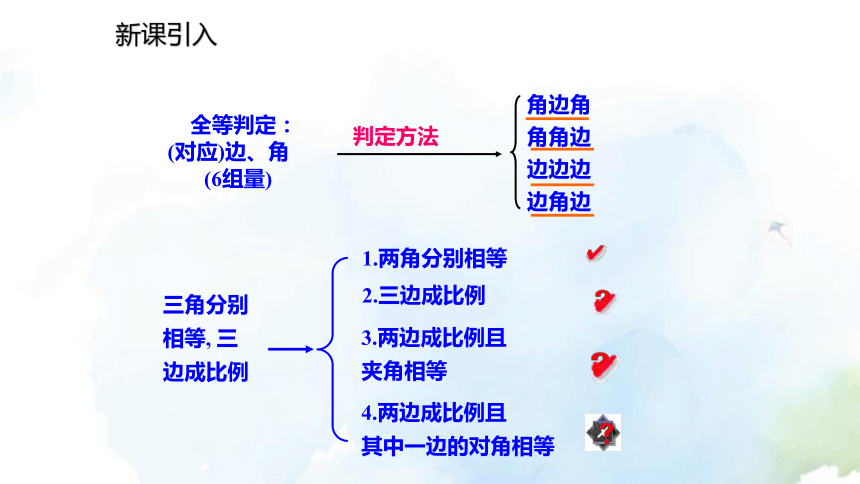
课件15张PPT。九年级数学北师版·上册 相似三角形判定定理第四章图形的相似5 相似三角形判定定理的证明? 两角对应相等,两三角形相似.? 三边对应成比例,两三角形相似.相似三角形的判定方法:? 两边对应成比例且夹角相等,两三角形相似.在上一节中,我们探索了三角形相似的条件,本节我们将对它们进行证明.新课引入
三角分别相等, 三边成比例1.两角分别相等3.两边成比例且
夹角相等2.三边成比例4.两边成比例且
其中一边的对角相等新课引入
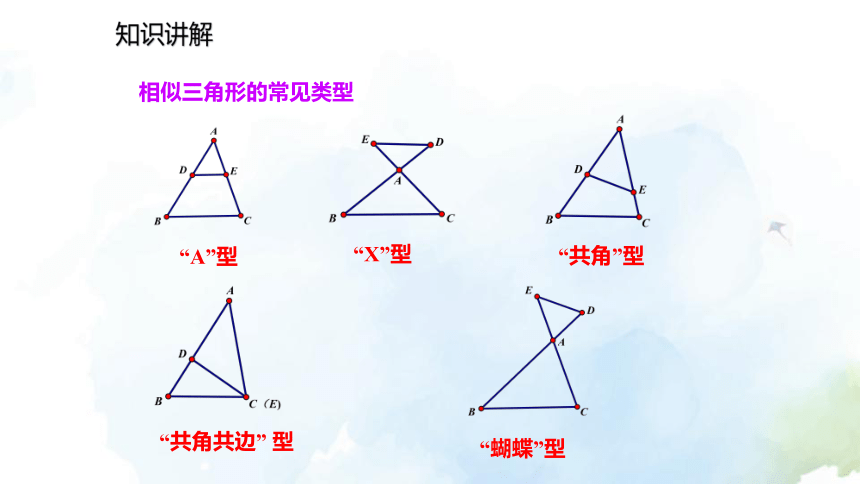
相似三角形的常见类型“A”型“X”型“共角”型“共角共边” 型“蝴蝶”型知识讲解
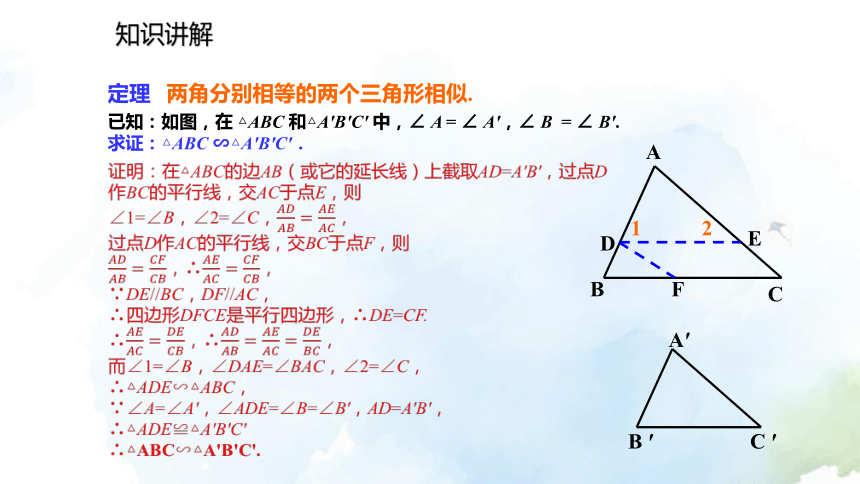
已知:如图,在 △ABC 和△A'B'C' 中,∠ A = ∠ A',∠ B = ∠ B'.
求证:△ABC ∽△A'B'C'.定理 两角分别相等的两个三角形相似.12?知识讲解
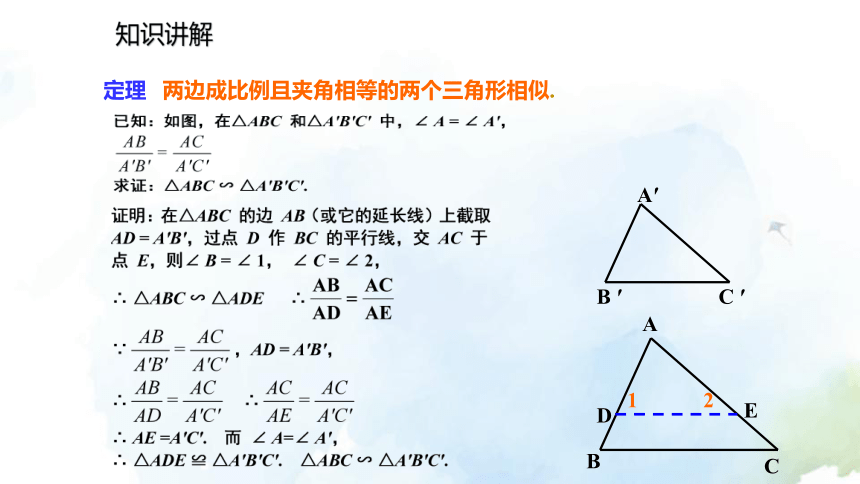
定理 两边成比例且夹角相等的两个三角形相似.12知识讲解
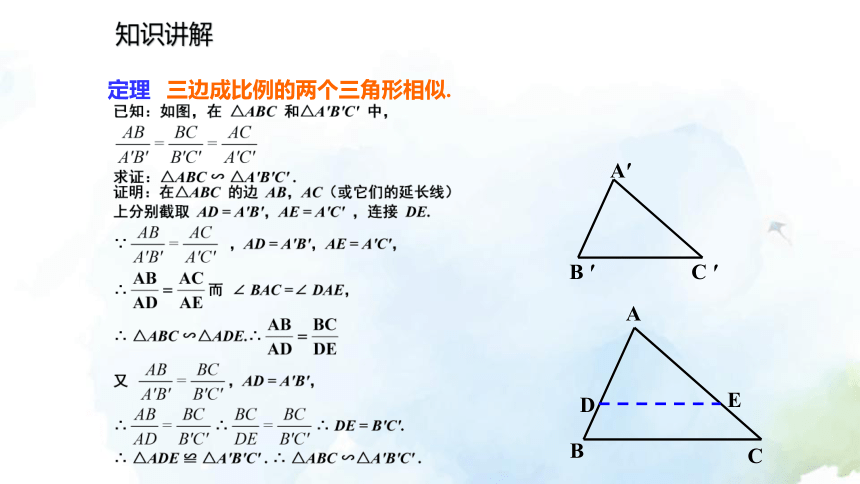
定理 三边成比例的两个三角形相似.知识讲解
解: ∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.已知:如图,∠ABD=∠C,AD=2, AC=8,求AB. 知识讲解
知识点:相似三角形判定定理
1.下列命题中是真命题的是( )
A.有一个角相等的直角三角形都相似
B.有一个角相等的等腰三角形都相似
C.有一个角是120°的等腰三角形都相似
D.两边成比例且有一角相等的三角形都相似C强化训练
2.如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,与BA的延长线交于点F,若AE=2ED,CD=3 cm,则AF的长为( )
A.5 cm B.6 cm C.7 cm D.8 cmB强化训练
? 两角对应相等,两三角形相似.? 三边对应成比例,两三角形相似.相似三角形的判定方法:? 两边对应成比例且夹角相等,两三角形相似.课堂总结
1.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个B目标测试
2.如图,在?ABCD中,AB=10,AD=6,点E是边AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是_______.1.8目标测试
∠ACB=∠BCD∴△ABC∽△BDC(两边成比例且夹角相等的两个三角形相似)∴∠ABC=∠CDB(2)∵△ABC∽△BDC∴AC·BD=BC·AB目标测试
谢 谢
三角分别相等, 三边成比例1.两角分别相等3.两边成比例且
夹角相等2.三边成比例4.两边成比例且
其中一边的对角相等新课引入
相似三角形的常见类型“A”型“X”型“共角”型“共角共边” 型“蝴蝶”型知识讲解
已知:如图,在 △ABC 和△A'B'C' 中,∠ A = ∠ A',∠ B = ∠ B'.
求证:△ABC ∽△A'B'C'.定理 两角分别相等的两个三角形相似.12?知识讲解
定理 两边成比例且夹角相等的两个三角形相似.12知识讲解
定理 三边成比例的两个三角形相似.知识讲解
解: ∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.已知:如图,∠ABD=∠C,AD=2, AC=8,求AB. 知识讲解
知识点:相似三角形判定定理
1.下列命题中是真命题的是( )
A.有一个角相等的直角三角形都相似
B.有一个角相等的等腰三角形都相似
C.有一个角是120°的等腰三角形都相似
D.两边成比例且有一角相等的三角形都相似C强化训练
2.如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,与BA的延长线交于点F,若AE=2ED,CD=3 cm,则AF的长为( )
A.5 cm B.6 cm C.7 cm D.8 cmB强化训练
? 两角对应相等,两三角形相似.? 三边对应成比例,两三角形相似.相似三角形的判定方法:? 两边对应成比例且夹角相等,两三角形相似.课堂总结
1.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个B目标测试
2.如图,在?ABCD中,AB=10,AD=6,点E是边AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是_______.1.8目标测试
∠ACB=∠BCD∴△ABC∽△BDC(两边成比例且夹角相等的两个三角形相似)∴∠ABC=∠CDB(2)∵△ABC∽△BDC∴AC·BD=BC·AB目标测试
谢 谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
