6.1 反比例函数 课件(14张PPT)
文档属性
| 名称 | 6.1 反比例函数 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-01 00:00:00 | ||
图片预览





文档简介
课件14张PPT。第六章 反比例函数6.1 反比例函数一、新课引入
一次函数若两个变量x,y的关系可以表示y=kx+b(k,b是常数,k≠0)的形式,则称y是x的一次函数 (x为自变量,y为因变量).
特别地,当常数b=0时,一次函数y=kx+b(k≠0)就成为:y=kx(k是常数,k≠0),称y是x的正比例函数.一次函数与正比例函数之间的关系:
正比例函数是特殊的一次函数. “函数” 知多少一、新课引入
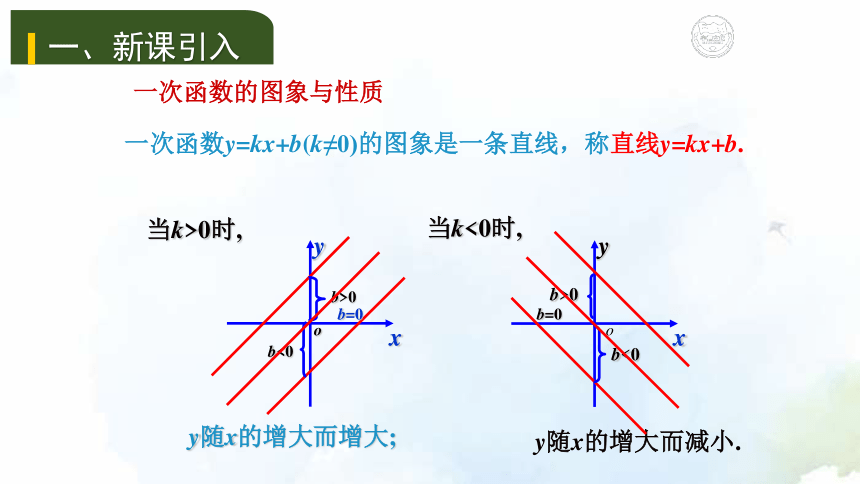
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.y随x的增大而增大;一次函数的图象与性质y随x的增大而减小.b=0b=0当k>0时,当k<0时,二、新课讲解
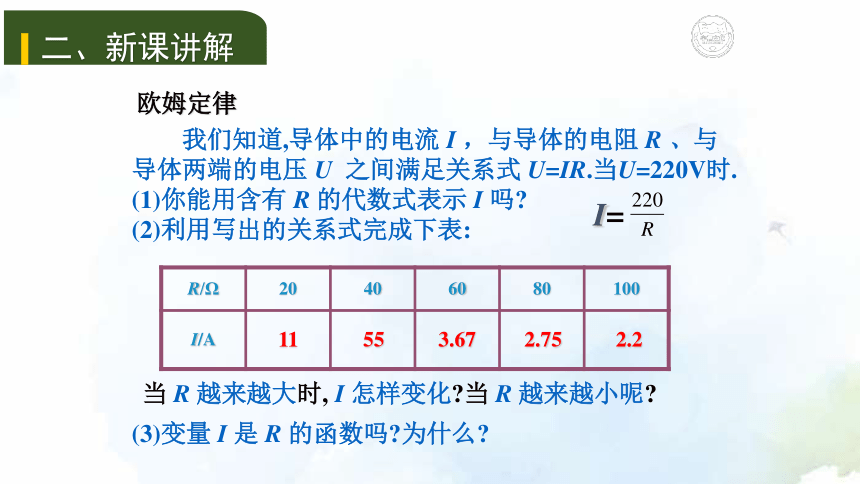
欧姆定律 我们知道,导体中的电流 I ,与导体的电阻 R 、与导体两端的电压 U 之间满足关系式 U=IR.当U=220V时.
(1)你能用含有 R 的代数式表示 I 吗?
(2)利用写出的关系式完成下表:当 R 越来越大时, I 怎样变化?当 R 越来越小呢? 11 55 3.67 2.75 2.2(3)变量 I 是 R 的函数吗?为什么?I=二、新课讲解
行程问题中的函数关系 京沪高速铁路全长约为1318 km ,列车沿京沪高速铁路从上海驶往北京,列车行完全程所需的时间 t (h)与行驶的平均速度 v (km/h)之间有怎样的关系?变量 t 是 v 的函数吗?为什么?变量 t 与 v 之间的关系可表示为:t=二、新课讲解
以下函数解析式哪些是一次函数?其余函数解析式有什么异同?(1)y=3x(2)y=0.7x-2(3)y= x+2(4)I=(5)t=(4)(5)的相同之处:
①均为两个变量之间的一一对应关系;
②均为一变量等于另一变量倒数的常数倍,即右边分子为一个常数. 一般地,如果两个变量x、y之间的对应关系可以表示成 (k为常数,k ≠0)的形式,那么称y是x的反比例函数.y= 想一想,此式子中的x能为0吗?反比例函数还有哪些表示形式?答案:(1)(2)(3)为一次函数二、新课讲解
2、某村有耕地 346.2 hm2,人口数量 n 逐年发生变化,那么该村人均占有耕地面积 m (hm2/人)是全村人口数 n 的函数吗?是反比例函数吗?为什么?1、一个矩形的面积为 20 cm2,相邻的两条边长分别为 x cm 和 y cm,那么变量 y 是变量 x 的函数吗?是反比例函数吗?为什么?m=二、新课讲解
确定反比例函数的解析式(1)写出这个反比例函数的表达式;3、 y 是 x 的反比例函数,下表给出了 x 与 y 的一些值.(2)根据函数表达式完成上表.-314-4-22-2/3三、归纳小结
1.一次函数的定义;
若两个变量 x ,y 的关系可以表示 y=kx+b ( k , b 是常数, k ≠ 0 )的形式,则称 y 是 x 的一次函数 ( x 为自变量, y 为因变量).
2.正比例函数的定义;
当常数 b = 0 时,一次函数 y=kx+b ( k ≠ 0 )就成为: y=kx ( k 是常数, k ≠ 0 ),称 y 是 x 的正比例函数.
关系: 正比例函数是特殊的一次函数.
3.反比例函数的定义.
一般地,如果两个变量 x ,y 之间的对应关系可以表示成 y = ( k 为常数,k ≠ 0 )的形式,那么称 y 是 x 的反比例函数.四、强化训练
1.若 y =-3xa+1是反比例函数,则a=_.-2解:∵y =-3xa+1是反比例函数,
∴a+1=-1,
∴a=-2.02.若 y =(a+2)x 为反比例函数关系式,则a=_.解:∵y =(a+2)x 为反比例函数,
∴a+2≠0且a2+2a-1=0,
∴a=0.四、强化训练
3.ⅰ)当路程 s 一定时,时间 t 与速度 v 的函数关系
ⅱ)当矩形面积 s 一定时,长 a 与宽 b 的函数关系
ⅲ)当三角形面积 s 一定时,三角形的底边 y 与高 x
的函数关系
四、强化训练
4.用 x 表示自变量,y 表示 x 的函数,下列给出的函数关系中,是反比列函数关系的是( )
A .长方形的周长为 2,长为 x,宽为 y
B .正方形的边长为 x,面积为 y
C .李明以 2 米/秒的速度行走,行走的时间 x,行走的路程 y
D .王芳以 x 米/分钟的速度花 y 分钟爬完 40 米的高楼D四、强化训练
5.生活中有许多反比列函数的例子,在下面的实例中,x 和 y 成反比例函数关系的有几个? ( )
(1)x 人共饮水 10 kg,平均每人饮水 y kg
(2)底面半径为 x m,高为 y m的圆柱形水桶的体积为π m3
(3)用铁丝做一个圆,铁丝的长为 x cm,做成圆的半径为 y cm
(4)在水龙头前放满一桶水,出水的速度为 x ,放满一桶水的时间 y
A.1个 B.2个 C.3个 D.4个B本课结束
一次函数若两个变量x,y的关系可以表示y=kx+b(k,b是常数,k≠0)的形式,则称y是x的一次函数 (x为自变量,y为因变量).
特别地,当常数b=0时,一次函数y=kx+b(k≠0)就成为:y=kx(k是常数,k≠0),称y是x的正比例函数.一次函数与正比例函数之间的关系:
正比例函数是特殊的一次函数. “函数” 知多少一、新课引入
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.y随x的增大而增大;一次函数的图象与性质y随x的增大而减小.b=0b=0当k>0时,当k<0时,二、新课讲解
欧姆定律 我们知道,导体中的电流 I ,与导体的电阻 R 、与导体两端的电压 U 之间满足关系式 U=IR.当U=220V时.
(1)你能用含有 R 的代数式表示 I 吗?
(2)利用写出的关系式完成下表:当 R 越来越大时, I 怎样变化?当 R 越来越小呢? 11 55 3.67 2.75 2.2(3)变量 I 是 R 的函数吗?为什么?I=二、新课讲解
行程问题中的函数关系 京沪高速铁路全长约为1318 km ,列车沿京沪高速铁路从上海驶往北京,列车行完全程所需的时间 t (h)与行驶的平均速度 v (km/h)之间有怎样的关系?变量 t 是 v 的函数吗?为什么?变量 t 与 v 之间的关系可表示为:t=二、新课讲解
以下函数解析式哪些是一次函数?其余函数解析式有什么异同?(1)y=3x(2)y=0.7x-2(3)y= x+2(4)I=(5)t=(4)(5)的相同之处:
①均为两个变量之间的一一对应关系;
②均为一变量等于另一变量倒数的常数倍,即右边分子为一个常数. 一般地,如果两个变量x、y之间的对应关系可以表示成 (k为常数,k ≠0)的形式,那么称y是x的反比例函数.y= 想一想,此式子中的x能为0吗?反比例函数还有哪些表示形式?答案:(1)(2)(3)为一次函数二、新课讲解
2、某村有耕地 346.2 hm2,人口数量 n 逐年发生变化,那么该村人均占有耕地面积 m (hm2/人)是全村人口数 n 的函数吗?是反比例函数吗?为什么?1、一个矩形的面积为 20 cm2,相邻的两条边长分别为 x cm 和 y cm,那么变量 y 是变量 x 的函数吗?是反比例函数吗?为什么?m=二、新课讲解
确定反比例函数的解析式(1)写出这个反比例函数的表达式;3、 y 是 x 的反比例函数,下表给出了 x 与 y 的一些值.(2)根据函数表达式完成上表.-314-4-22-2/3三、归纳小结
1.一次函数的定义;
若两个变量 x ,y 的关系可以表示 y=kx+b ( k , b 是常数, k ≠ 0 )的形式,则称 y 是 x 的一次函数 ( x 为自变量, y 为因变量).
2.正比例函数的定义;
当常数 b = 0 时,一次函数 y=kx+b ( k ≠ 0 )就成为: y=kx ( k 是常数, k ≠ 0 ),称 y 是 x 的正比例函数.
关系: 正比例函数是特殊的一次函数.
3.反比例函数的定义.
一般地,如果两个变量 x ,y 之间的对应关系可以表示成 y = ( k 为常数,k ≠ 0 )的形式,那么称 y 是 x 的反比例函数.四、强化训练
1.若 y =-3xa+1是反比例函数,则a=_.-2解:∵y =-3xa+1是反比例函数,
∴a+1=-1,
∴a=-2.02.若 y =(a+2)x 为反比例函数关系式,则a=_.解:∵y =(a+2)x 为反比例函数,
∴a+2≠0且a2+2a-1=0,
∴a=0.四、强化训练
3.ⅰ)当路程 s 一定时,时间 t 与速度 v 的函数关系
ⅱ)当矩形面积 s 一定时,长 a 与宽 b 的函数关系
ⅲ)当三角形面积 s 一定时,三角形的底边 y 与高 x
的函数关系
四、强化训练
4.用 x 表示自变量,y 表示 x 的函数,下列给出的函数关系中,是反比列函数关系的是( )
A .长方形的周长为 2,长为 x,宽为 y
B .正方形的边长为 x,面积为 y
C .李明以 2 米/秒的速度行走,行走的时间 x,行走的路程 y
D .王芳以 x 米/分钟的速度花 y 分钟爬完 40 米的高楼D四、强化训练
5.生活中有许多反比列函数的例子,在下面的实例中,x 和 y 成反比例函数关系的有几个? ( )
(1)x 人共饮水 10 kg,平均每人饮水 y kg
(2)底面半径为 x m,高为 y m的圆柱形水桶的体积为π m3
(3)用铁丝做一个圆,铁丝的长为 x cm,做成圆的半径为 y cm
(4)在水龙头前放满一桶水,出水的速度为 x ,放满一桶水的时间 y
A.1个 B.2个 C.3个 D.4个B本课结束
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
