2.2等差数列(第一课时) 课件(21张PPT)
文档属性
| 名称 | 2.2等差数列(第一课时) 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 00:00:00 | ||
图片预览








文档简介
课件21张PPT。必修5 2.2 等差数列
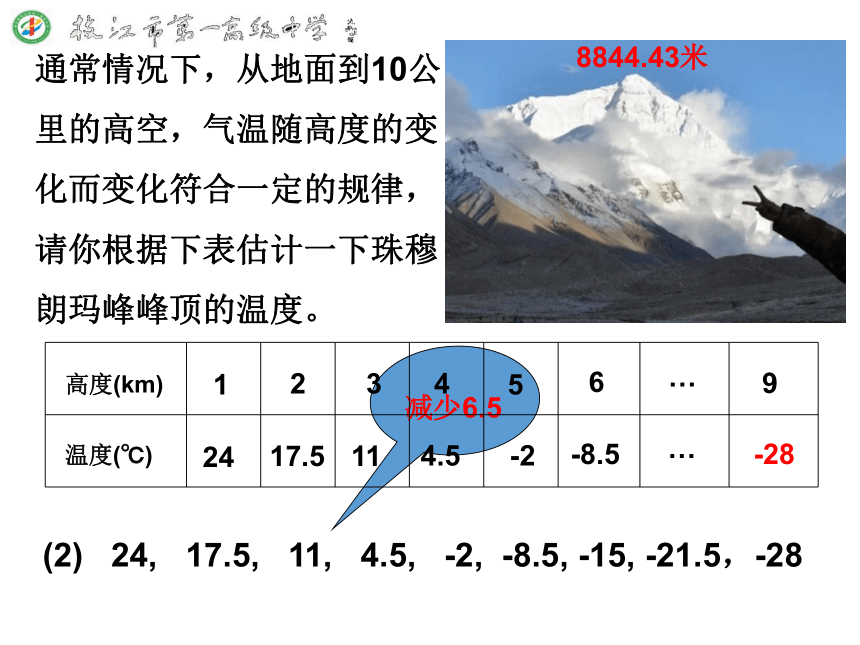
第1课时 (1)1682,1758,1834,1910,1986,( )2062在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星相差76情景设置,激活经验-28(2) 24, 17.5, 11, 4.5, -2, -8.5, -15, -21.5,-28数列21682,1758,1834,1910,1986,…
数列1 24, 17.5, 11, 4.5, -2, -8.5, … 共同特点:
从第2项起,每一项与其前一项的差都等于同一个常数.观察思考,经验激活上面的数列有什么共同的特点?数列3 2, 2, 2, 2, 2, 2,2 …
1、等差数列的概念一般地,如果一个数列从______起,每一项与它的前一
项的差等于__________,那么这个数列就叫做等差数列,这个常数叫做等差数列的______,公差常用字母d表示。二、新知概念,经验感悟第2项同一个常数公差请用数学语言描述等差数列的定义等差数列定义注意练1、请同学们说出活动1中三个等差数列的公差为多少?
(1)d=_____ (2)d=_____ (3)d=_____练2、下列数列是等差数列吗?为什么?
(1)4,7,10,13,16, ,23…
(2) , 3, 5, 7, 9,11,13…
(3)6,6,6,6,6,6,…76-6.5019,202分析:由等差数列的定义得①利用等差数列定义可以证明和判断一个数列是否是等差数列。引导学生从论证推理、抽象过程中获得经验2、等差数列的通项公式-10-13分析:根据等差数列的定义得到不完全
归纳法等差数列的通项公式的推导n≥2将所有等式左右两边分别相加得法二:累加法等差数列的通项公式的推导学生活动3学生活动4中动手操作,经验重构分析:经验生成:等差数列通项公式的推广形式 (1)在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:(1)2 ,( ) , 4 (2)-12,( ) ,0 3-6 (2)等差中项的定义: 如果在a与b中间插入一个数A,使 a,A,b成等差数列,那么A叫做a与b的等差中项。( 3 ) , ( ) , 3、等差中项3、等差中项经验生成:等差中项法也可以用来证明判断一个数列是等差数列三、例题讲解,经验内化分析:解:
由等差数列通项公式得:解之得n=100,即-401是这个数列的第100项。引导学生从动手操作、实践过程中获得经验解:
由等差数列通项公式得:三、例题讲解,经验内化引导学生从动手操作、实践过程中获得经验例题讲解,经验内化解:由题意得解得法一法二解:由题意得1.等差数列的定义:
an-an-1=d (n≥2)或 an+1-an=d (n∈N*) 2. 等差数列的通项公式
an =a1+(n-1)d = am+(n-m)d3.等差中项(k、常数)课堂小结,经验升华巩固练习1.等差数列{an}的前三项依次为 a-6,-3a-5,-10a-1,
则 a = 1 .
2. 在数列{an}中a1=1,an= an+1+4,则a10= .(-3a-5 )-(a-6)=(-10a-1) -(-3a-5 )提示:提示:d=an+1- an=-4-353.第15届现代奥运会于1952年在芬兰赫尔辛基举行,每4年举行一次。奥运会如因故不能举行,届数照算。
(1)试写出由举行奥运会的年份构成的数列的通项公式。
(2)2008年北京奥运会是第几届?
(3)2050年举行奥运会吗?
谢谢聆听!
第1课时 (1)1682,1758,1834,1910,1986,( )2062在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星相差76情景设置,激活经验-28(2) 24, 17.5, 11, 4.5, -2, -8.5, -15, -21.5,-28数列21682,1758,1834,1910,1986,…
数列1 24, 17.5, 11, 4.5, -2, -8.5, … 共同特点:
从第2项起,每一项与其前一项的差都等于同一个常数.观察思考,经验激活上面的数列有什么共同的特点?数列3 2, 2, 2, 2, 2, 2,2 …
1、等差数列的概念一般地,如果一个数列从______起,每一项与它的前一
项的差等于__________,那么这个数列就叫做等差数列,这个常数叫做等差数列的______,公差常用字母d表示。二、新知概念,经验感悟第2项同一个常数公差请用数学语言描述等差数列的定义等差数列定义注意练1、请同学们说出活动1中三个等差数列的公差为多少?
(1)d=_____ (2)d=_____ (3)d=_____练2、下列数列是等差数列吗?为什么?
(1)4,7,10,13,16, ,23…
(2) , 3, 5, 7, 9,11,13…
(3)6,6,6,6,6,6,…76-6.5019,202分析:由等差数列的定义得①利用等差数列定义可以证明和判断一个数列是否是等差数列。引导学生从论证推理、抽象过程中获得经验2、等差数列的通项公式-10-13分析:根据等差数列的定义得到不完全
归纳法等差数列的通项公式的推导n≥2将所有等式左右两边分别相加得法二:累加法等差数列的通项公式的推导学生活动3学生活动4中动手操作,经验重构分析:经验生成:等差数列通项公式的推广形式 (1)在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:(1)2 ,( ) , 4 (2)-12,( ) ,0 3-6 (2)等差中项的定义: 如果在a与b中间插入一个数A,使 a,A,b成等差数列,那么A叫做a与b的等差中项。( 3 ) , ( ) , 3、等差中项3、等差中项经验生成:等差中项法也可以用来证明判断一个数列是等差数列三、例题讲解,经验内化分析:解:
由等差数列通项公式得:解之得n=100,即-401是这个数列的第100项。引导学生从动手操作、实践过程中获得经验解:
由等差数列通项公式得:三、例题讲解,经验内化引导学生从动手操作、实践过程中获得经验例题讲解,经验内化解:由题意得解得法一法二解:由题意得1.等差数列的定义:
an-an-1=d (n≥2)或 an+1-an=d (n∈N*) 2. 等差数列的通项公式
an =a1+(n-1)d = am+(n-m)d3.等差中项(k、常数)课堂小结,经验升华巩固练习1.等差数列{an}的前三项依次为 a-6,-3a-5,-10a-1,
则 a = 1 .
2. 在数列{an}中a1=1,an= an+1+4,则a10= .(-3a-5 )-(a-6)=(-10a-1) -(-3a-5 )提示:提示:d=an+1- an=-4-353.第15届现代奥运会于1952年在芬兰赫尔辛基举行,每4年举行一次。奥运会如因故不能举行,届数照算。
(1)试写出由举行奥运会的年份构成的数列的通项公式。
(2)2008年北京奥运会是第几届?
(3)2050年举行奥运会吗?
谢谢聆听!
