2.2等差数列 课件(25张PPT)
文档属性
| 名称 | 2.2等差数列 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 00:00:00 | ||
图片预览








文档简介
课件25张PPT。
2.2.1 等差数列问题情景一我们经常这样数数,从0开始,每隔5数一次,可以得到一个数列:0,5,10,15,20,25,……得到数列:
6000,6500,7000,7500,
8000,8500,9000
问题情景二 匡威运动鞋(女)的尺码(鞋底长,单位是cm)问题情景三 ,23,,24,25,,26,,26 姚明罚球个数的数列:
6000,6500,7000,7500,8000,8500,9000发现?观察:以上数列有什么共同特点?从第 2项起,每一项与前一项的差都等于同一常数。数数得到的数列:
0,5,10,15,20,25,……观察 归纳 运动鞋尺码的数列 一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列。这个常数叫做等差数列的公差,通常用字母d表示。 等差数列定义如果在a与b的中间插入一个数A,使a, A, b成等差数列,那么A应该满足什么条件?
开动脑筋由定义得:反之,若 则所以 a, A, b成等差数列等差中项: 若三个数a,A,b组成等差数列,则A叫做a与
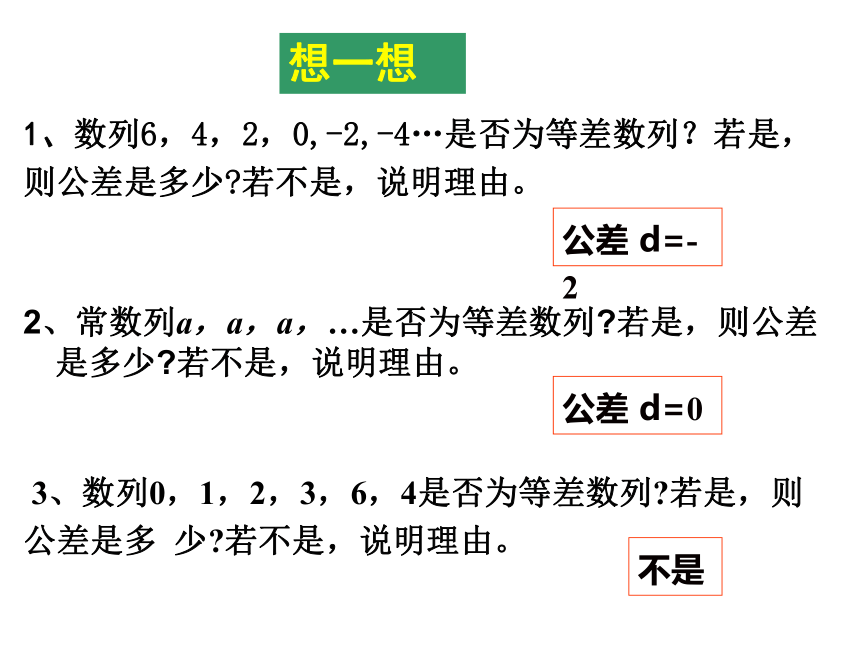
b的等差中项. 不难发现,在一个等差数列中,从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项. 2、常数列a,a,a,…是否为等差数列?若是,则公差是多少?若不是,说明理由。 想一想公差 d=0 3、数列0,1,2,3,6,4是否为等差数列?若是,则公差是多 少?若不是,说明理由。不是1、数列6,4,2,0,-2,-4…是否为等差数列?若是,则公差是多少?若不是,说明理由。 公差 d=-2练习: 已知等差数列的首项为12,公差为-5,试写出这个数列的第2项到第5项. 解: 由于,因此 概念强化 由定义知:
a2-a1=d,即:a2=a1+d,
a3-a2=d,即:a3=a2+d = (a1+d) + d = a1+ 2d
a4-a3=d,即:a4=a3+d =(a1+2d)+d = a1+3d
……
由此归纳出等差数列的通项公式为: an=a1+(n-1)d若已知等差数列{an}的首项是a1,公差是d,你能根据等差数列的定义推导出等差数列的通项公式吗?探究 等差数列通项公式 n=1时亦适合叠加得…共n-1个式子探究 等差数列通项公式?探究 等差数列通项公式等差数列的通项公式:首项为a1 ,公差为d的等差数列
{an}的通项公式:an = a1 + (n-1)d a1 、an、n、d知三求一也就是说,在数列计算题中要注意运用方程思想。通项公式与方程例1 (1) 求等差数列8,5,2,…,的第20项。解:(2) 等差数列 -5,-9,-13,…,的第几项是 –401?解:因此,解得例2 在等差数列中,已知a5=10,a12=31,解:由题意可知 这是一个以 和 为未知数的二元一次方程组,解这个方程组,得即这个等差数列的首项是-2,公差是3.求首项a1与公差d.1. 求等差数列3,7,11,…的第 7,10项;2. 100是不是等差数列2,9,16,…中的项?3. -20是不是等差数列0,- ,….- 7…中的项;练一练练一练4. 在等差数列中已知数列 的通项公式是 ( 为常数)那么这个数列为等差数列吗?等差数列与一次函数的关系解:
它是一个与 无关的数。所以 是等差数列。以 为公差, 为首项。
探究:等差数列的图象1(1)数列:-2,0,2,4,6,8,10,…●●●●●●●等差数列的图象2(2)数列:7,4,1,-2,…●●●●等差数列的图象3(3)数列:4,4,4,4,4,4,4,…●●●●●●●●●●2.d>0,图像上升,函数是增函数,数列是递增数列;
d<0,图像下降,函数是减函数,数列是递减数列;
d=0,图像平行于X轴,函数是常函数,数列是常数列等差数列的图象课堂小结1.本节课学习的主要内容有2.本节课的能力要求3.思想方法
6000,6500,7000,7500,
8000,8500,9000
问题情景二 匡威运动鞋(女)的尺码(鞋底长,单位是cm)问题情景三 ,23,,24,25,,26,,26 姚明罚球个数的数列:
6000,6500,7000,7500,8000,8500,9000发现?观察:以上数列有什么共同特点?从第 2项起,每一项与前一项的差都等于同一常数。数数得到的数列:
0,5,10,15,20,25,……观察 归纳 运动鞋尺码的数列 一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列。这个常数叫做等差数列的公差,通常用字母d表示。 等差数列定义如果在a与b的中间插入一个数A,使a, A, b成等差数列,那么A应该满足什么条件?
开动脑筋由定义得:反之,若 则所以 a, A, b成等差数列等差中项: 若三个数a,A,b组成等差数列,则A叫做a与
b的等差中项. 不难发现,在一个等差数列中,从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项. 2、常数列a,a,a,…是否为等差数列?若是,则公差是多少?若不是,说明理由。 想一想公差 d=0 3、数列0,1,2,3,6,4是否为等差数列?若是,则公差是多 少?若不是,说明理由。不是1、数列6,4,2,0,-2,-4…是否为等差数列?若是,则公差是多少?若不是,说明理由。 公差 d=-2练习: 已知等差数列的首项为12,公差为-5,试写出这个数列的第2项到第5项. 解: 由于,因此 概念强化 由定义知:
a2-a1=d,即:a2=a1+d,
a3-a2=d,即:a3=a2+d = (a1+d) + d = a1+ 2d
a4-a3=d,即:a4=a3+d =(a1+2d)+d = a1+3d
……
由此归纳出等差数列的通项公式为: an=a1+(n-1)d若已知等差数列{an}的首项是a1,公差是d,你能根据等差数列的定义推导出等差数列的通项公式吗?探究 等差数列通项公式 n=1时亦适合叠加得…共n-1个式子探究 等差数列通项公式?探究 等差数列通项公式等差数列的通项公式:首项为a1 ,公差为d的等差数列
{an}的通项公式:an = a1 + (n-1)d a1 、an、n、d知三求一也就是说,在数列计算题中要注意运用方程思想。通项公式与方程例1 (1) 求等差数列8,5,2,…,的第20项。解:(2) 等差数列 -5,-9,-13,…,的第几项是 –401?解:因此,解得例2 在等差数列中,已知a5=10,a12=31,解:由题意可知 这是一个以 和 为未知数的二元一次方程组,解这个方程组,得即这个等差数列的首项是-2,公差是3.求首项a1与公差d.1. 求等差数列3,7,11,…的第 7,10项;2. 100是不是等差数列2,9,16,…中的项?3. -20是不是等差数列0,- ,….- 7…中的项;练一练练一练4. 在等差数列中已知数列 的通项公式是 ( 为常数)那么这个数列为等差数列吗?等差数列与一次函数的关系解:
它是一个与 无关的数。所以 是等差数列。以 为公差, 为首项。
探究:等差数列的图象1(1)数列:-2,0,2,4,6,8,10,…●●●●●●●等差数列的图象2(2)数列:7,4,1,-2,…●●●●等差数列的图象3(3)数列:4,4,4,4,4,4,4,…●●●●●●●●●●2.d>0,图像上升,函数是增函数,数列是递增数列;
d<0,图像下降,函数是减函数,数列是递减数列;
d=0,图像平行于X轴,函数是常函数,数列是常数列等差数列的图象课堂小结1.本节课学习的主要内容有2.本节课的能力要求3.思想方法
