3.5.2 简单线性规划 课件(23张PPT)
文档属性
| 名称 | 3.5.2 简单线性规划 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 00:00:00 | ||
图片预览







文档简介
课件23张PPT。普通高中课程标准实验教科书 必修5第三章《不等式》
(人民教育出版社)A版 3.3.2简单的线性规划问题3.3.2简单的线性规划问题学习目标:
1.理解线性规划有关概念(约束条件、目标函数、可行解、可行域、最优解等);
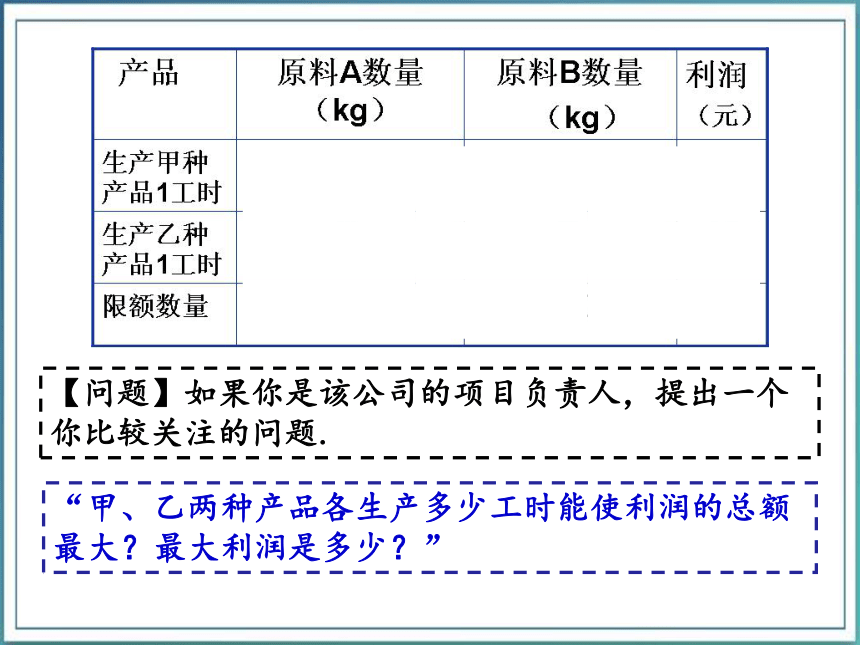
2.初步学会解决简单的线性规划问题. 位于新疆克拉玛依市的中国石油公司为开拓市场,深度开发原油,计划生产甲、乙两种产品.这两种产品都需要两种石油原料,生产甲产品1工时需要A种原料3kg,B种原料1kg;生产乙产品1工时需要A种原料2kg,B种原料2kg.现有A种原料1200kg,B种原料800kg.生产甲产品每工时的利润是30元,生产乙产品每工时的平均利润是40元.【问题】如果你是该公司的项目负责人,提出一个你比较关注的问题.“甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?” 设计划生产甲种产品x工时,生产乙种产品y工时,获得利润总额为Z.线性约束条件线性目标函数决策变量x,y有序实数对(x,y)代数问题平面直角坐标系可行域可行解(x,y)
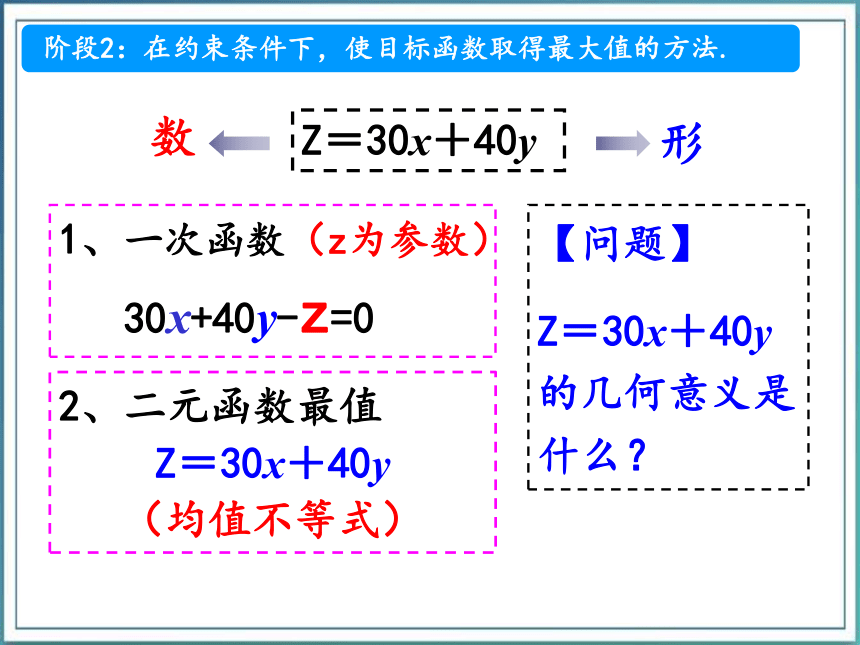
Z=30x+40y 数形1、一次函数(z为参数)
30x+40y-z=02、二元函数最值
Z=30x+40y
(均值不等式)【问题】
Z=30x+40y的几何意义是什么? 【反思】是否直线在y轴上的截距越大,Z的值就越大? Z=30x+40y 直线的方程 0=30x+40y Z=30x+40y 特殊一般直线直线系最优解所对应的点就是在可行域内到直线距离最大的点. 【问题】表示平面区域内任意一点P(x,y)到直线30x+40y=0的距离d .z 在线性约束条件下,求线性目标函数的最大值或最小值的问题,称为线性规划问题.数形结合与直线在y轴上的截距的联系,平移直线. 与点到直线的距离的联系,运动点. 1.建3.移4.求5.答 新疆和田玉石加工厂用A、B两种石料生产优质套装、精品套装两种产品,其生产情况如下, 请解读上述表格,试问:该厂所有可能的日生产安排是什么?(1)用不等式组表示问题中的限制条件: 设产品优质套装x件、精品套装y件,由已知条件可得二元一次不等式组:(2)画出不等式组所表示的平面区域: 如图,图中的阴影部分的整点(坐标为整数的点)就代表所有可能的日生产安排. yx320x +2 y-8 = 01412348(3)提出新问题:进一步,若生产一件优质套装获利2万元,生产一件精品套装获利3万元,采用哪种生产安排利润最大?设工厂生产优质套装x件,生产精品套装y件,获得利润为Z,则Z = 2x + 3y,求Z的最大值. (4)尝试解答
1 (4)尝试解答
2 (5)获得结果: 答:每天生产优质套装4件,精品套装2件时,工厂可获得最大利润14万元. (6)课后思考思考1:在上述问题中,若生产一件优质套装获利3万元,生产一件精品套装获利2万元,又当如何安排生产才能获得最大利润?
思考2:在上述问题中,若生产一件优质套装获利1万元,生产一件精品套装获利2万元,又当如何安排生产才能获得最大利润?知识方法思想线性规划的相关概念
解决线性规划问题步骤:建、画、移、求、答.(1)将目标函数值与直线在y轴上的截距相联系;
(2)将目标函数值与点到直线的距离相联系;
(3)代入法;数形结合、转化,从特殊到一般 函数线性规划定义域可行域函数目标函数最值最优化自变量可行解二元函数的最值问题均值不等式线性规划单元小结谢谢各位老师指导
(人民教育出版社)A版 3.3.2简单的线性规划问题3.3.2简单的线性规划问题学习目标:
1.理解线性规划有关概念(约束条件、目标函数、可行解、可行域、最优解等);
2.初步学会解决简单的线性规划问题. 位于新疆克拉玛依市的中国石油公司为开拓市场,深度开发原油,计划生产甲、乙两种产品.这两种产品都需要两种石油原料,生产甲产品1工时需要A种原料3kg,B种原料1kg;生产乙产品1工时需要A种原料2kg,B种原料2kg.现有A种原料1200kg,B种原料800kg.生产甲产品每工时的利润是30元,生产乙产品每工时的平均利润是40元.【问题】如果你是该公司的项目负责人,提出一个你比较关注的问题.“甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?” 设计划生产甲种产品x工时,生产乙种产品y工时,获得利润总额为Z.线性约束条件线性目标函数决策变量x,y有序实数对(x,y)代数问题平面直角坐标系可行域可行解(x,y)
Z=30x+40y 数形1、一次函数(z为参数)
30x+40y-z=02、二元函数最值
Z=30x+40y
(均值不等式)【问题】
Z=30x+40y的几何意义是什么? 【反思】是否直线在y轴上的截距越大,Z的值就越大? Z=30x+40y 直线的方程 0=30x+40y Z=30x+40y 特殊一般直线直线系最优解所对应的点就是在可行域内到直线距离最大的点. 【问题】表示平面区域内任意一点P(x,y)到直线30x+40y=0的距离d .z 在线性约束条件下,求线性目标函数的最大值或最小值的问题,称为线性规划问题.数形结合与直线在y轴上的截距的联系,平移直线. 与点到直线的距离的联系,运动点. 1.建3.移4.求5.答 新疆和田玉石加工厂用A、B两种石料生产优质套装、精品套装两种产品,其生产情况如下, 请解读上述表格,试问:该厂所有可能的日生产安排是什么?(1)用不等式组表示问题中的限制条件: 设产品优质套装x件、精品套装y件,由已知条件可得二元一次不等式组:(2)画出不等式组所表示的平面区域: 如图,图中的阴影部分的整点(坐标为整数的点)就代表所有可能的日生产安排. yx320x +2 y-8 = 01412348(3)提出新问题:进一步,若生产一件优质套装获利2万元,生产一件精品套装获利3万元,采用哪种生产安排利润最大?设工厂生产优质套装x件,生产精品套装y件,获得利润为Z,则Z = 2x + 3y,求Z的最大值. (4)尝试解答
1 (4)尝试解答
2 (5)获得结果: 答:每天生产优质套装4件,精品套装2件时,工厂可获得最大利润14万元. (6)课后思考思考1:在上述问题中,若生产一件优质套装获利3万元,生产一件精品套装获利2万元,又当如何安排生产才能获得最大利润?
思考2:在上述问题中,若生产一件优质套装获利1万元,生产一件精品套装获利2万元,又当如何安排生产才能获得最大利润?知识方法思想线性规划的相关概念
解决线性规划问题步骤:建、画、移、求、答.(1)将目标函数值与直线在y轴上的截距相联系;
(2)将目标函数值与点到直线的距离相联系;
(3)代入法;数形结合、转化,从特殊到一般 函数线性规划定义域可行域函数目标函数最值最优化自变量可行解二元函数的最值问题均值不等式线性规划单元小结谢谢各位老师指导
