等比数列的概念(第1课时) 课件(23张PPT)
文档属性
| 名称 | 等比数列的概念(第1课时) 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:33:09 | ||
图片预览








文档简介
课件23张PPT。等比数列第一课时 学习目标:1.知识目标:
1).理解等比数列的定义并证明数列为等比数列;
2).掌握等比数列的通项公式.会解决知道n, 中的三个,求另一个的问题.
2.能力目标:
培养类比思维能力,数学归纳能力及应用数学知识
解决问题的能力。
学习重点:
1.等比数列概念的理解与掌握;
2.等比数列的通项公式的推导及应用.
从第2项起,每一项与它前一项的差等同一个常数
公差(d)d可正可负,且可以为零一:旧知回顾二:创设情景,引入新课有一个巴伊老爷很小气,阿凡提听说后就想治治他。阿凡提给巴伊老爷打工,还说第一天只需支付1分钱,第二天2分,第三天4分,依次类推,每一天都是前一天的2倍,伊巴老爷觉得才几分钱便欣然同意了,大家猜猜看,到第30天,巴伊老爷能支付出工资来吗?(1)1,2,4,8,…观察下列数列,说出它们的特点.定义:如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,记为q(q≠0).数学语言:1.等比数列定义 一般的,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。其数学表达式:(q≠0)1.已知等比数列{ an }:
(1) an 与q能不能是零?
(2)公比q能不能是1?
2.用下列方法表示的数列中能确定
是等比数列的是 .
① 1,-1,1,…,(-1)n+1 ; ②1,2,4,6…;
③a,a,a,…,a; ④已知a1=2,an=3an+1 ;
⑤
⑥2a,2a,2a,…,2a.
3.什么样的数列既是等差数列又是等比数列?不能能√√√×××非零的
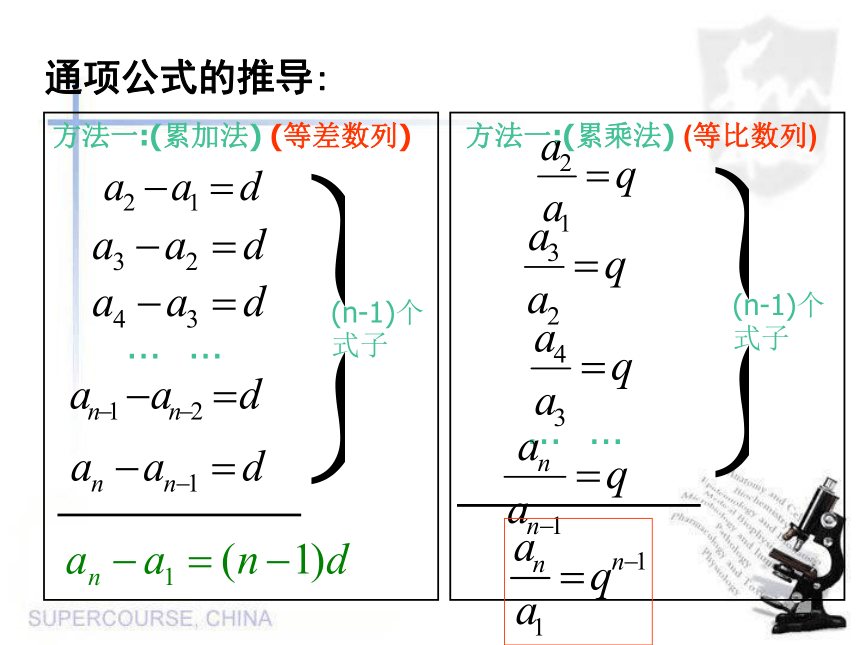
常数列① ④ ⑥思考1:等差数列通项公式的推导:方法一:(累加法)方法一:(累加法) (等差数列)通项公式的推导:方法一:(累乘法) (等比数列)(n-1)个 式子… …通项公式的推导:等比数列通项公式的推导(归纳法)… …2:等比数列的通项公式变形结论:1等比数列通项公式的变形已知等比数列的公比为q,第m项为 ,求 .通项公式通项公式的变形“知三求一”的方程思想 三:应用示例例2:在等比数列{an}中:例3: 一个等比数列的第3项与第4项分别 是12与18,求它的第1项与第2项. 解:设这个等比数列的第1项是 ,公比是q ,
那么 因此a6=a3q3 , 例4:在等比数列{an}中,a3=20 ,q=2 ,求a6 ,an解:a3=a1q2=4a1=20所以 a1=5a6=a1q5=5×32=160a6=8×20=160an=akqn-kan=20×2n-3=5×2n-1四:课堂巩固练习判断-125是否中,练习2.在等比数列为数列中的项,如果是,请指出是第几项. 五.回顾小结从第2项起,每一项与它前一项的比等同一个常数公比q( )
从第2项起,每一项与它前一项的差等同一个常数
公差d可正可负,且可以为零作 业 ⑴ 习题3.4:1,2,3
⑵ 类比等差数列的性质
思考等比数列有何性质
积跬步以致千里,积怠惰以致深渊数学励志公式,用心看,你懂得
1).理解等比数列的定义并证明数列为等比数列;
2).掌握等比数列的通项公式.会解决知道n, 中的三个,求另一个的问题.
2.能力目标:
培养类比思维能力,数学归纳能力及应用数学知识
解决问题的能力。
学习重点:
1.等比数列概念的理解与掌握;
2.等比数列的通项公式的推导及应用.
从第2项起,每一项与它前一项的差等同一个常数
公差(d)d可正可负,且可以为零一:旧知回顾二:创设情景,引入新课有一个巴伊老爷很小气,阿凡提听说后就想治治他。阿凡提给巴伊老爷打工,还说第一天只需支付1分钱,第二天2分,第三天4分,依次类推,每一天都是前一天的2倍,伊巴老爷觉得才几分钱便欣然同意了,大家猜猜看,到第30天,巴伊老爷能支付出工资来吗?(1)1,2,4,8,…观察下列数列,说出它们的特点.定义:如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,记为q(q≠0).数学语言:1.等比数列定义 一般的,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。其数学表达式:(q≠0)1.已知等比数列{ an }:
(1) an 与q能不能是零?
(2)公比q能不能是1?
2.用下列方法表示的数列中能确定
是等比数列的是 .
① 1,-1,1,…,(-1)n+1 ; ②1,2,4,6…;
③a,a,a,…,a; ④已知a1=2,an=3an+1 ;
⑤
⑥2a,2a,2a,…,2a.
3.什么样的数列既是等差数列又是等比数列?不能能√√√×××非零的
常数列① ④ ⑥思考1:等差数列通项公式的推导:方法一:(累加法)方法一:(累加法) (等差数列)通项公式的推导:方法一:(累乘法) (等比数列)(n-1)个 式子… …通项公式的推导:等比数列通项公式的推导(归纳法)… …2:等比数列的通项公式变形结论:1等比数列通项公式的变形已知等比数列的公比为q,第m项为 ,求 .通项公式通项公式的变形“知三求一”的方程思想 三:应用示例例2:在等比数列{an}中:例3: 一个等比数列的第3项与第4项分别 是12与18,求它的第1项与第2项. 解:设这个等比数列的第1项是 ,公比是q ,
那么 因此a6=a3q3 , 例4:在等比数列{an}中,a3=20 ,q=2 ,求a6 ,an解:a3=a1q2=4a1=20所以 a1=5a6=a1q5=5×32=160a6=8×20=160an=akqn-kan=20×2n-3=5×2n-1四:课堂巩固练习判断-125是否中,练习2.在等比数列为数列中的项,如果是,请指出是第几项. 五.回顾小结从第2项起,每一项与它前一项的比等同一个常数公比q( )
从第2项起,每一项与它前一项的差等同一个常数
公差d可正可负,且可以为零作 业 ⑴ 习题3.4:1,2,3
⑵ 类比等差数列的性质
思考等比数列有何性质
积跬步以致千里,积怠惰以致深渊数学励志公式,用心看,你懂得
