第三章 不等式 小结 课件(20张PPT)
文档属性
| 名称 | 第三章 不等式 小结 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:35:57 | ||
图片预览







文档简介
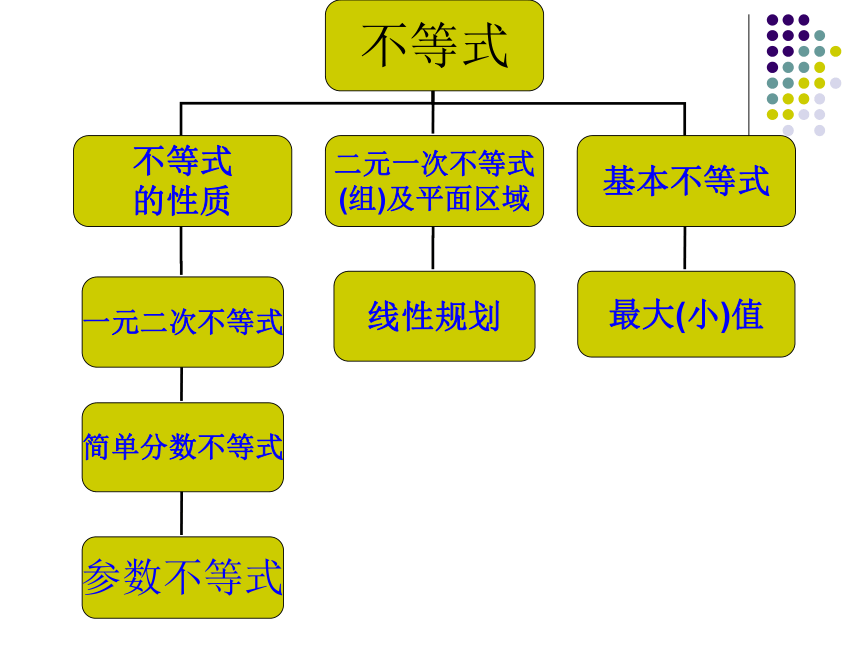
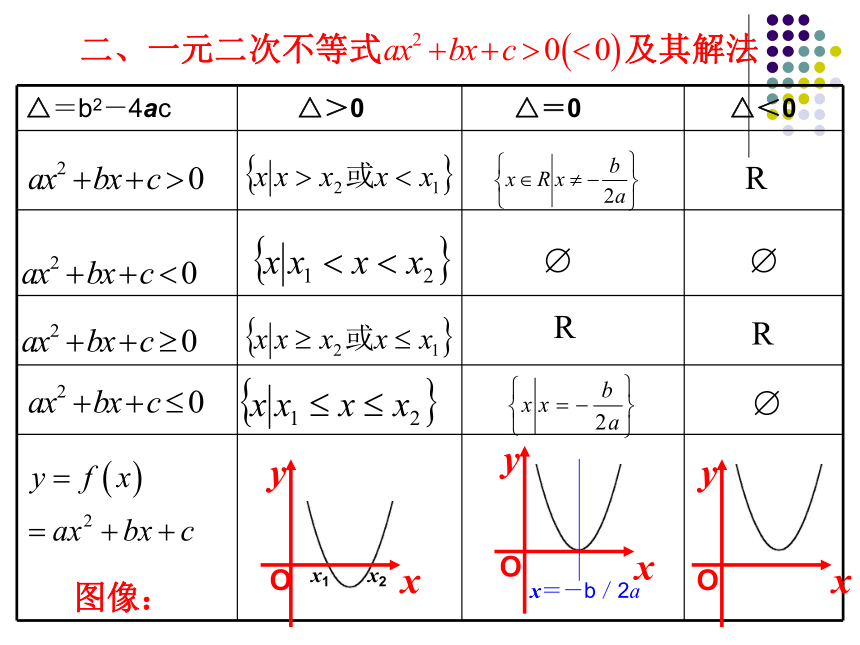
课件20张PPT。必修5第三章第三章复习小结基本知识回顾:一、不等关系与不等式:1、实数 大小比较的基本方法2、不等式的性质:(见下表)?R R ? R?图像:二、一元二次不等式 及其解法三、二元一次不等式(组)与简单的线性规划问题:1、用二元一次不等式(组)表示平面区域的方法:(1)画直线(用实线或虚线表示),(2)带点(常代坐标原点(0,0))确定区域.
2、简单的线性规划问题: 要明确:(1)约束条件; (2)目标函数; (3)可行域; (4)可行解;(5)最优解等概念和判断方法.四、基本不等式:1、重要不等式:2、基本不等式:和定积最大, 积定和最小
题型训练一.不等式的基本性质一、不等式的基本性质1、若a<b<0,则下列不等式中,不能成立的是 ( )
(A)>(B)>(C)|a|>|b|(D)a2>b2则下列不等式中成立的是( )2、已知BB3:解不等式:(1)(2)(3)二.含参一元二次不等式含参数一元二次不等式的解法1.对二次项系数进行大于零,小于零,等于零的分类讨论。
2.当二次项系数不等于零时,再对判别式进行大于零,小于零,等于零的分类讨论。
3.当判别式大于零时,再对两根的大小进行讨论,最后确定出解集。例.解关于x的不等式ax2+(a-2)x-2≥0解: ①a=0时,-2x-2≥0, 解集为 (-∞,-1]
△=(a-2)2+8a=(a+2)2≥0. x1= , x2= -1
②a>0时, >-1 , 解集为
③a<0时
若 <-1即-2若 =-1即a=-2时,-2x2-4x-2≥0,解集为
若 >-1即a<-2时, 解集为 [ -1 , ]三.含参不等式成立问题的解法一、基础知识点:
1、f(x)=ax+b,x [α,β],则:
f(x)>0恒成立< >
f(x)<0恒成立< >2、ax2+bx+c>0在R上恒成立的充要条件是:
______________________。 ax2+bx+c<0在R上恒成立的充要条件是:
______________________。
3、a≥f(x)恒成立的充要条件是:_____________;
a≤f(x)恒成立的充要条件是:_____________。二、典型例题:
例、对于x的不等式 ax2+2bx+1≥0的解集为R,
则a+2b的最小值是( )
A.-2 B.-1 C.0 D.1
四.基本不等式题型
例1:讨论函数 的最值.
利用基本不等式求最值时,各项必须为正数,若为负数,则添负号变正.对于函数
都可用基本不等式求最值.已知x>1,求 x+ 的最小值以及取得最小值时x的值。 解:∵x>1 ∴x-1>0
∴x+ =(x-1)+ +1
≥2 +1=3当且仅当x-1= 即 x=2 时等号成立.
答:最小值是3,取得最小值时x的值为2例2:通过加减项的方法配凑成基本不等式的形式.例3:
已知x>0,y>0 且 ,
求x+y的最小值.例4.函数 的最小
值是___.
2、简单的线性规划问题: 要明确:(1)约束条件; (2)目标函数; (3)可行域; (4)可行解;(5)最优解等概念和判断方法.四、基本不等式:1、重要不等式:2、基本不等式:和定积最大, 积定和最小
题型训练一.不等式的基本性质一、不等式的基本性质1、若a<b<0,则下列不等式中,不能成立的是 ( )
(A)>(B)>(C)|a|>|b|(D)a2>b2则下列不等式中成立的是( )2、已知BB3:解不等式:(1)(2)(3)二.含参一元二次不等式含参数一元二次不等式的解法1.对二次项系数进行大于零,小于零,等于零的分类讨论。
2.当二次项系数不等于零时,再对判别式进行大于零,小于零,等于零的分类讨论。
3.当判别式大于零时,再对两根的大小进行讨论,最后确定出解集。例.解关于x的不等式ax2+(a-2)x-2≥0解: ①a=0时,-2x-2≥0, 解集为 (-∞,-1]
△=(a-2)2+8a=(a+2)2≥0. x1= , x2= -1
②a>0时, >-1 , 解集为
③a<0时
若 <-1即-2
若 >-1即a<-2时, 解集为 [ -1 , ]三.含参不等式成立问题的解法一、基础知识点:
1、f(x)=ax+b,x [α,β],则:
f(x)>0恒成立< >
f(x)<0恒成立< >2、ax2+bx+c>0在R上恒成立的充要条件是:
______________________。 ax2+bx+c<0在R上恒成立的充要条件是:
______________________。
3、a≥f(x)恒成立的充要条件是:_____________;
a≤f(x)恒成立的充要条件是:_____________。二、典型例题:
例、对于x的不等式 ax2+2bx+1≥0的解集为R,
则a+2b的最小值是( )
A.-2 B.-1 C.0 D.1
四.基本不等式题型
例1:讨论函数 的最值.
利用基本不等式求最值时,各项必须为正数,若为负数,则添负号变正.对于函数
都可用基本不等式求最值.已知x>1,求 x+ 的最小值以及取得最小值时x的值。 解:∵x>1 ∴x-1>0
∴x+ =(x-1)+ +1
≥2 +1=3当且仅当x-1= 即 x=2 时等号成立.
答:最小值是3,取得最小值时x的值为2例2:通过加减项的方法配凑成基本不等式的形式.例3:
已知x>0,y>0 且 ,
求x+y的最小值.例4.函数 的最小
值是___.
