1.1.2余弦定理 课件(17张PPT)
文档属性
| 名称 | 1.1.2余弦定理 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 211.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:39:31 | ||
图片预览


文档简介
课件17张PPT。1.1.2 余弦定理
探究新知一、复习回顾
1.正弦定理的内容是什么?
复习回顾练习反馈课堂小结2.正弦定理解决的两类问题是什么?①已知两边及其中一边的对角,求另一边的对角,进而可求其它的边和角。
②已知两角和一边求其它的边和角。二、探究新知
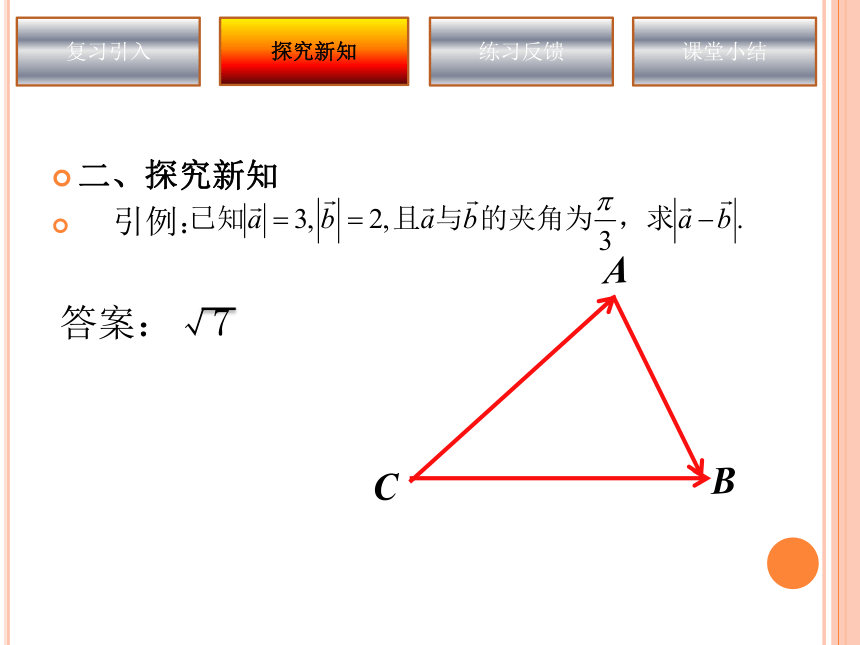
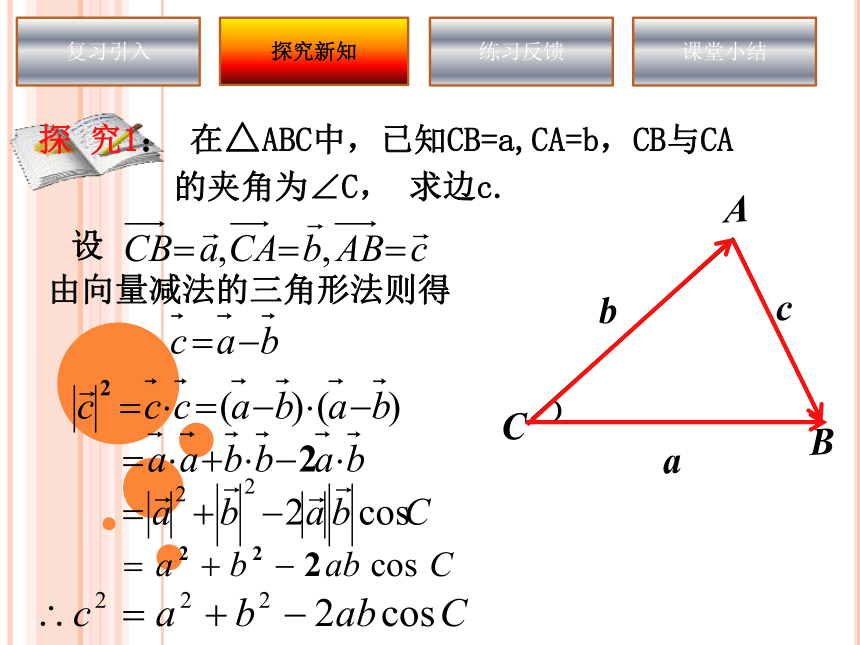
引例:?复习引入探究新知练习反馈课堂小结CBA答案:√7探 究1: 在△ABC中,已知CB=a,CA=b,CB与CA
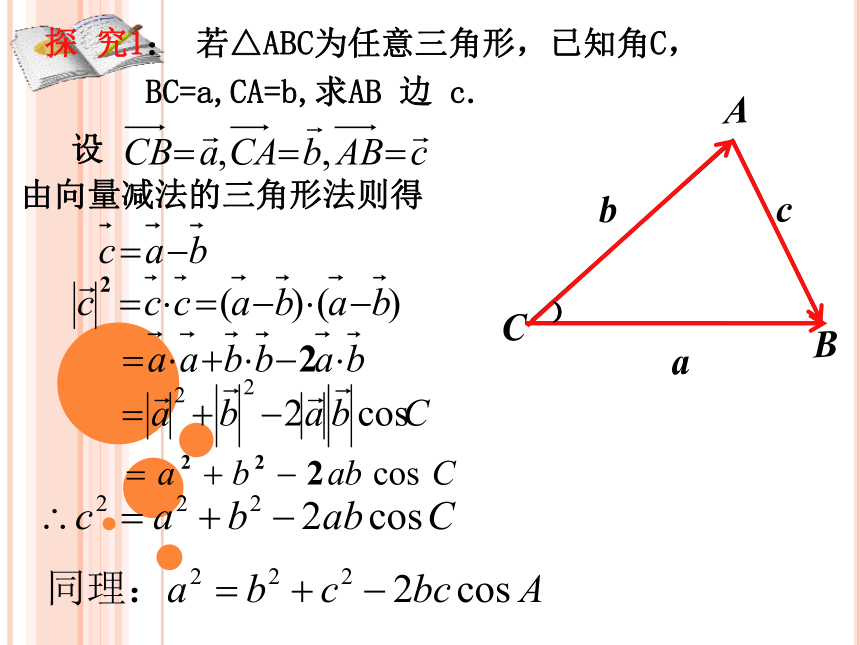
的夹角为∠C, 求边c.﹚由向量减法的三角形法则得复习引入探究新知练习反馈课堂小结CBAcab﹚﹚由向量减法的三角形法则得探 究1: 若△ABC为任意三角形,已知角C,
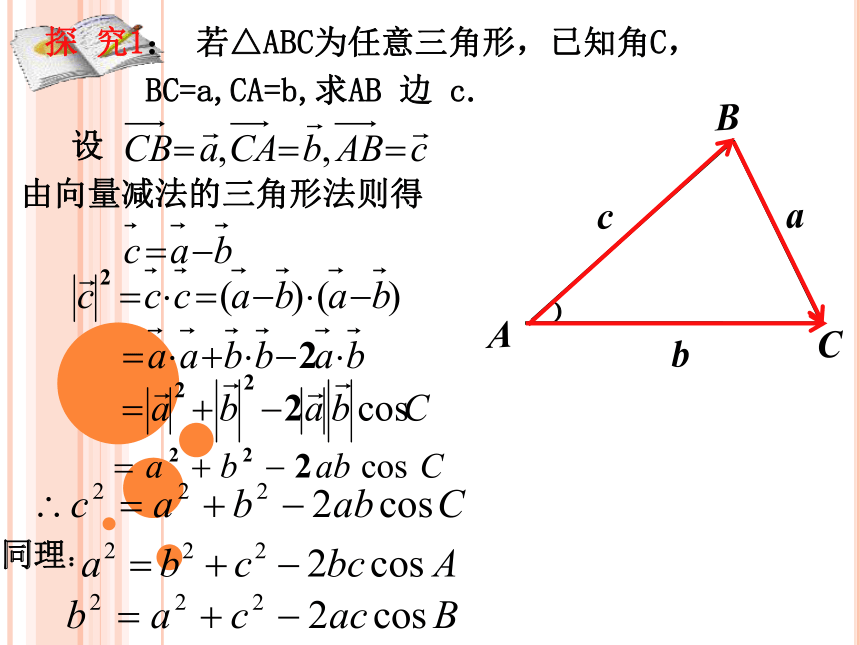
BC=a,CA=b,求AB 边 c.CBAcab﹚由向量减法的三角形法则得探 究1: 若△ABC为任意三角形,已知角C,
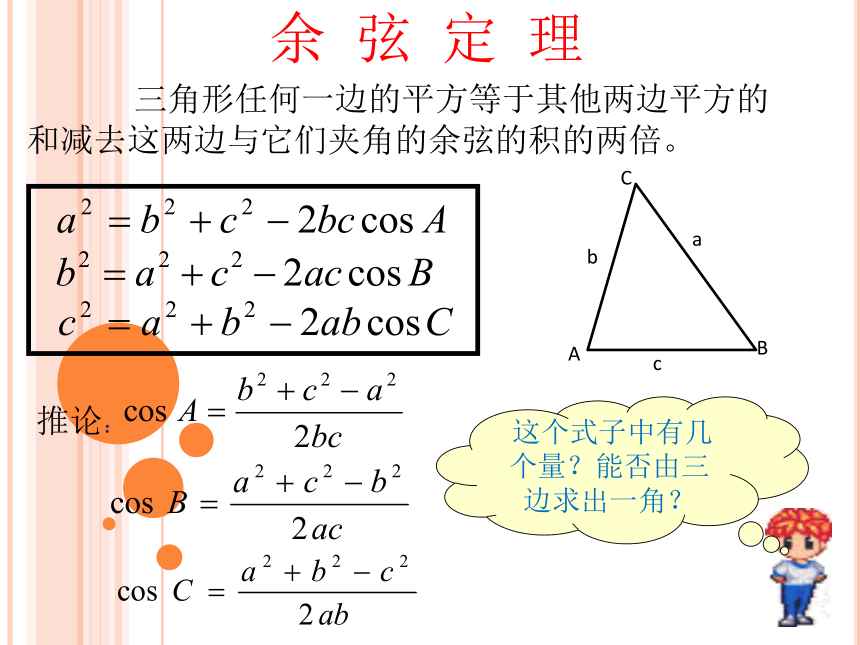
BC=a,CA=b,求AB 边 c.同理:余 弦 定 理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。推论: 这个式子中有几个量?能否由三边求出一角?探 究2A是 角余弦定理及其推论的基本作用:
(1)已知三角形的任意两边及其夹角,就可解三角形;
拓展:已知三角形任意两边及一角就可解三角形。
(2)已知三角形三边求其它角。复习引入探究新知练习反馈拓展提高A是 角A是 角问题:如何才能判断锐角三角形?锐钝直练一练:在△ABC中,已知 a=7,b=5 ,c=3 ,判断△ABC的类型。答案:钝角三角形复习引入探究新知练习反馈课堂小结复习引入练习反馈探究新知课堂小结变式探究1:本例中,条件不变,求角B、C。
复习引入练习反馈探究新知课堂小结解法一:利用余弦定理将角化为边.
∵bcosA=acosB,∴b2+c2-a2=a2+c2-b2.∴a2=b2.
∴a=b.故此三角形是等腰三角形.
解法二:利用正弦定理将边转化为角.
∵bcosA=acosB,b=2RsinB,a=2RsinA,
∴2RsinBcosA=2RsinAcosB.
∴sinAcosB-cosAsinB=0.∴sin(A-B)=0.
∵0<A,B<π,∴-π<A-B<π.
∴A-B=0,即A=B.故此三角形是等腰三角形.复习引入练习反馈探究新知课堂小结解法1:由条件知:复习引入练习反馈探究新知拓展提高解法2:由条件知:四、课堂小结1、余弦定理及其推论的表达形式
2、余弦定理可以解决的有关三角形的问题:(1)已知三角形的任意两边及其夹角,就可解三角形;
拓展:已知三角形任意两边及一角就可解三角形。
(2)已知三角形三边解三角形。
(3)判断三角形的形状。复习引入课堂小结探究新知练习反馈五、课后作业(1)《导与练》56页。
(2) 课后拓展:1. 在△ABC中,已知(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,试确定△ABC的形状。
2. (2014新课标II卷) 四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(Ⅰ)求 角C和BD ;
(Ⅱ)求四边形 ABCD的面积.
谢 谢 指 导
1.正弦定理的内容是什么?
复习回顾练习反馈课堂小结2.正弦定理解决的两类问题是什么?①已知两边及其中一边的对角,求另一边的对角,进而可求其它的边和角。
②已知两角和一边求其它的边和角。二、探究新知
引例:?复习引入探究新知练习反馈课堂小结CBA答案:√7探 究1: 在△ABC中,已知CB=a,CA=b,CB与CA
的夹角为∠C, 求边c.﹚由向量减法的三角形法则得复习引入探究新知练习反馈课堂小结CBAcab﹚﹚由向量减法的三角形法则得探 究1: 若△ABC为任意三角形,已知角C,
BC=a,CA=b,求AB 边 c.CBAcab﹚由向量减法的三角形法则得探 究1: 若△ABC为任意三角形,已知角C,
BC=a,CA=b,求AB 边 c.同理:余 弦 定 理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。推论: 这个式子中有几个量?能否由三边求出一角?探 究2A是 角余弦定理及其推论的基本作用:
(1)已知三角形的任意两边及其夹角,就可解三角形;
拓展:已知三角形任意两边及一角就可解三角形。
(2)已知三角形三边求其它角。复习引入探究新知练习反馈拓展提高A是 角A是 角问题:如何才能判断锐角三角形?锐钝直练一练:在△ABC中,已知 a=7,b=5 ,c=3 ,判断△ABC的类型。答案:钝角三角形复习引入探究新知练习反馈课堂小结复习引入练习反馈探究新知课堂小结变式探究1:本例中,条件不变,求角B、C。
复习引入练习反馈探究新知课堂小结解法一:利用余弦定理将角化为边.
∵bcosA=acosB,∴b2+c2-a2=a2+c2-b2.∴a2=b2.
∴a=b.故此三角形是等腰三角形.
解法二:利用正弦定理将边转化为角.
∵bcosA=acosB,b=2RsinB,a=2RsinA,
∴2RsinBcosA=2RsinAcosB.
∴sinAcosB-cosAsinB=0.∴sin(A-B)=0.
∵0<A,B<π,∴-π<A-B<π.
∴A-B=0,即A=B.故此三角形是等腰三角形.复习引入练习反馈探究新知课堂小结解法1:由条件知:复习引入练习反馈探究新知拓展提高解法2:由条件知:四、课堂小结1、余弦定理及其推论的表达形式
2、余弦定理可以解决的有关三角形的问题:(1)已知三角形的任意两边及其夹角,就可解三角形;
拓展:已知三角形任意两边及一角就可解三角形。
(2)已知三角形三边解三角形。
(3)判断三角形的形状。复习引入课堂小结探究新知练习反馈五、课后作业(1)《导与练》56页。
(2) 课后拓展:1. 在△ABC中,已知(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,试确定△ABC的形状。
2. (2014新课标II卷) 四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(Ⅰ)求 角C和BD ;
(Ⅱ)求四边形 ABCD的面积.
谢 谢 指 导
