1.1.2余弦定理 课件(18张PPT)
文档属性
| 名称 | 1.1.2余弦定理 课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:40:56 | ||
图片预览





文档简介
课件18张PPT。1.1 正弦定理和余弦定理1.1.2 余弦定理 本节课主要学习余弦定理及推导过程、用余弦定理解三角形、判断三角形形状。以苏格拉底几何原本由来的故事和高铁隧道招标的事例作为本节的开始引入新课。本节教学以学生探究为主,利用向量法证明余弦定理定理,引导学生探究坐标法、直角三角形边角关系法、正弦定理法等多种方法证明余弦定理,使学生能够灵活应用所学知识,加深对定理的理解。针对定理所解决的三类问题给出3个例题和变式,通过解决问题引出三角形的解的不同情况,强调正确应用定理的重要性。
教学过程中通过例1巩固掌握已知两边及其夹角解三角形的问题,通过例2巩固掌握已知三边解三角形的问题,通过例3巩固掌握判断三角形形状的问题,每种类型都有变式进行巩固。用直角三角形的边角关系证明余弦定理导,既节省时间又能吸引学生注意力。通过余弦定理的推导和用余弦定理解决问题两个探究指明本节课的方向。由探究二余弦定理可以解决的问题引出余弦定理的变形及用余弦定理判断三角形的形状等知识。
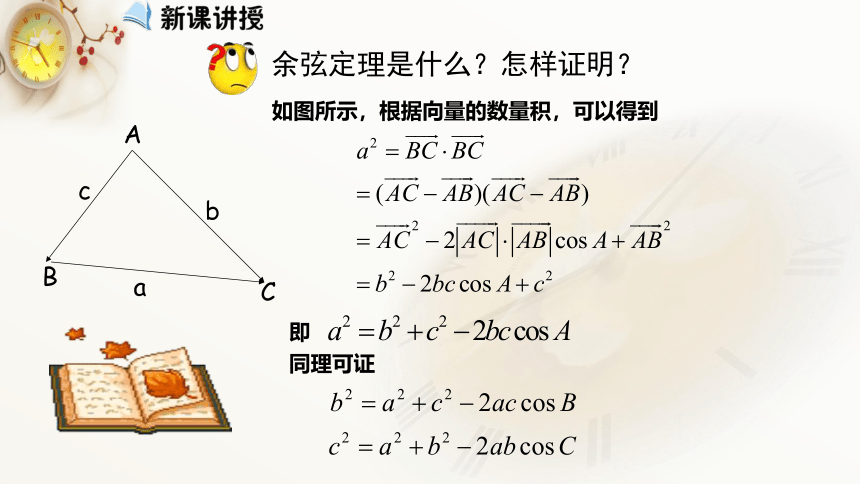
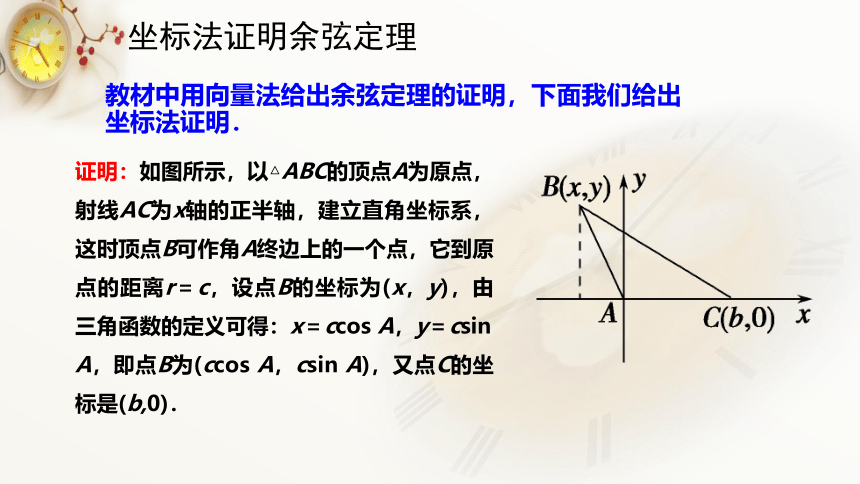
即同理可证如图所示,根据向量的数量积,可以得到cabBAC余弦定理是什么?怎样证明? 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。余弦定理: 回顾正弦定理的证明你还有没有其它的证明余弦定理的方法?(1)坐标法(2)直角三角形的边角关系(3)正弦定理(三角变换) 证 明 方 法证明:如图所示,以△ABC的顶点A为原点,射线AC为x轴的正半轴,建立直角坐标系,这时顶点B可作角A终边上的一个点,它到原点的距离r=c,设点B的坐标为(x,y),由三角函数的定义可得:x=ccos A,y=csin A,即点B为(ccos A,csin A),又点C的坐标是(b,0).坐标法证明余弦定理教材中用向量法给出余弦定理的证明,下面我们给出坐标法证明.思考:你会用直角三角形或正弦定理来证明余弦定理吗? 想一想: 余弦定理能够解决什么问题? a2=b2+c2-2bccosA
b2=c2+a2-2cacosB
c2=a2+b2-2abcosC方程思想:四个量,知三求一
1.已知两边和它们的夹角求另一边(直接用);
2.已知三边求角(变形).
3.判断三角形形状
例1.回到引例. 如图,在△ABC中,已知a=5,b=4,∠C=120°,求c.解:由余弦定理,得因此已知在ΔABC中,根据下列条件解三角形。变式训练一:?已知在ΔABC中,根据下列条件解三角形。例2.已知,在△ABC三边长为:a=5,b=4,c= ,求三角形的最大内角。已知在ΔABC中,根据下列条件解三角形。变式训练二:解:?????????.例3.已知在△ABC中,
试判断该三角形的形状 变式训练三:.已知在△ABC中,
则三角形为( )
A 直角三角形 B 锐角三角形
C 等腰三角形 D等边三角形三角形中的边角关系余弦定理定理内容定理证明定理应用(1)已知三边,求三个角(2)已知两边和它们的夹角,
求第三边和其它两个角。(3)判断三角形形状1、课本1页:习题1.1
A组:第3题
2、练习册:金版案
教学过程中通过例1巩固掌握已知两边及其夹角解三角形的问题,通过例2巩固掌握已知三边解三角形的问题,通过例3巩固掌握判断三角形形状的问题,每种类型都有变式进行巩固。用直角三角形的边角关系证明余弦定理导,既节省时间又能吸引学生注意力。通过余弦定理的推导和用余弦定理解决问题两个探究指明本节课的方向。由探究二余弦定理可以解决的问题引出余弦定理的变形及用余弦定理判断三角形的形状等知识。
即同理可证如图所示,根据向量的数量积,可以得到cabBAC余弦定理是什么?怎样证明? 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。余弦定理: 回顾正弦定理的证明你还有没有其它的证明余弦定理的方法?(1)坐标法(2)直角三角形的边角关系(3)正弦定理(三角变换) 证 明 方 法证明:如图所示,以△ABC的顶点A为原点,射线AC为x轴的正半轴,建立直角坐标系,这时顶点B可作角A终边上的一个点,它到原点的距离r=c,设点B的坐标为(x,y),由三角函数的定义可得:x=ccos A,y=csin A,即点B为(ccos A,csin A),又点C的坐标是(b,0).坐标法证明余弦定理教材中用向量法给出余弦定理的证明,下面我们给出坐标法证明.思考:你会用直角三角形或正弦定理来证明余弦定理吗? 想一想: 余弦定理能够解决什么问题? a2=b2+c2-2bccosA
b2=c2+a2-2cacosB
c2=a2+b2-2abcosC方程思想:四个量,知三求一
1.已知两边和它们的夹角求另一边(直接用);
2.已知三边求角(变形).
3.判断三角形形状
例1.回到引例. 如图,在△ABC中,已知a=5,b=4,∠C=120°,求c.解:由余弦定理,得因此已知在ΔABC中,根据下列条件解三角形。变式训练一:?已知在ΔABC中,根据下列条件解三角形。例2.已知,在△ABC三边长为:a=5,b=4,c= ,求三角形的最大内角。已知在ΔABC中,根据下列条件解三角形。变式训练二:解:?????????.例3.已知在△ABC中,
试判断该三角形的形状 变式训练三:.已知在△ABC中,
则三角形为( )
A 直角三角形 B 锐角三角形
C 等腰三角形 D等边三角形三角形中的边角关系余弦定理定理内容定理证明定理应用(1)已知三边,求三个角(2)已知两边和它们的夹角,
求第三边和其它两个角。(3)判断三角形形状1、课本1页:习题1.1
A组:第3题
2、练习册:金版案
