3.3 线性规划 课件(20张PPT)
文档属性
| 名称 | 3.3 线性规划 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 260.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:43:02 | ||
图片预览






文档简介
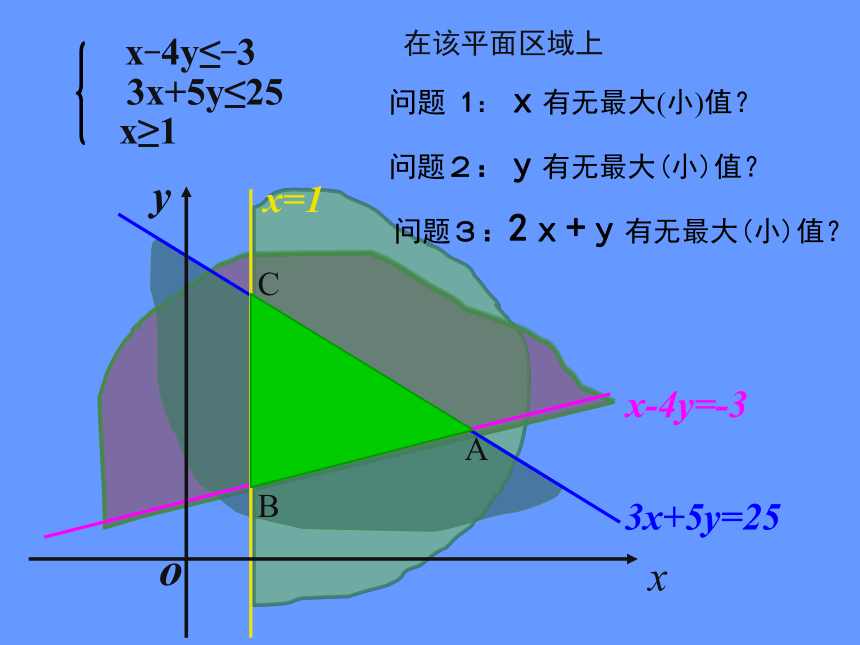
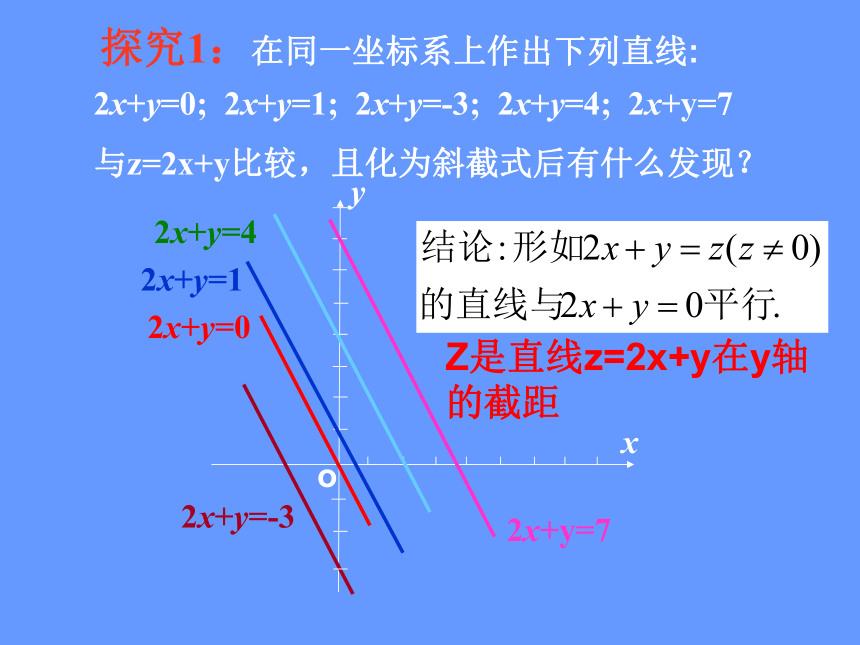
课件20张PPT。简单线性规划问题2. 包括边界的区域将边界画成实线,不包括边界的区域将边界画成虚线.1.画二元一次不等式表示的平面区域,常采用“直线定界,特殊点定域”的方法,当边界不过原点时,常把原点作为特殊点.3. 不等式Ax+By+C>0表示的平面区域位置与A、B的符号有关(同为正,异为负),相关理论不要求掌握.画出不等式组 表示的平面区域。3x+5y≤ 25 x -4y≤ - 3x≥1引例3x+5y≤25x-4y≤-3x≥1问题2:y有无最大(小)值?xyo问题3:2x+y有无最大(小)值?二.提出问题把上面的问题综合起来:设z=2x+y,求满足时,求z的最大值和最小值.探究1:在同一坐标系上作出下列直线:2x+y=0; 2x+y=1; 2x+y=-3; 2x+y=4; 2x+y=7
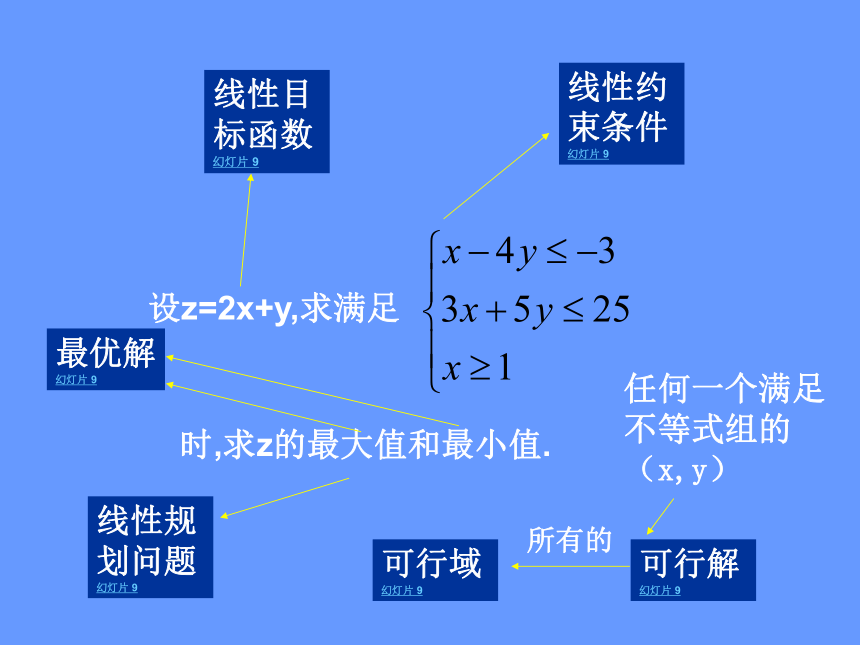
与z=2x+y比较,且化为斜截式后有什么发现?xyo2x+y=0 2x+y=12x+y=42x+y=72x+y=-3Z是直线z=2x+y在y轴的截距ABCA直线 l 越往右平移,t随之增大.以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.线性目标函数幻灯片 9线性约束条件幻灯片 9线性规划问题幻灯片 9任何一个满足不等式组的(x,y)可行解幻灯片 9可行域幻灯片 9所有的最优解幻灯片 9最优解:使目标函数达到最大值或 最小值 的可 行 解。 线性约束条件:约束条件中均为关于x、y的一次不等式或方程。有关概念 约束条件:由x、y的不等式(方程)构成的不等式组。目标函数:欲求最值的关于x、y的解析式。线性目标函数:欲求最值的解析式是关于x、y的一次解析式。线性规划:求线性目标函数在线性约束条件下的最大值或最小值。可行解:满足线性约束条件的解(x,y)。 可行域:所有可行解组成的集合。探究2:目标函数z的几何意义
若目标函数为z=Ax+By(B不为0),且把目标函数化为斜截式的形式,探究目标函数z的几何意义
Z是直线在y轴上截距的B倍
当B>0时,截距越大,z越大;
当B<0时,截距越小,z越大线性规划的图解法12解线性规划问题的步骤: 1.画:画出线性约束条件所表示的可行域; 2.移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点
且纵截距最大或最小的直线; 3.求:通过解方程组求出最优解; 4.答:作出答案。 ,求z的最大值和最小值.理论迁移5,求z的最大值和最小值.2x-y=0代入点B得最大为8,代入点A得
最小值为 .3X+5y ≤25A(1,4.4)
B(5,,2)
C(1,1) 分析:令目标函数z为0,
作直线平移,使之与可行域有交点。 最小截距为过A(5,2)
的直线注意:此题y的系数为负,当直线取最大截距时,代入点C,则z有最小值同理,当直线取最小截距时,代入点A,则z有最大值 最大截距为过
的直线变题:上例若改为求z=x-2y的最大值、最小值呢?探究3:最优解与可行域的关系通过上述习题探究最优解与可行域之间的关系?
1) 线性目标函数的最值一般在可行域的顶点或边界处取得,在哪个顶点不仅与B有关,还与目标函数的斜率有关,其斜率与可行域边界所在直线斜率的大小关系一定要弄清楚.
2) 线性目标函数的最优解个数可能有一个或多个或无数个归纳小结1. 1.线性约束条件、线性目标函数、可行域、可行解等基本概念的理解;.2.线性目标函数的最值的图解法及其步骤.
错在哪儿?怎么做呢?作业课本p91 练习
谢谢!
与z=2x+y比较,且化为斜截式后有什么发现?xyo2x+y=0 2x+y=12x+y=42x+y=72x+y=-3Z是直线z=2x+y在y轴的截距ABCA直线 l 越往右平移,t随之增大.以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.线性目标函数幻灯片 9线性约束条件幻灯片 9线性规划问题幻灯片 9任何一个满足不等式组的(x,y)可行解幻灯片 9可行域幻灯片 9所有的最优解幻灯片 9最优解:使目标函数达到最大值或 最小值 的可 行 解。 线性约束条件:约束条件中均为关于x、y的一次不等式或方程。有关概念 约束条件:由x、y的不等式(方程)构成的不等式组。目标函数:欲求最值的关于x、y的解析式。线性目标函数:欲求最值的解析式是关于x、y的一次解析式。线性规划:求线性目标函数在线性约束条件下的最大值或最小值。可行解:满足线性约束条件的解(x,y)。 可行域:所有可行解组成的集合。探究2:目标函数z的几何意义
若目标函数为z=Ax+By(B不为0),且把目标函数化为斜截式的形式,探究目标函数z的几何意义
Z是直线在y轴上截距的B倍
当B>0时,截距越大,z越大;
当B<0时,截距越小,z越大线性规划的图解法12解线性规划问题的步骤: 1.画:画出线性约束条件所表示的可行域; 2.移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点
且纵截距最大或最小的直线; 3.求:通过解方程组求出最优解; 4.答:作出答案。 ,求z的最大值和最小值.理论迁移5,求z的最大值和最小值.2x-y=0代入点B得最大为8,代入点A得
最小值为 .3X+5y ≤25A(1,4.4)
B(5,,2)
C(1,1) 分析:令目标函数z为0,
作直线平移,使之与可行域有交点。 最小截距为过A(5,2)
的直线注意:此题y的系数为负,当直线取最大截距时,代入点C,则z有最小值同理,当直线取最小截距时,代入点A,则z有最大值 最大截距为过
的直线变题:上例若改为求z=x-2y的最大值、最小值呢?探究3:最优解与可行域的关系通过上述习题探究最优解与可行域之间的关系?
1) 线性目标函数的最值一般在可行域的顶点或边界处取得,在哪个顶点不仅与B有关,还与目标函数的斜率有关,其斜率与可行域边界所在直线斜率的大小关系一定要弄清楚.
2) 线性目标函数的最优解个数可能有一个或多个或无数个归纳小结1. 1.线性约束条件、线性目标函数、可行域、可行解等基本概念的理解;.2.线性目标函数的最值的图解法及其步骤.
错在哪儿?怎么做呢?作业课本p91 练习
谢谢!
