3.4 基本不等式小结 课件(27张PPT)
文档属性
| 名称 | 3.4 基本不等式小结 课件(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 489.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:48:26 | ||
图片预览







文档简介
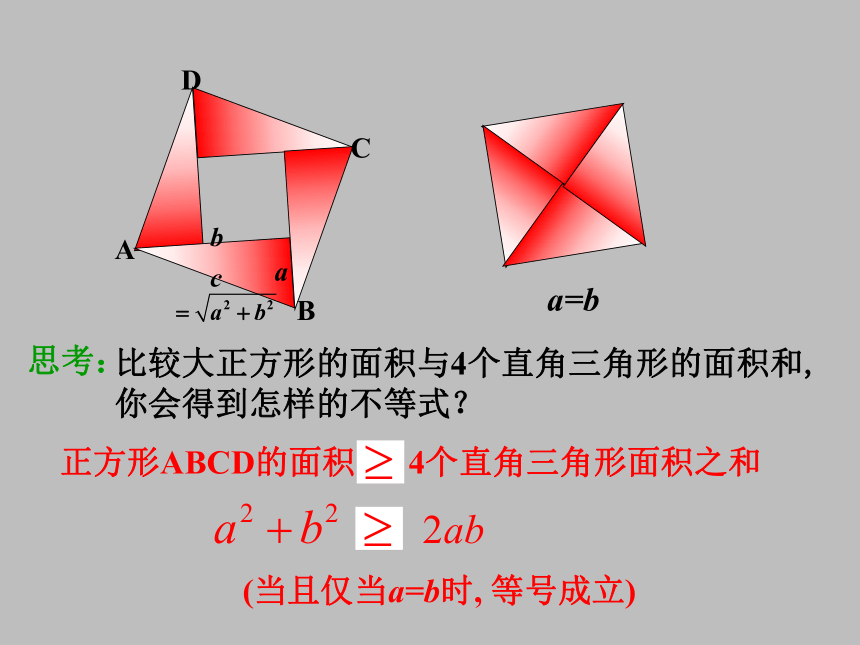
课件27张PPT。§3.4 基本不等式小结 左图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。你能在这个图中找出一些相等关系或不等关系吗?(当且仅当a=b时, 等号成立)正方形ABCD的面积 > 4个直角三角形面积之和a=bADCB 推广: 思考:你能给出它的证明吗? 证明:因为 所以 即一般地,对于任意实数 ,我们有
当且仅当 时,等号成立。当 时, 当 时,一般地,我们把不等式重要不等式 思考:如果用 去替换 中的 ,
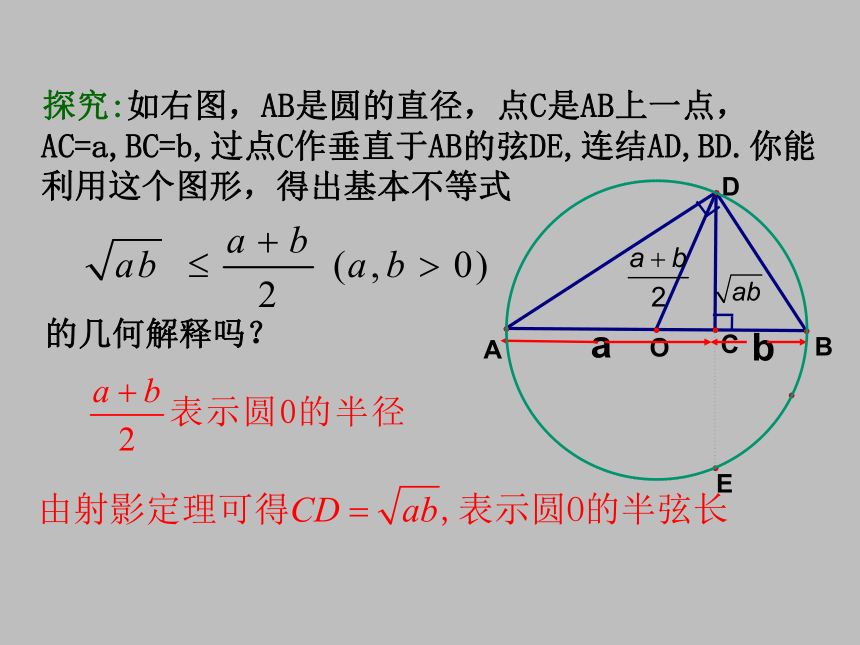
能得到什么结论? 必须要满足什么条件?基本不等式证明: 探究:如右图,AB是圆的直径,点C是AB上一点,AC=a,BC=b,过点C作垂直于AB的弦DE,连结AD,BD.你能利用这个图形,得出基本不等式
的几何解释吗?2.几何意义:半弦长小于等于半径(当且仅当a=b时,等号成立) 探究:基本不等式
的几何解释3.代数意义:几何平均数小于等于算术平均数 注意:基本不等式
的几个变形式:(当且仅当a=b时,等号成立)例1:(1)用篱笆围成一个面积为100m2的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短。
最短的篱笆是多少?解:设矩形菜园的长为x m,宽为y m, 则xy=100,篱笆的长为2(x+y)m. 等号当且仅当x=y时成立,此时x=y=10. 因此,这个矩形的长、宽都为10m时,所用的篱笆最短最短的篱笆是40m. 结论1.两个正数积为定值,则和有最小值三、例题例1:(2)用一段长为36m的篱笆围成一个矩形菜园,
问这个矩形菜园的长和宽各为多少时,菜园的面
积最大,最大面积是多少?三、例题解:设矩形菜园的长为x m,宽为y m, 则 2(x + y)= 36 , x+ y =18矩形菜园的面积为xy m2得 xy ≤ 81当且仅当x=y,即x=y=9时,等号成立 因此,这个矩形的长、宽都为9m时,
菜园面积最大,最大面积是81m2结论2.两个正数和为定值,则积有最大值小大例2、若 ,求 的最小值.发现运算结构,应用不等式变1:若 求 的最小值变2:若 ,求 的最小值.例3、若 ,求 的最大值.×构造定值条件例4:若 ,求 的最小值.×构造定值条件变3×例5:若 求 有无最值?变4:若 求 有无最值?变5×算术平均数几何平均数课后作业
活页 3.4.1
当且仅当 时,等号成立。当 时, 当 时,一般地,我们把不等式重要不等式 思考:如果用 去替换 中的 ,
能得到什么结论? 必须要满足什么条件?基本不等式证明: 探究:如右图,AB是圆的直径,点C是AB上一点,AC=a,BC=b,过点C作垂直于AB的弦DE,连结AD,BD.你能利用这个图形,得出基本不等式
的几何解释吗?2.几何意义:半弦长小于等于半径(当且仅当a=b时,等号成立) 探究:基本不等式
的几何解释3.代数意义:几何平均数小于等于算术平均数 注意:基本不等式
的几个变形式:(当且仅当a=b时,等号成立)例1:(1)用篱笆围成一个面积为100m2的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短。
最短的篱笆是多少?解:设矩形菜园的长为x m,宽为y m, 则xy=100,篱笆的长为2(x+y)m. 等号当且仅当x=y时成立,此时x=y=10. 因此,这个矩形的长、宽都为10m时,所用的篱笆最短最短的篱笆是40m. 结论1.两个正数积为定值,则和有最小值三、例题例1:(2)用一段长为36m的篱笆围成一个矩形菜园,
问这个矩形菜园的长和宽各为多少时,菜园的面
积最大,最大面积是多少?三、例题解:设矩形菜园的长为x m,宽为y m, 则 2(x + y)= 36 , x+ y =18矩形菜园的面积为xy m2得 xy ≤ 81当且仅当x=y,即x=y=9时,等号成立 因此,这个矩形的长、宽都为9m时,
菜园面积最大,最大面积是81m2结论2.两个正数和为定值,则积有最大值小大例2、若 ,求 的最小值.发现运算结构,应用不等式变1:若 求 的最小值变2:若 ,求 的最小值.例3、若 ,求 的最大值.×构造定值条件例4:若 ,求 的最小值.×构造定值条件变3×例5:若 求 有无最值?变4:若 求 有无最值?变5×算术平均数几何平均数课后作业
活页 3.4.1
