简单的线性规划小结 课件(24张PPT)
文档属性
| 名称 | 简单的线性规划小结 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 210.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 12:45:38 | ||
图片预览








文档简介
课件24张PPT。简单的线性规划从近几年的高考题看,无论是课标卷,全国卷还是其它省市的试卷,几乎每年都会出现一个,也就是说本节课的内容是高考的必考内容,考查的形式基本上是填空或选择,希望同学们重视起来!?教学目标
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;?
2.运用线性规划问题的图解法,解决一些简单的实际问题.??
教学重点与难点:
重点是掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;?运用线性规划问题的图解法,并能应用它解决一些简单的实际问题.
难点是把实际问题转化为线性规划问题,并给出解答.解决难点的关键是根据约束条件和目标函数,利用图解法求得最优解.为突出重点,本节教学应指导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化.
复习回顾:画一元二次不等式(组)表示的平面区域采用的方法。?
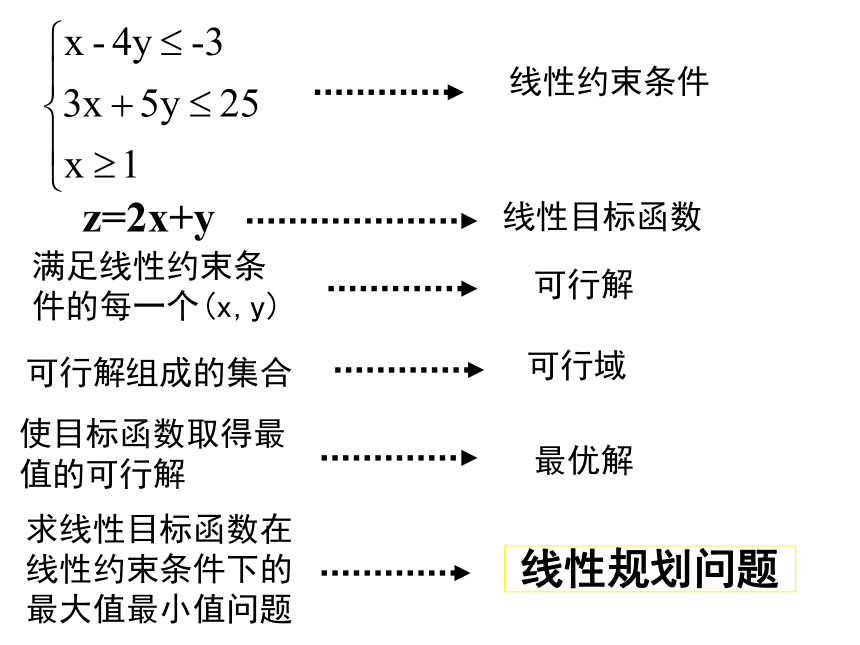
直线定界,特殊点定域特殊地,C不为 0时,常把原点作为此特殊点。线性约束条件z=2x+y线性目标函数可行域可行解组成的集合满足线性约束条件的每一个(x,y)可行解使目标函数取得最 值的可行解最优解求线性目标函数在线性约束条件下的最大值最小值问题线性规划问题解线性规划题目的一般步骤:1、画:画出线性约束条件所表示的可行域;2、移:在线性目标函数所表示的一组平行线中,利用平移找出与可行域有公共点且纵截距最大或最小的直线;3、求:通过解方程组求出最优解;4、答:做出答案。1)求z=2x-y的最值例2:2)求z=x+2y的最值 例2 :3)求z=3x+5y的最值 例2 :例2 :P例2 :P6)若 z=ax+y取得最大值的最优解有无数个, 求实数a的值例2 :7)若 z=ax+y取得最小值的最优解有无数个, 求实数a的值例2 :练习一:练习一:练习一:练习一:练习二:B(4,0) 2、三角形三边所在直线方程分别是
x-y+5=0,x+y=0,x-3=0,
用不等式组表示三角形的内部区域(包含边界).4.在如图所示的坐标平面的可行域内(阴影部分且包括周界),目标函数z=x+ay取得最小值的最优解有无数个,则a的一个可能值为( )
(A)-3 (B)3 (C)-1 (D)1A5.在如图所示的坐标平面的可行域内(阴影部分且包括周界),目标函数z=x+ay取得最大值的最优解有无数个,则a的一个可能值为( )
(A)-3 (B)3 (C)-1 (D)1D1、线性规划问题的有关概念小结:2、线性规划问题的解题步骤
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;?
2.运用线性规划问题的图解法,解决一些简单的实际问题.??
教学重点与难点:
重点是掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;?运用线性规划问题的图解法,并能应用它解决一些简单的实际问题.
难点是把实际问题转化为线性规划问题,并给出解答.解决难点的关键是根据约束条件和目标函数,利用图解法求得最优解.为突出重点,本节教学应指导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化.
复习回顾:画一元二次不等式(组)表示的平面区域采用的方法。?
直线定界,特殊点定域特殊地,C不为 0时,常把原点作为此特殊点。线性约束条件z=2x+y线性目标函数可行域可行解组成的集合满足线性约束条件的每一个(x,y)可行解使目标函数取得最 值的可行解最优解求线性目标函数在线性约束条件下的最大值最小值问题线性规划问题解线性规划题目的一般步骤:1、画:画出线性约束条件所表示的可行域;2、移:在线性目标函数所表示的一组平行线中,利用平移找出与可行域有公共点且纵截距最大或最小的直线;3、求:通过解方程组求出最优解;4、答:做出答案。1)求z=2x-y的最值例2:2)求z=x+2y的最值 例2 :3)求z=3x+5y的最值 例2 :例2 :P例2 :P6)若 z=ax+y取得最大值的最优解有无数个, 求实数a的值例2 :7)若 z=ax+y取得最小值的最优解有无数个, 求实数a的值例2 :练习一:练习一:练习一:练习一:练习二:B(4,0) 2、三角形三边所在直线方程分别是
x-y+5=0,x+y=0,x-3=0,
用不等式组表示三角形的内部区域(包含边界).4.在如图所示的坐标平面的可行域内(阴影部分且包括周界),目标函数z=x+ay取得最小值的最优解有无数个,则a的一个可能值为( )
(A)-3 (B)3 (C)-1 (D)1A5.在如图所示的坐标平面的可行域内(阴影部分且包括周界),目标函数z=x+ay取得最大值的最优解有无数个,则a的一个可能值为( )
(A)-3 (B)3 (C)-1 (D)1D1、线性规划问题的有关概念小结:2、线性规划问题的解题步骤
