华师大版七年级上册 第4章 图形的初步认识 单元测试(含答案)
文档属性
| 名称 | 华师大版七年级上册 第4章 图形的初步认识 单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 161.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 12:03:31 | ||
图片预览



文档简介
第4章图形的初步认识 水平测试
一、选择题(每小题3分,共30分)
1.修建高速公路时,经常将弯曲的道路改直,从而缩短路程,这样做的数学根据是( )
A.两点确定一条直线 B.两点之间,线段最短
C.垂线段最短 D.同位角相等,两直线平行
2.下列说法正确的是( )
①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.
A.①② B.①③ C.②③ D.①②③
3.如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )
A.敬 B.业 C.诚 D.信
4.如图,点B、C、D依次在射线AP上,根据图示,下列线段长度错误的是( )
A.AD=2a B.BC=a﹣b C.BD=a﹣b D.AC=2a﹣b
5.如图所示为某几何体的示意图,该几何体的左视图应为( )
A. B. C. D.
6.已知∠α的补角为125°12′,则它的余角为( )
A.35°12′ B.35°48′ C.55°12′ D.55°48′
7.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有( )
A.1个 B.2个 C.3个 D.4个
8.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )
A.50° B.65° C.75° D.60°
9.如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
A.4 B.6 C.8 D.10
10.一个几何体由一些小正方体摆成,其主视图与左视图如图所示,其俯视图不可能( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.如图所示,按要求填写.其中多面体有: .
12.一个几何体的表面展开图如图所示,则这个几何体是 .
13.一个多边形有8条边,从其中的一个顶点出发,连接这个点和其他顶点,
可以得到 个三角形.
14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 .
15.如图,一长方体木板上有两个洞,一个是正方形形状的,一个是圆形形状的,对于以下4种几何体,你觉得哪一种作为塞子既可以堵住圆形空洞又可以堵住方形空洞? (填序号).
16.如图所示,∠AOB是平角,∠COD=90°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于 度.
17.已知A、B、C三点在同一直线上,线段AB=10,BC=4,则线段AC= .
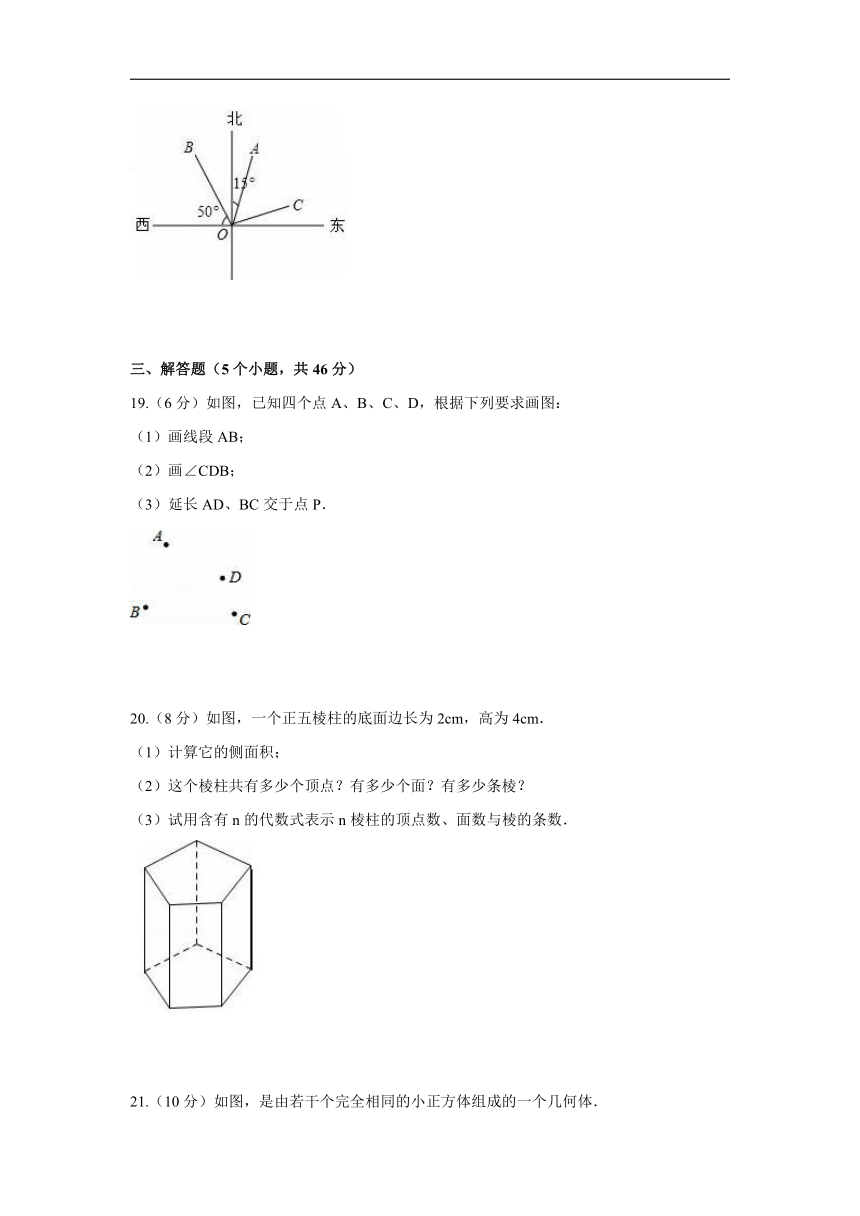
18.如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是 .
三、解答题(5个小题,共46分)
19.(6分)如图,已知四个点A、B、C、D,根据下列要求画图:
(1)画线段AB;
(2)画∠CDB;
(3)延长AD、BC交于点P.
20.(8分)如图,一个正五棱柱的底面边长为2cm,高为4cm.
(1)计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少个面?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.
21.(10分)如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
22.(10分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°,求∠COD的度数.
23.(12分)如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=acm,其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣CB=bcm,M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
附加题:(每小题10分,共20分)
24.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
25.已知∠AOB=160°,∠COE=80°,OF平分∠AOE.
(1)如图1,若∠COF=14°,则∠BOE= ;若∠COF=n°,则∠BOE= ,∠BOE与∠COF的数量关系为 ;
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由;
(3)在(2)的条件下,如图3,在∠BOE的内部是否存在一条射线OD,使得∠BOD为直角,且∠DOF=3∠DOE?若存在,请求出∠COF的度数;若不存在,请说明理由.
参考答案
一、1. B 2.C 3.C 4.C 5.C 6.A 7.C 8.B 9.D 10.C 二、11.(2),(5) 12.四棱锥 13.6 14.左视图 15.② 16.135 17.14或6 18.北偏东70°
三、19.解:如图所示:
.
20.解:(1)侧面积:2×4×5=40(cm2).
(2)共10个顶点,共有7个面,共有15条棱;
(3)n棱柱的顶点数2n;面数n+2;棱的条数3n.
21.解:(1)画图如下:
(2)最多可以再添加2个小正方体.故答案为:2.
22.解:∵∠BOC=2∠AOC,∠AOC=40°,
∴∠BOC=2×40°=80°,
∴∠AOB=∠BOC+∠AOC=80°+40°=120°,
∵OD平分∠AOB,
∴∠AOD=∠AOB=×120°=60°,
∴∠COD=∠AOD﹣∠AOC=60°﹣40°=20°.
23.解:(1)∵点M、N分别是AC、BC的中点,
∴MC=AC=×8cm=4cm,NC=BC=×6cm=3cm,
∴MN=MC+NC=4cm+3cm=7cm;
(2)MN=acm.理由如下:
∵点M、N分别是AC、BC的中点,
∴MC=AC,NC=BC,
∴MN=MC+NC=AC+BC=AB=acm;
(3)如图,
∵点M、N分别是AC、BC的中点,
∴MC=AC,NC=BC,
∴MN=MC﹣NC=AC﹣BC=(AC﹣BC)=bcm.
附加题:
24.解:(1)如图所示,有如下五种情况:
(2)∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;
由主视图可得第2层最多有4个正方体,第3层最多有2个正方体;
∴该组合几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,
∴n可能为8或9或10或11.
25.解:(1)∵∠AOE=∠AOB﹣∠BOE,OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
∵∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF,
当∠COF=14°时,∠BOE=28°;当∠COF=n°时,∠BOE=2n°,
故答案为28°;2n°;∠BOE=2∠COF.
(2)∠BOE=2∠COF仍然成立.理由如下:
∵∠AOE=∠AOB﹣∠BOE,OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
∵∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF;
(3)存在.
设∠AOF=∠EOF=2x,
∵∠DOF=3∠DOE,
∴∠DOE=x,
而∠BOD为直角,
∴2x+2x+x+90°=160°,
解得x=14°,
∴∠BOE=90°+x=104°,
∴∠COF=×104°=52°(满足∠COF+∠FOE=∠COE=80°).
一、选择题(每小题3分,共30分)
1.修建高速公路时,经常将弯曲的道路改直,从而缩短路程,这样做的数学根据是( )
A.两点确定一条直线 B.两点之间,线段最短
C.垂线段最短 D.同位角相等,两直线平行
2.下列说法正确的是( )
①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.
A.①② B.①③ C.②③ D.①②③
3.如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )
A.敬 B.业 C.诚 D.信
4.如图,点B、C、D依次在射线AP上,根据图示,下列线段长度错误的是( )
A.AD=2a B.BC=a﹣b C.BD=a﹣b D.AC=2a﹣b
5.如图所示为某几何体的示意图,该几何体的左视图应为( )
A. B. C. D.
6.已知∠α的补角为125°12′,则它的余角为( )
A.35°12′ B.35°48′ C.55°12′ D.55°48′
7.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有( )
A.1个 B.2个 C.3个 D.4个
8.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )
A.50° B.65° C.75° D.60°
9.如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
A.4 B.6 C.8 D.10
10.一个几何体由一些小正方体摆成,其主视图与左视图如图所示,其俯视图不可能( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.如图所示,按要求填写.其中多面体有: .
12.一个几何体的表面展开图如图所示,则这个几何体是 .
13.一个多边形有8条边,从其中的一个顶点出发,连接这个点和其他顶点,
可以得到 个三角形.
14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 .
15.如图,一长方体木板上有两个洞,一个是正方形形状的,一个是圆形形状的,对于以下4种几何体,你觉得哪一种作为塞子既可以堵住圆形空洞又可以堵住方形空洞? (填序号).
16.如图所示,∠AOB是平角,∠COD=90°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于 度.
17.已知A、B、C三点在同一直线上,线段AB=10,BC=4,则线段AC= .
18.如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是 .
三、解答题(5个小题,共46分)
19.(6分)如图,已知四个点A、B、C、D,根据下列要求画图:
(1)画线段AB;
(2)画∠CDB;
(3)延长AD、BC交于点P.
20.(8分)如图,一个正五棱柱的底面边长为2cm,高为4cm.
(1)计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少个面?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.
21.(10分)如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
22.(10分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°,求∠COD的度数.
23.(12分)如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=acm,其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣CB=bcm,M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
附加题:(每小题10分,共20分)
24.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
25.已知∠AOB=160°,∠COE=80°,OF平分∠AOE.
(1)如图1,若∠COF=14°,则∠BOE= ;若∠COF=n°,则∠BOE= ,∠BOE与∠COF的数量关系为 ;
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由;
(3)在(2)的条件下,如图3,在∠BOE的内部是否存在一条射线OD,使得∠BOD为直角,且∠DOF=3∠DOE?若存在,请求出∠COF的度数;若不存在,请说明理由.
参考答案
一、1. B 2.C 3.C 4.C 5.C 6.A 7.C 8.B 9.D 10.C 二、11.(2),(5) 12.四棱锥 13.6 14.左视图 15.② 16.135 17.14或6 18.北偏东70°
三、19.解:如图所示:
.
20.解:(1)侧面积:2×4×5=40(cm2).
(2)共10个顶点,共有7个面,共有15条棱;
(3)n棱柱的顶点数2n;面数n+2;棱的条数3n.
21.解:(1)画图如下:
(2)最多可以再添加2个小正方体.故答案为:2.
22.解:∵∠BOC=2∠AOC,∠AOC=40°,
∴∠BOC=2×40°=80°,
∴∠AOB=∠BOC+∠AOC=80°+40°=120°,
∵OD平分∠AOB,
∴∠AOD=∠AOB=×120°=60°,
∴∠COD=∠AOD﹣∠AOC=60°﹣40°=20°.
23.解:(1)∵点M、N分别是AC、BC的中点,
∴MC=AC=×8cm=4cm,NC=BC=×6cm=3cm,
∴MN=MC+NC=4cm+3cm=7cm;
(2)MN=acm.理由如下:
∵点M、N分别是AC、BC的中点,
∴MC=AC,NC=BC,
∴MN=MC+NC=AC+BC=AB=acm;
(3)如图,
∵点M、N分别是AC、BC的中点,
∴MC=AC,NC=BC,
∴MN=MC﹣NC=AC﹣BC=(AC﹣BC)=bcm.
附加题:
24.解:(1)如图所示,有如下五种情况:
(2)∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;
由主视图可得第2层最多有4个正方体,第3层最多有2个正方体;
∴该组合几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,
∴n可能为8或9或10或11.
25.解:(1)∵∠AOE=∠AOB﹣∠BOE,OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
∵∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF,
当∠COF=14°时,∠BOE=28°;当∠COF=n°时,∠BOE=2n°,
故答案为28°;2n°;∠BOE=2∠COF.
(2)∠BOE=2∠COF仍然成立.理由如下:
∵∠AOE=∠AOB﹣∠BOE,OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
∵∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF;
(3)存在.
设∠AOF=∠EOF=2x,
∵∠DOF=3∠DOE,
∴∠DOE=x,
而∠BOD为直角,
∴2x+2x+x+90°=160°,
解得x=14°,
∴∠BOE=90°+x=104°,
∴∠COF=×104°=52°(满足∠COF+∠FOE=∠COE=80°).
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
