华师大版七年级上册 第1章 走进数学世界 单元测试(含答案)
文档属性
| 名称 | 华师大版七年级上册 第1章 走进数学世界 单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 140.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 12:08:36 | ||
图片预览



文档简介
第1章《走进数学世界》单元测试
一、选择(每小题3分,共36分)
1.我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是( )
A.《九章算术》 B.《海岛算经》 C.《孙子算经》 D.《五经算术》
提示:根据数学常识解答即可.此著作是《九章算术》,故选A.
2.如图,“吋”是电视机常用尺寸,1吋约为大拇指第一节的长,则7吋长相当于( )
A.一支粉笔的长度 B.课桌的长度
C.黑板的宽度 D.数学课本的宽度
提示:根据题意可得1吋约为大拇指第一节的长,大约有3﹣﹣4厘米,所以7吋长相当于数学课本的宽度.故选D.
3.我区某中学为便于管理,决定给每个学生编号,设定末尾用1表示男生,2表示女生.如果编号0903231表示“2009年入学的3班23号学生,是位男生”,那么,2013年入学的10班21号女生同学的编号为( )
A.0310211 B.0310212 C.1310211 D.1310212
提示:根据前两位表示年,第二个两位表示班,第三个两位表示号,最后一位表示男女, 2013年入学的10班21号女生同学的编号为1310212,故选:D.
4.设想有一根铁丝套在地球的赤道上,刚好拉紧后,又放长了10米,并使得铁丝均匀地离开地面.则下面说法中比较合理的是( )
A.你只能塞过一张纸 B.只能伸进你的拳头
C.能钻过一只小羊 D.能驶过一艘万吨巨轮
提示:设地球的半径是R,铁丝均匀地离开地面的高度是h,由圆的周长公式有:
2π(R+h)=2πR+10,2πR+2πh=2πR+10,∴2πh=10,h=≈1.6米.根据纸的厚度,进行分析,应选C.故选:C.
5.下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是( )
A.上海自来水来自海上 B.有志者事竞成
C.清水池里池水清 D.蜜蜂酿蜂蜜
提示:A、上海自来水来自海上,可将“水”理解为对称轴,对折后重合的字相同,故本选项错误;
B、有志者事竞成,五字均不相同,所以不对称,故本选项正确;
C、清水池里池水清,可将“里”理解为对称轴,对折后重合的字相同,故本选项错误;
D、蜜蜂酿蜂蜜,可将“酿”理解为对称轴,对折后重合的字相同,故本选项错误.
故选B.
6.用三张扑克牌:黑桃2,黑桃5,黑桃7,可以排成不同的三位数的个数为( )
A.1个 B.2个
C.7个 D.以上答案都不对
提示:因为以2开头的为257,275,以5为开头为527,572,以7开头的为725,752,所以它们排成的三位数为6个.故选D.
7.如图,一副沛县的汽车牌照,苏代表江苏,C代表徐州,J代表沛县,当“C?J”后面的4个数位上都是数字时,最多可以供上牌的汽车数是( )
A.1000辆 B.10000辆 C.9999辆 D.9000辆
提示:∵当“C?J”后面的4个数位上都是数字时,∴从0000到9999,故最多可以供上牌的汽车数是:10000辆.故选:B.
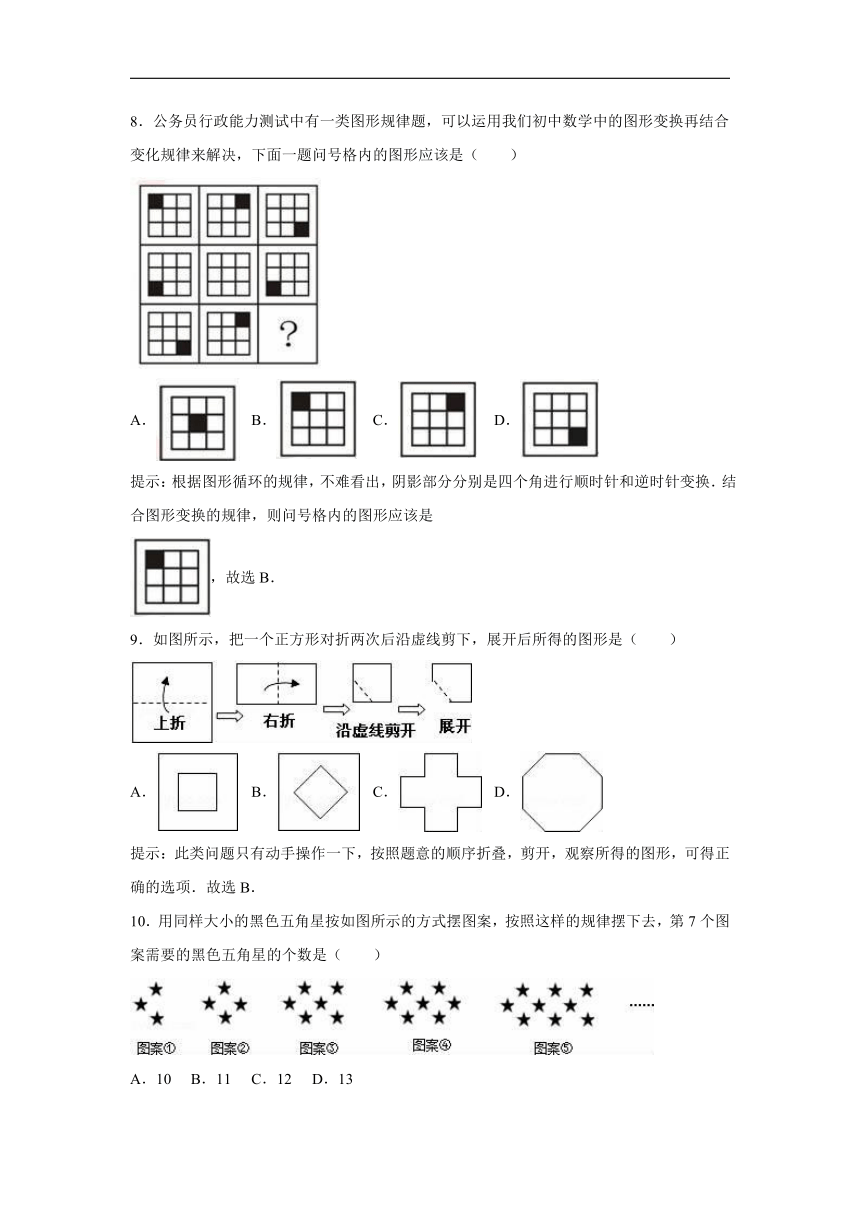
8.公务员行政能力测试中有一类图形规律题,可以运用我们初中数学中的图形变换再结合变化规律来解决,下面一题问号格内的图形应该是( )
A. B. C. D.
提示:根据图形循环的规律,不难看出,阴影部分分别是四个角进行顺时针和逆时针变换.结合图形变换的规律,则问号格内的图形应该是
,故选B.
9.如图所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是( )
A. B. C. D.
提示:此类问题只有动手操作一下,按照题意的顺序折叠,剪开,观察所得的图形,可得正确的选项.故选B.
10.用同样大小的黑色五角星按如图所示的方式摆图案,按照这样的规律摆下去,第7个图案需要的黑色五角星的个数是( )
A.10 B.11 C.12 D.13
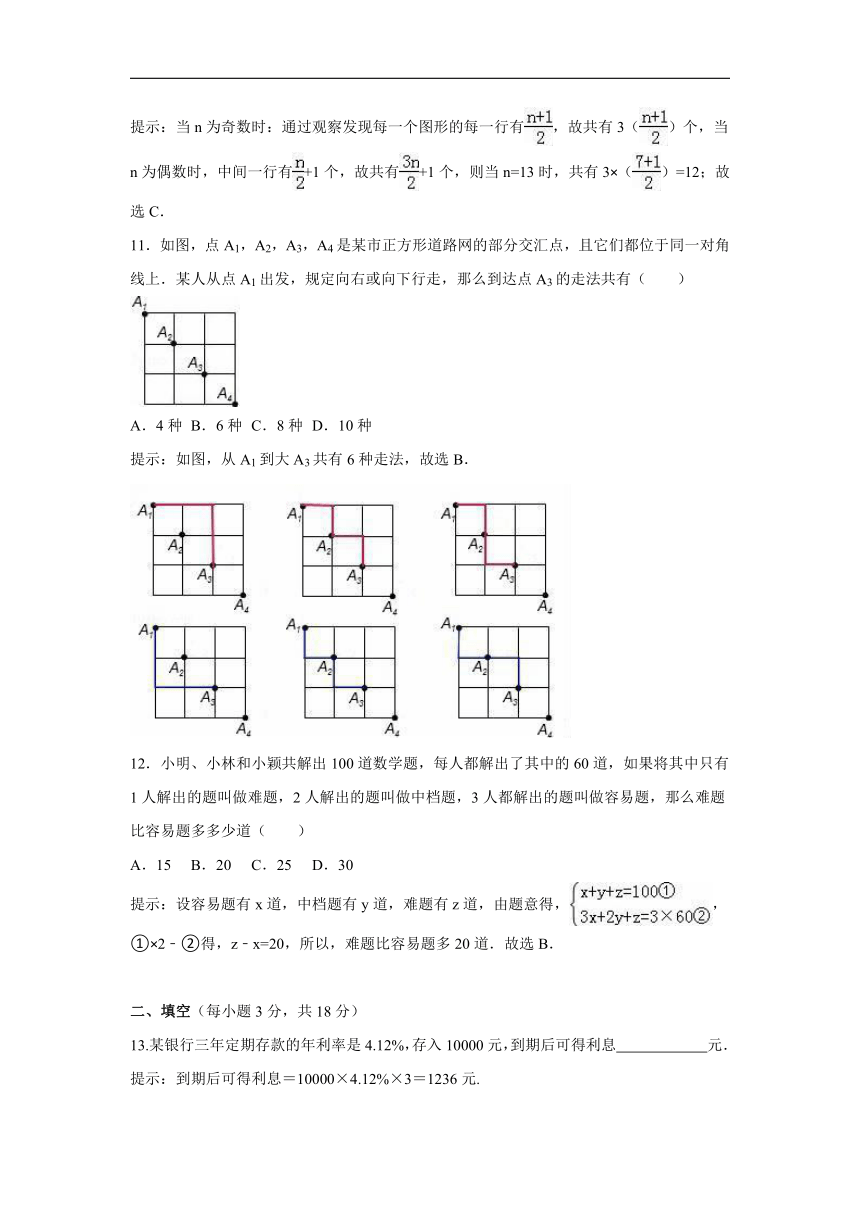
提示:当n为奇数时:通过观察发现每一个图形的每一行有,故共有3()个,当n为偶数时,中间一行有+1个,故共有+1个,则当n=13时,共有3×()=12;故选C.
11.如图,点A1,A2,A3,A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有( )
A.4种 B.6种 C.8种 D.10种
提示:如图,从A1到大A3共有6种走法,故选B.
12.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
提示:设容易题有x道,中档题有y道,难题有z道,由题意得,,①×2﹣②得,z﹣x=20,所以,难题比容易题多20道.故选B.
二、填空(每小题3分,共18分)
13.某银行三年定期存款的年利率是4.12%,存入10000元,到期后可得利息 元.
提示:到期后可得利息=10000×4.12%×3=1236元.
14.测量1张纸大约有多厚,出现了以下四种观点,
①直接用三角尺测量1张纸的厚度;
②先用三角尺测量同类型的2张纸的厚度;
③先用三角尺测量同类型的50张纸的厚度;
④先用三角尺测量同类型的100000张纸的厚度
你认为最合理且可行的观点是 .
提示:A、一张纸的厚度不易测出,错误;B、2张纸的厚度不易测出,错误;
C、正确;D、100 000张数据太大,错误.故选③.
15.猜谜语:(1)0 1 2 5 6 7 8 9 (打一成语) ;
(2)你等着我,我等着你(打一数学名词) .
提示:(1)观察数字,少了3和4,显然是丢三落四;(2)显然是互相等待,即相等.故答案为:(1)丢三落四;(2)相等.
16.如图,三角形共有 个.
提示:第一条横线上的有6个,第二条横线上的也有6个,共有12个.故答案为:12.
17.如图是某班同学对新闻、动画、娱乐、戏曲五类最喜爱电视节目的条形统计图,根据条形统计图可得出该班最喜爱娱乐节目的人数占全班人数的百分比是 .
提示:该班最喜爱娱乐节目的人数占全班人数的百分比=×100%=36%.
故答案为36%.
18.小聪,小玲,小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,试问:这五道题的正确答案(按1~5题的顺序排列)是 .
题号
答案
选手
1
2
3
4
5
得分
小聪
B
A
A
B
A
40
小玲
B
A
B
A
A
40
小红
A
B
B
B
A
30
提示:根据得分可得小聪和小玲都是只有一个错,小红有2个错误.
第5题,三人选项相同,若不是选A,则小聪和小玲的其它题目的答案一定相同,与已知矛盾,则第5题的答案是A;
第3个第4题小聪和小玲都不同,则一定在这两题上其中一人有错误,则第1,2正确,则1的答案是:B,2的答案是:A;
则小红的错题是1和2,则3和4正确,则3的答案是:B,4的答案是:B.
总之,正确答案(按1~5题的顺序排列)是BABBA.
故答案是:BABBA.
三、解答(8个小题,共66分)
19.某市消费者协会在“3?15”期间的一周内,将接到的热线电话绘成如图所示的统计图,其中关于环境保护问题的电话共有70个,根据统计图回答下列问题:
(1)本周热线电话共有多少个?
(2)有关表扬建议的电话有多少个?
思路分析:(1)有环境保护的问题的电话个数除以占的百分比即可求出本周热线电话的总数;(2)根据表扬建议所占的百分比乘以总个数,即可求出表扬建议的电话数.
解:(1)由统计图可知,关于环境保护的问题电话有70个,占热线电话总数的35%,
则热线电话总数为70÷35%=200(个);
(2)有关表扬建议的电话占热线电话总数的10%,即有200×10%=20(个).
20.希望小学学生王晶和他的爸爸、妈妈准备在“元旦”期间外出旅游.阳光旅行社的收费标准为:大人全价,小孩半价;而蓝天旅行社不管大人小孩,一律八折.这两家旅行社的基本费一样,都是300元,你认为应该去哪家旅行社较为合算?为什么?
思路分析:先分别计算出阳光旅行社的收费和蓝天旅行社的收费作比较,再确定哪家旅行社较为合算.
解:阳光旅行社的收费为:2×300+150=750(元);
蓝天旅行社的收费为:300×0.8×3=720(元).
因为720<750,
所以应该去蓝天旅行社较为合算.
21.已知12人乘车去某地,可供租的车辆有两种:一种车可乘8人,另一种车可乘4人.
(1)请给出3种以上的租车方案;
(2)如果第一种车的租金是300元/天,第二种车的租金是200元/天,那么采用哪种方案费用最少?
思路分析:(1)都乘8人座的;都乘4人座的;也乘8人座,也乘4人座;(2)结合(1)进行解答.
解:(1)都乘8人座的,12÷8=1…4,需2辆;
都乘4人座的,12÷4=3,需3辆;
也乘8人座,也乘4人座,8+4=12,需一辆8人座,一辆4人座.
(2)都乘8人座的,需付费:2×300=600元;
都乘4人座的,需付费:3×200=600元;
也乘8人座,也乘4人座,需付费:300+200=500元.
故一辆8人座,一辆4人座费用最少.
22.温度的变化是人们经常谈论的话题,请根据下图与同伴讨论某地某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
思路分析:(1)观察图象,可知最高温度为37℃,时间为15时,最低温度是23℃;
(2)由(1)中得出的最高温度﹣最低温度即可求出温差,也可求得经过的时间;
(3)观察图象可求解.
解:(1)根据图象可以看出:
这一天的最高温度是37℃,是在15时到达的,
最低温度是23℃,是在3时达到的;
(2)温差为:37﹣23=14(℃),
经过的时间为:15﹣3=12(时);
(3)从3时到15时温度在上升,在0时到3时、15时到24时温度在下降.
23.在3×3的方格纸中(如图),试用格点连线将方格纸分割成两个全等的多边形(指形状相同,大小相等的多边形),如图就是其中一例,各格点分别是A(0,3),B(2,2),C(1,1),D(3,0)顺次连接这些点,即把方格纸分割成两个全等多边形.
(1)你还能想出哪些分割方法?
(2)你发现了哪些规律有助你找到更多的答案?
思路分析:(1)可以仿照例子中的点给出,或根据正方形的对角线平分正方形给出;
(2)依据写出的点的位置关系可以写出.
解:(1)顺次连接(3,3),(1,2),(2,1),(0,0).
或顺次连接(0,0)(1,1)(2,2)(3,3).(答案不唯一).
(2)四个点一定是关于正方形的中心(1.5,1.5)对称的两组点.
24.如图,表2、表3是从表1中截取的一部分,求a+b的值.
表1
1
2
3
4
…
2
4
6
8
…
3
6
9
12
…
4
8
12
16
…
…
…
…
…
…
表2
15
24
a
表3
16
24
b
思路分析:求a的值时,分15是5的3倍和15是3的5倍两种情况;求b的值时,分16是8的2倍,2的8倍和4的4倍三种情况讨论.
解:根据表1中数据规律可知:横排中1,2,3,4…对应的竖排中数据都是第1个数的倍数,由上往下依次是1倍,2倍,3倍…,
表2中,当15是5的3倍时,24是6的4倍,所以a是6的5倍,即30,当15是3的5倍时,24是4的6倍,所以a是4的7倍,即28;
当16是8的2倍时,24是8的3倍,所以b是7的4倍,即28,当16是2的8倍时,16的正下方应是2的9倍即18,与题意不符;当16是4的4倍时,16的正下方应为4的5倍是20,与题意不符.
所以a+b=30+28=58,或者28+28=56.
25.大冠买了一包宣纸练习书法,每星期一写1张,每星期二写2张,每星期三写3张,每星期四写4张,每星期五写5张,每星期六写6张,每星期日写7张.若大冠从某年的5月1日开始练习,到5月30日练习完后累积写完的宣纸总数已超过120张,则5月30日可能为星期几?请求出所有可能的答案并完整说明理由.
思路分析:首先得出5月1日~5月30日,包括四个完整的星期,分别分析5月30日当分别为星期一到星期天时所有的可能,进而得出答案.
解:∵5月1日~5月30日共30天,包括四个完整的星期,
∴5月1日~5月28日写的张数为:4×=112,
若5月30日为星期一,所写张数为112+7+1=120,
若5月30日为星期二,所写张数为112+1+2<120,
若5月30日为星期三,所写张数为112+2+3<120,
若5月30日为星期四,所写张数为112+3+4<120,
若5月30日为星期五,所写张数为112+4+5>120,
若5月30日为星期六,所写张数为112+5+6>120,
若5月30日为星期日,所写张数为112+6+7>120,
故5月30日可能为星期五、六、日.
26.生活与数学:(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是 ;
(2)玛丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是 ;
(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是 ;
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号;
(5)若干个偶数按每行8个数排成下图:
①图中方框内的9个数的和与中间的数有什么关系?
②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是 ;
③托马斯也画了一个斜框,斜框内9个数的和为270,则斜框的中间一个数是 .
思路分析:先根据日历上的数据规律把所要求的数用代数式表示,用方程求解即可.
解:(1)设第一个数是x,其他的数为x+1,x+7,x+8,
则x+x+1+x+7+x+8=32,
解得x=4;
(2)设第一个数是x,其他的数为x+1,x+6,x+7,
则x+x+1+x+6+x+7=42,
解得x=7.
x+1=8,x+6=13,x+7=14;
(3)设中间的数是x,
则5x=50,
解得x=10;
(4)设最后一个星期日是x,x﹣7,x﹣14,x﹣21,x﹣28,
则x+x﹣7+x﹣14+x﹣21+x﹣28=75,
解得x=29;
(5)①和是中间的数的9倍.
②根据规律可知,和是中间的数的9倍,
设中间的数是x,
则9x=360,
解得x=40.
③设中间的数是x,
则9x=270,
解得x=30.
一、选择(每小题3分,共36分)
1.我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是( )
A.《九章算术》 B.《海岛算经》 C.《孙子算经》 D.《五经算术》
提示:根据数学常识解答即可.此著作是《九章算术》,故选A.
2.如图,“吋”是电视机常用尺寸,1吋约为大拇指第一节的长,则7吋长相当于( )
A.一支粉笔的长度 B.课桌的长度
C.黑板的宽度 D.数学课本的宽度
提示:根据题意可得1吋约为大拇指第一节的长,大约有3﹣﹣4厘米,所以7吋长相当于数学课本的宽度.故选D.
3.我区某中学为便于管理,决定给每个学生编号,设定末尾用1表示男生,2表示女生.如果编号0903231表示“2009年入学的3班23号学生,是位男生”,那么,2013年入学的10班21号女生同学的编号为( )
A.0310211 B.0310212 C.1310211 D.1310212
提示:根据前两位表示年,第二个两位表示班,第三个两位表示号,最后一位表示男女, 2013年入学的10班21号女生同学的编号为1310212,故选:D.
4.设想有一根铁丝套在地球的赤道上,刚好拉紧后,又放长了10米,并使得铁丝均匀地离开地面.则下面说法中比较合理的是( )
A.你只能塞过一张纸 B.只能伸进你的拳头
C.能钻过一只小羊 D.能驶过一艘万吨巨轮
提示:设地球的半径是R,铁丝均匀地离开地面的高度是h,由圆的周长公式有:
2π(R+h)=2πR+10,2πR+2πh=2πR+10,∴2πh=10,h=≈1.6米.根据纸的厚度,进行分析,应选C.故选:C.
5.下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是( )
A.上海自来水来自海上 B.有志者事竞成
C.清水池里池水清 D.蜜蜂酿蜂蜜
提示:A、上海自来水来自海上,可将“水”理解为对称轴,对折后重合的字相同,故本选项错误;
B、有志者事竞成,五字均不相同,所以不对称,故本选项正确;
C、清水池里池水清,可将“里”理解为对称轴,对折后重合的字相同,故本选项错误;
D、蜜蜂酿蜂蜜,可将“酿”理解为对称轴,对折后重合的字相同,故本选项错误.
故选B.
6.用三张扑克牌:黑桃2,黑桃5,黑桃7,可以排成不同的三位数的个数为( )
A.1个 B.2个
C.7个 D.以上答案都不对
提示:因为以2开头的为257,275,以5为开头为527,572,以7开头的为725,752,所以它们排成的三位数为6个.故选D.
7.如图,一副沛县的汽车牌照,苏代表江苏,C代表徐州,J代表沛县,当“C?J”后面的4个数位上都是数字时,最多可以供上牌的汽车数是( )
A.1000辆 B.10000辆 C.9999辆 D.9000辆
提示:∵当“C?J”后面的4个数位上都是数字时,∴从0000到9999,故最多可以供上牌的汽车数是:10000辆.故选:B.
8.公务员行政能力测试中有一类图形规律题,可以运用我们初中数学中的图形变换再结合变化规律来解决,下面一题问号格内的图形应该是( )
A. B. C. D.
提示:根据图形循环的规律,不难看出,阴影部分分别是四个角进行顺时针和逆时针变换.结合图形变换的规律,则问号格内的图形应该是
,故选B.
9.如图所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是( )
A. B. C. D.
提示:此类问题只有动手操作一下,按照题意的顺序折叠,剪开,观察所得的图形,可得正确的选项.故选B.
10.用同样大小的黑色五角星按如图所示的方式摆图案,按照这样的规律摆下去,第7个图案需要的黑色五角星的个数是( )
A.10 B.11 C.12 D.13
提示:当n为奇数时:通过观察发现每一个图形的每一行有,故共有3()个,当n为偶数时,中间一行有+1个,故共有+1个,则当n=13时,共有3×()=12;故选C.
11.如图,点A1,A2,A3,A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有( )
A.4种 B.6种 C.8种 D.10种
提示:如图,从A1到大A3共有6种走法,故选B.
12.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
提示:设容易题有x道,中档题有y道,难题有z道,由题意得,,①×2﹣②得,z﹣x=20,所以,难题比容易题多20道.故选B.
二、填空(每小题3分,共18分)
13.某银行三年定期存款的年利率是4.12%,存入10000元,到期后可得利息 元.
提示:到期后可得利息=10000×4.12%×3=1236元.
14.测量1张纸大约有多厚,出现了以下四种观点,
①直接用三角尺测量1张纸的厚度;
②先用三角尺测量同类型的2张纸的厚度;
③先用三角尺测量同类型的50张纸的厚度;
④先用三角尺测量同类型的100000张纸的厚度
你认为最合理且可行的观点是 .
提示:A、一张纸的厚度不易测出,错误;B、2张纸的厚度不易测出,错误;
C、正确;D、100 000张数据太大,错误.故选③.
15.猜谜语:(1)0 1 2 5 6 7 8 9 (打一成语) ;
(2)你等着我,我等着你(打一数学名词) .
提示:(1)观察数字,少了3和4,显然是丢三落四;(2)显然是互相等待,即相等.故答案为:(1)丢三落四;(2)相等.
16.如图,三角形共有 个.
提示:第一条横线上的有6个,第二条横线上的也有6个,共有12个.故答案为:12.
17.如图是某班同学对新闻、动画、娱乐、戏曲五类最喜爱电视节目的条形统计图,根据条形统计图可得出该班最喜爱娱乐节目的人数占全班人数的百分比是 .
提示:该班最喜爱娱乐节目的人数占全班人数的百分比=×100%=36%.
故答案为36%.
18.小聪,小玲,小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,试问:这五道题的正确答案(按1~5题的顺序排列)是 .
题号
答案
选手
1
2
3
4
5
得分
小聪
B
A
A
B
A
40
小玲
B
A
B
A
A
40
小红
A
B
B
B
A
30
提示:根据得分可得小聪和小玲都是只有一个错,小红有2个错误.
第5题,三人选项相同,若不是选A,则小聪和小玲的其它题目的答案一定相同,与已知矛盾,则第5题的答案是A;
第3个第4题小聪和小玲都不同,则一定在这两题上其中一人有错误,则第1,2正确,则1的答案是:B,2的答案是:A;
则小红的错题是1和2,则3和4正确,则3的答案是:B,4的答案是:B.
总之,正确答案(按1~5题的顺序排列)是BABBA.
故答案是:BABBA.
三、解答(8个小题,共66分)
19.某市消费者协会在“3?15”期间的一周内,将接到的热线电话绘成如图所示的统计图,其中关于环境保护问题的电话共有70个,根据统计图回答下列问题:
(1)本周热线电话共有多少个?
(2)有关表扬建议的电话有多少个?
思路分析:(1)有环境保护的问题的电话个数除以占的百分比即可求出本周热线电话的总数;(2)根据表扬建议所占的百分比乘以总个数,即可求出表扬建议的电话数.
解:(1)由统计图可知,关于环境保护的问题电话有70个,占热线电话总数的35%,
则热线电话总数为70÷35%=200(个);
(2)有关表扬建议的电话占热线电话总数的10%,即有200×10%=20(个).
20.希望小学学生王晶和他的爸爸、妈妈准备在“元旦”期间外出旅游.阳光旅行社的收费标准为:大人全价,小孩半价;而蓝天旅行社不管大人小孩,一律八折.这两家旅行社的基本费一样,都是300元,你认为应该去哪家旅行社较为合算?为什么?
思路分析:先分别计算出阳光旅行社的收费和蓝天旅行社的收费作比较,再确定哪家旅行社较为合算.
解:阳光旅行社的收费为:2×300+150=750(元);
蓝天旅行社的收费为:300×0.8×3=720(元).
因为720<750,
所以应该去蓝天旅行社较为合算.
21.已知12人乘车去某地,可供租的车辆有两种:一种车可乘8人,另一种车可乘4人.
(1)请给出3种以上的租车方案;
(2)如果第一种车的租金是300元/天,第二种车的租金是200元/天,那么采用哪种方案费用最少?
思路分析:(1)都乘8人座的;都乘4人座的;也乘8人座,也乘4人座;(2)结合(1)进行解答.
解:(1)都乘8人座的,12÷8=1…4,需2辆;
都乘4人座的,12÷4=3,需3辆;
也乘8人座,也乘4人座,8+4=12,需一辆8人座,一辆4人座.
(2)都乘8人座的,需付费:2×300=600元;
都乘4人座的,需付费:3×200=600元;
也乘8人座,也乘4人座,需付费:300+200=500元.
故一辆8人座,一辆4人座费用最少.
22.温度的变化是人们经常谈论的话题,请根据下图与同伴讨论某地某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
思路分析:(1)观察图象,可知最高温度为37℃,时间为15时,最低温度是23℃;
(2)由(1)中得出的最高温度﹣最低温度即可求出温差,也可求得经过的时间;
(3)观察图象可求解.
解:(1)根据图象可以看出:
这一天的最高温度是37℃,是在15时到达的,
最低温度是23℃,是在3时达到的;
(2)温差为:37﹣23=14(℃),
经过的时间为:15﹣3=12(时);
(3)从3时到15时温度在上升,在0时到3时、15时到24时温度在下降.
23.在3×3的方格纸中(如图),试用格点连线将方格纸分割成两个全等的多边形(指形状相同,大小相等的多边形),如图就是其中一例,各格点分别是A(0,3),B(2,2),C(1,1),D(3,0)顺次连接这些点,即把方格纸分割成两个全等多边形.
(1)你还能想出哪些分割方法?
(2)你发现了哪些规律有助你找到更多的答案?
思路分析:(1)可以仿照例子中的点给出,或根据正方形的对角线平分正方形给出;
(2)依据写出的点的位置关系可以写出.
解:(1)顺次连接(3,3),(1,2),(2,1),(0,0).
或顺次连接(0,0)(1,1)(2,2)(3,3).(答案不唯一).
(2)四个点一定是关于正方形的中心(1.5,1.5)对称的两组点.
24.如图,表2、表3是从表1中截取的一部分,求a+b的值.
表1
1
2
3
4
…
2
4
6
8
…
3
6
9
12
…
4
8
12
16
…
…
…
…
…
…
表2
15
24
a
表3
16
24
b
思路分析:求a的值时,分15是5的3倍和15是3的5倍两种情况;求b的值时,分16是8的2倍,2的8倍和4的4倍三种情况讨论.
解:根据表1中数据规律可知:横排中1,2,3,4…对应的竖排中数据都是第1个数的倍数,由上往下依次是1倍,2倍,3倍…,
表2中,当15是5的3倍时,24是6的4倍,所以a是6的5倍,即30,当15是3的5倍时,24是4的6倍,所以a是4的7倍,即28;
当16是8的2倍时,24是8的3倍,所以b是7的4倍,即28,当16是2的8倍时,16的正下方应是2的9倍即18,与题意不符;当16是4的4倍时,16的正下方应为4的5倍是20,与题意不符.
所以a+b=30+28=58,或者28+28=56.
25.大冠买了一包宣纸练习书法,每星期一写1张,每星期二写2张,每星期三写3张,每星期四写4张,每星期五写5张,每星期六写6张,每星期日写7张.若大冠从某年的5月1日开始练习,到5月30日练习完后累积写完的宣纸总数已超过120张,则5月30日可能为星期几?请求出所有可能的答案并完整说明理由.
思路分析:首先得出5月1日~5月30日,包括四个完整的星期,分别分析5月30日当分别为星期一到星期天时所有的可能,进而得出答案.
解:∵5月1日~5月30日共30天,包括四个完整的星期,
∴5月1日~5月28日写的张数为:4×=112,
若5月30日为星期一,所写张数为112+7+1=120,
若5月30日为星期二,所写张数为112+1+2<120,
若5月30日为星期三,所写张数为112+2+3<120,
若5月30日为星期四,所写张数为112+3+4<120,
若5月30日为星期五,所写张数为112+4+5>120,
若5月30日为星期六,所写张数为112+5+6>120,
若5月30日为星期日,所写张数为112+6+7>120,
故5月30日可能为星期五、六、日.
26.生活与数学:(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是 ;
(2)玛丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是 ;
(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是 ;
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号;
(5)若干个偶数按每行8个数排成下图:
①图中方框内的9个数的和与中间的数有什么关系?
②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是 ;
③托马斯也画了一个斜框,斜框内9个数的和为270,则斜框的中间一个数是 .
思路分析:先根据日历上的数据规律把所要求的数用代数式表示,用方程求解即可.
解:(1)设第一个数是x,其他的数为x+1,x+7,x+8,
则x+x+1+x+7+x+8=32,
解得x=4;
(2)设第一个数是x,其他的数为x+1,x+6,x+7,
则x+x+1+x+6+x+7=42,
解得x=7.
x+1=8,x+6=13,x+7=14;
(3)设中间的数是x,
则5x=50,
解得x=10;
(4)设最后一个星期日是x,x﹣7,x﹣14,x﹣21,x﹣28,
则x+x﹣7+x﹣14+x﹣21+x﹣28=75,
解得x=29;
(5)①和是中间的数的9倍.
②根据规律可知,和是中间的数的9倍,
设中间的数是x,
则9x=360,
解得x=40.
③设中间的数是x,
则9x=270,
解得x=30.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
