第13章 全等三角形 单元检测题(含答案)
文档属性
| 名称 | 第13章 全等三角形 单元检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 70.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 15:22:12 | ||
图片预览



文档简介
第13章 全等三角形
一.选择题(共9小题)
1.下列命题中,是真命题的是( )
A.直线是有长度的线 B.两个数的绝对值一定不相等
C.相等的角一定是对顶角 D.整数是有理数
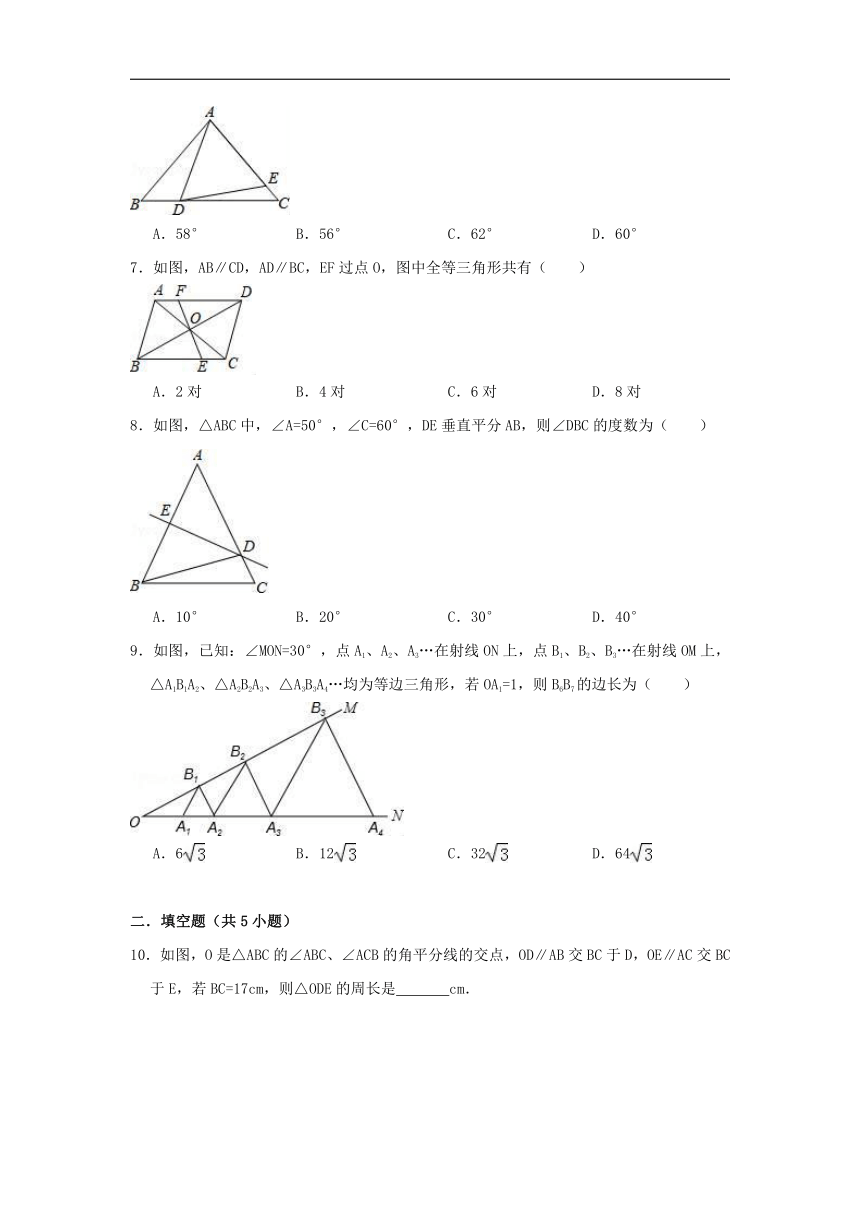
2.如图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC为( )
A.10 B.8 C.12 D.9
3.如图,等边△ABC的周长为18,且AD⊥BC于点D,那么AD的长为( )
A.3 B.4 C.3 D.6
4.下列命题是真命题的个数是( )
①对顶角相等,两直线平行; ②两直线平行,内错角相等;③同旁内角互补,两直线平行;④同位角相等,两直线平行;⑤1的平方根是1;⑥﹣8的立方根±2.
A.2 B.3 C.4 D.5
5.如图,△ABC≌△EBD,AB=4cm,BD=7cm,则CE的长度为( )
A.1cm B.2cm C.3cm D.4cm
6.如图,△ABC中,AB=AC,AD=DE,∠BAD=18°,∠EDC=12°,则∠DAE的度数为( )
A.58° B.56° C.62° D.60°
7.如图,AB∥CD,AD∥BC,EF过点O,图中全等三角形共有( )
A.2对 B.4对 C.6对 D.8对
8.如图,△ABC中,∠A=50°,∠C=60°,DE垂直平分AB,则∠DBC的度数为( )
A.10° B.20° C.30° D.40°
9.如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6 B.12 C.32 D.64
二.填空题(共5小题)
10.如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=17cm,则△ODE的周长是 cm.
11.如图,O为直线AB上一点,∠AOC的平分线是OM,∠BOC的平分线是ON,则∠MON的度数为 .
12.如图,点A,E,F,C在同一直线上,AB∥CD,BF∥DE,BF=DE,且AE=2,AC=8,则EF= .
13.张老师把红、白、蓝各一个气球分别送给三个小朋友.根据下面三句话,请你猜一猜,他们分到的各是什么颜色的气球?
(1)小春说:“我分到的不是蓝气球.”
(2)小宇说:“我分到的不是白气球.”
(3)小华说:“我看见张老师把蓝气球和红气球分给上面两位小朋友了.”
则小春、小宇、小华分别分到 颜色的气球.
14.在△ABC中,BA=BC,AC=14,S△ABC=84,D为AB上一动点,连接CD,过A作AE⊥CD与点E,连接BE,则BE的最小值是 .
三.解答题(共5小题)
15.如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=∠AOE,求∠AOC的度数;
(2)若∠BOC﹣∠AOC=72°,则OB与OC有怎样的位置关系?为什么?
16.已知一个等腰三角形的三边长分别为2x﹣1、x+1、3x﹣2,求这个等腰三角形的周长.
(1)完成部分解题过程,在以下解答过程的空白处填上适当的内容.
解:①当2x﹣1=x+1时,解x= ,此时 构成三角形(填“能”或“不能”).
②当2x﹣1=3x﹣2时,解x= ,此时 构成三角形(填“能”或“不能”).
(2)请你根据(1)中两种情况的分类讨论,完成第三种情况的分析,若能构成等腰三角形,求出这个三角形的周长.
17.如图,△ABC为等腰三角形,AB=AC,∠D=∠E,∠BAD=∠CAE.
(1)写出一对全等的三角形:△ ≌△ ;
(2)证明(1)中的结论;
(3)求证:点G为BC的中点.
18.(1)如图1,在Rt△ABC中,∠ACB=90°,AB=13cm,BC=12cm,AC=5cm
①作出△ABC的高线CD;
②求CD的长.
(2)已知,如图2,△ABC中,∠ABC=26°,∠C=48°,BD⊥CA于点D,∠BAC的平分线EA交BD的延长线于点F,求∠F的度数.
19.如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.
(1)如图1,若∠AOB=120°,∠AOC=30°,求∠EOF的度数?
(2)如图2,若∠AOB=α,求∠EOF的度数,(用含α的式子表示
(3)若将题中的“平分”的条件改为“∠EOB=∠COB,∠COF=∠COA,且∠AOB=α,求∠EOF的度数,(用含α的式子表示)
参考答案
一.选择题
1.D.
2.A.
3.C.
4.B.
5.C.
6.B.
7.C.
8.B.
9.C.
二.填空题
10.17.
11.90°.
12.4.
13.红、蓝、白.
14.5.
三.解答题
15.解:(1)∵∠COE=∠AOE,
∴∠AOE=3∠COE,
∵OE是∠AOB的平分线,
∴∠AOB=2∠AOE=6∠COE,
∵∠AOB=180°,
∴∠COE=18°,
∴∠AOC=2∠COE=2×18°=36°;
(2)OB⊥OC,
设∠BOC=x°,则∠AOC=108°﹣x°,
∵∠BOC﹣∠AOC=72°,
∴x﹣(108﹣x)=72,
解得x=90,
∴∠BOC=90°,
∴OB⊥OC.
16.解:(1)①当2x﹣1=x+1时,解x=2,此时3,3,4,能构成三角形.
②当2x﹣1=3x﹣2时,解x=1,此时1,2,1不能构成三角形.
故答案为2,能,1,不能;
(2)③当x+1=3x﹣2,解得x=,此时2,,能构成三角形.
17.(1)解:结论:△ABE≌△ACD.
(2)证明:∵∠BAD=∠CAE,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD.
故答案为ABE,ACD.
(3)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴BF=CF,∵AB=AC,
∴AF垂直平分线段BC,
∴BG=GC,
∴点G为BC的中点
18.解:(1)①作出△ABC的高线CD如图所示:
②∵AC×BC=AB×CD,
∴AC×BC=AB×CD,
∵AB=13,BC=12,AC=5,
∴5×12=13×CD,
∴CD=.
(2)∵∠C+∠ABC+∠BAC=180°,
∴∠BAC=180°﹣∠C﹣∠ABC.
∵∠ABC=26°,∠C=48°,
∴∠BAC=180°﹣48°﹣26°=106°.
∵EA平分∠BAC,
∴∠EAC=∠BAC=53°,
∵BD⊥CA,
∴∠ADF=90°.
∴∠F+∠DAF=90°,
∵∠DAF=∠EAC=53°,
∴∠F=90°﹣∠DAF=90°﹣53°=37°.
19.解:(1)∵OF平分∠AOC,
∴∠COF=∠AOC=×30°=15°,
∵∠BOC=∠AOB﹣∠AOC=120°﹣30°=90°,OE平分∠BOC,
∴∠EOC=∠BOC=45°,
∴∠EOF=∠COF+∠EOC=60°;
(2)∵OF平分∠AOC,
∴∠COF=∠AOC,
同理,∠EOC=∠BOC,
∴∠EOF=∠COF+∠EOC
=∠AOC+∠BOC
=(∠AOC+∠BOC)
=∠AOB
=α;
(3)∵∠EOB=∠COB,
∴∠EOC=∠COB,
∴∠EOF=∠EOC+∠COF
=∠COB+∠COA
=∠BOC+∠AOC
=∠AOB
=α.
一.选择题(共9小题)
1.下列命题中,是真命题的是( )
A.直线是有长度的线 B.两个数的绝对值一定不相等
C.相等的角一定是对顶角 D.整数是有理数
2.如图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC为( )
A.10 B.8 C.12 D.9
3.如图,等边△ABC的周长为18,且AD⊥BC于点D,那么AD的长为( )
A.3 B.4 C.3 D.6
4.下列命题是真命题的个数是( )
①对顶角相等,两直线平行; ②两直线平行,内错角相等;③同旁内角互补,两直线平行;④同位角相等,两直线平行;⑤1的平方根是1;⑥﹣8的立方根±2.
A.2 B.3 C.4 D.5
5.如图,△ABC≌△EBD,AB=4cm,BD=7cm,则CE的长度为( )
A.1cm B.2cm C.3cm D.4cm
6.如图,△ABC中,AB=AC,AD=DE,∠BAD=18°,∠EDC=12°,则∠DAE的度数为( )
A.58° B.56° C.62° D.60°
7.如图,AB∥CD,AD∥BC,EF过点O,图中全等三角形共有( )
A.2对 B.4对 C.6对 D.8对
8.如图,△ABC中,∠A=50°,∠C=60°,DE垂直平分AB,则∠DBC的度数为( )
A.10° B.20° C.30° D.40°
9.如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6 B.12 C.32 D.64
二.填空题(共5小题)
10.如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=17cm,则△ODE的周长是 cm.
11.如图,O为直线AB上一点,∠AOC的平分线是OM,∠BOC的平分线是ON,则∠MON的度数为 .
12.如图,点A,E,F,C在同一直线上,AB∥CD,BF∥DE,BF=DE,且AE=2,AC=8,则EF= .
13.张老师把红、白、蓝各一个气球分别送给三个小朋友.根据下面三句话,请你猜一猜,他们分到的各是什么颜色的气球?
(1)小春说:“我分到的不是蓝气球.”
(2)小宇说:“我分到的不是白气球.”
(3)小华说:“我看见张老师把蓝气球和红气球分给上面两位小朋友了.”
则小春、小宇、小华分别分到 颜色的气球.
14.在△ABC中,BA=BC,AC=14,S△ABC=84,D为AB上一动点,连接CD,过A作AE⊥CD与点E,连接BE,则BE的最小值是 .
三.解答题(共5小题)
15.如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=∠AOE,求∠AOC的度数;
(2)若∠BOC﹣∠AOC=72°,则OB与OC有怎样的位置关系?为什么?
16.已知一个等腰三角形的三边长分别为2x﹣1、x+1、3x﹣2,求这个等腰三角形的周长.
(1)完成部分解题过程,在以下解答过程的空白处填上适当的内容.
解:①当2x﹣1=x+1时,解x= ,此时 构成三角形(填“能”或“不能”).
②当2x﹣1=3x﹣2时,解x= ,此时 构成三角形(填“能”或“不能”).
(2)请你根据(1)中两种情况的分类讨论,完成第三种情况的分析,若能构成等腰三角形,求出这个三角形的周长.
17.如图,△ABC为等腰三角形,AB=AC,∠D=∠E,∠BAD=∠CAE.
(1)写出一对全等的三角形:△ ≌△ ;
(2)证明(1)中的结论;
(3)求证:点G为BC的中点.
18.(1)如图1,在Rt△ABC中,∠ACB=90°,AB=13cm,BC=12cm,AC=5cm
①作出△ABC的高线CD;
②求CD的长.
(2)已知,如图2,△ABC中,∠ABC=26°,∠C=48°,BD⊥CA于点D,∠BAC的平分线EA交BD的延长线于点F,求∠F的度数.
19.如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.
(1)如图1,若∠AOB=120°,∠AOC=30°,求∠EOF的度数?
(2)如图2,若∠AOB=α,求∠EOF的度数,(用含α的式子表示
(3)若将题中的“平分”的条件改为“∠EOB=∠COB,∠COF=∠COA,且∠AOB=α,求∠EOF的度数,(用含α的式子表示)
参考答案
一.选择题
1.D.
2.A.
3.C.
4.B.
5.C.
6.B.
7.C.
8.B.
9.C.
二.填空题
10.17.
11.90°.
12.4.
13.红、蓝、白.
14.5.
三.解答题
15.解:(1)∵∠COE=∠AOE,
∴∠AOE=3∠COE,
∵OE是∠AOB的平分线,
∴∠AOB=2∠AOE=6∠COE,
∵∠AOB=180°,
∴∠COE=18°,
∴∠AOC=2∠COE=2×18°=36°;
(2)OB⊥OC,
设∠BOC=x°,则∠AOC=108°﹣x°,
∵∠BOC﹣∠AOC=72°,
∴x﹣(108﹣x)=72,
解得x=90,
∴∠BOC=90°,
∴OB⊥OC.
16.解:(1)①当2x﹣1=x+1时,解x=2,此时3,3,4,能构成三角形.
②当2x﹣1=3x﹣2时,解x=1,此时1,2,1不能构成三角形.
故答案为2,能,1,不能;
(2)③当x+1=3x﹣2,解得x=,此时2,,能构成三角形.
17.(1)解:结论:△ABE≌△ACD.
(2)证明:∵∠BAD=∠CAE,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD.
故答案为ABE,ACD.
(3)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴BF=CF,∵AB=AC,
∴AF垂直平分线段BC,
∴BG=GC,
∴点G为BC的中点
18.解:(1)①作出△ABC的高线CD如图所示:
②∵AC×BC=AB×CD,
∴AC×BC=AB×CD,
∵AB=13,BC=12,AC=5,
∴5×12=13×CD,
∴CD=.
(2)∵∠C+∠ABC+∠BAC=180°,
∴∠BAC=180°﹣∠C﹣∠ABC.
∵∠ABC=26°,∠C=48°,
∴∠BAC=180°﹣48°﹣26°=106°.
∵EA平分∠BAC,
∴∠EAC=∠BAC=53°,
∵BD⊥CA,
∴∠ADF=90°.
∴∠F+∠DAF=90°,
∵∠DAF=∠EAC=53°,
∴∠F=90°﹣∠DAF=90°﹣53°=37°.
19.解:(1)∵OF平分∠AOC,
∴∠COF=∠AOC=×30°=15°,
∵∠BOC=∠AOB﹣∠AOC=120°﹣30°=90°,OE平分∠BOC,
∴∠EOC=∠BOC=45°,
∴∠EOF=∠COF+∠EOC=60°;
(2)∵OF平分∠AOC,
∴∠COF=∠AOC,
同理,∠EOC=∠BOC,
∴∠EOF=∠COF+∠EOC
=∠AOC+∠BOC
=(∠AOC+∠BOC)
=∠AOB
=α;
(3)∵∠EOB=∠COB,
∴∠EOC=∠COB,
∴∠EOF=∠EOC+∠COF
=∠COB+∠COA
=∠BOC+∠AOC
=∠AOB
=α.
