人教版八年级数学下册第十八章平行四边形18.2矩形课件(3课时共73张)
文档属性
| 名称 | 人教版八年级数学下册第十八章平行四边形18.2矩形课件(3课时共73张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 23:03:57 | ||
图片预览



文档简介
(共73张PPT)
矩 形
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形
即:
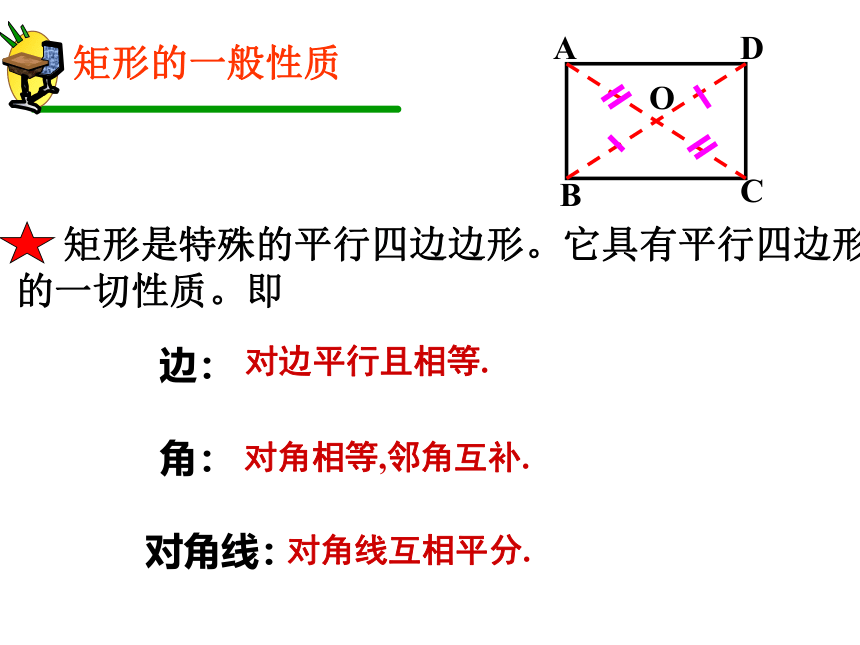
矩形是特殊的平行四边边形。它具有平行四边形
的一切性质。即
对边平行且相等.
对角相等,邻角互补.
对角线互相平分.
矩形的一般性质
边:
角:
对角线:
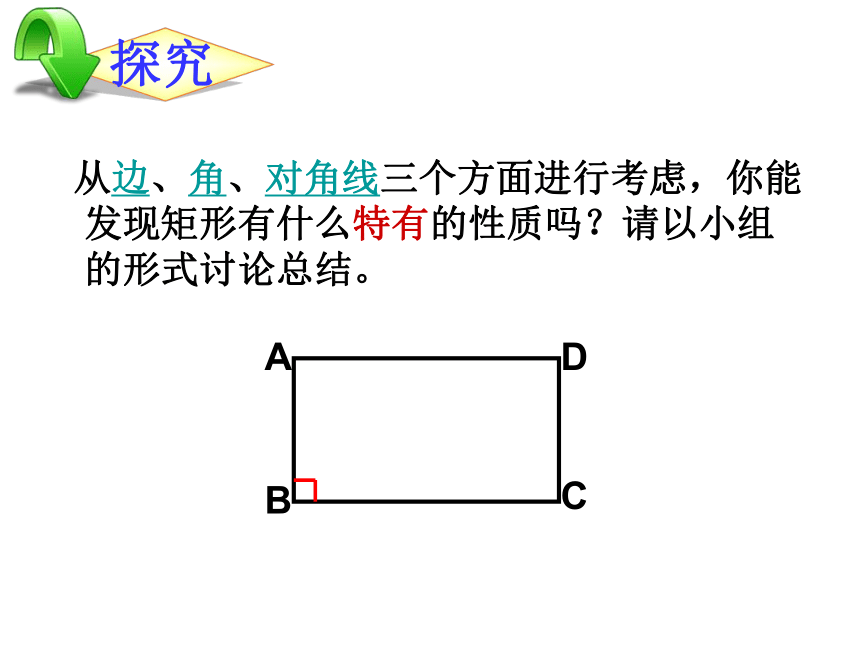
从边、角、对角线三个方面进行考虑,你能发现矩形有什么特有的性质吗?请以小组的形式讨论总结。
A
D
C
B
矩形的邻边垂直
A
B
C
D
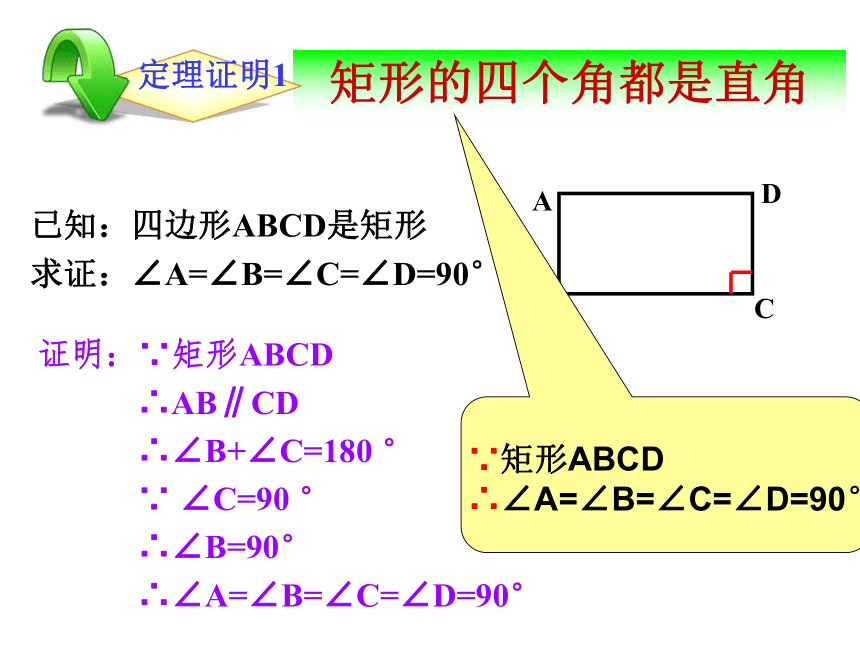
矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明:∵矩形ABCD
∴AB∥CD
∴∠B+∠C=180 °
∵ ∠C=90 °
∴∠B=90°
∴∠A=∠B=∠C=∠D=90°
定理证明1
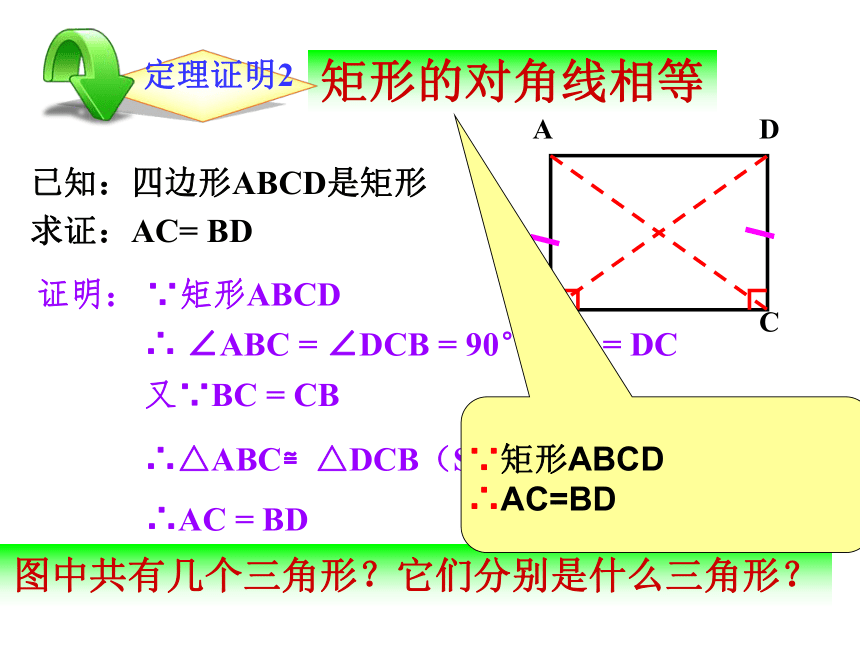
已知:四边形ABCD是矩形
求证:AC= BD
证明: ∵矩形ABCD
∴ ∠ABC = ∠DCB = 90°, AB = DC
又∵BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形的对角线相等
图中共有几个三角形?它们分别是什么三角形?
定理证明2
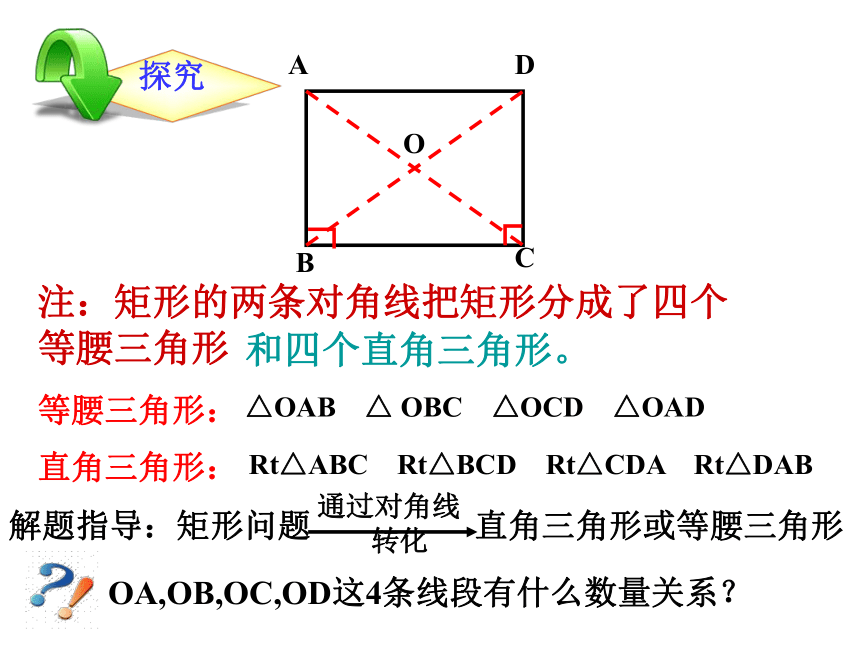
注:矩形的两条对角线把矩形分成了四个 等腰三角形
和四个直角三角形。
解题指导:矩形问题
直角三角形或等腰三角形
探究
等腰三角形:
△OAB △ OBC △OCD △OAD
直角三角形:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
O
OA,OB,OC,OD这4条线段有什么数量关系?
A
B
C
O
直角三角形斜边上的中线等于斜边的一半.
∵ 在Rt△ABC中, O是AC的中点,
∴BO= AC.
直角三角形的一个性质
几何语言:
(2)BO,AC分别是Rt△ABC的什么线段?
(3) BO与AC 有什么数量关系?为什么?
(4) 由此,你能得出什么结论?
(1)OA,OB,OC,OD这4条线段有什么数量关系?
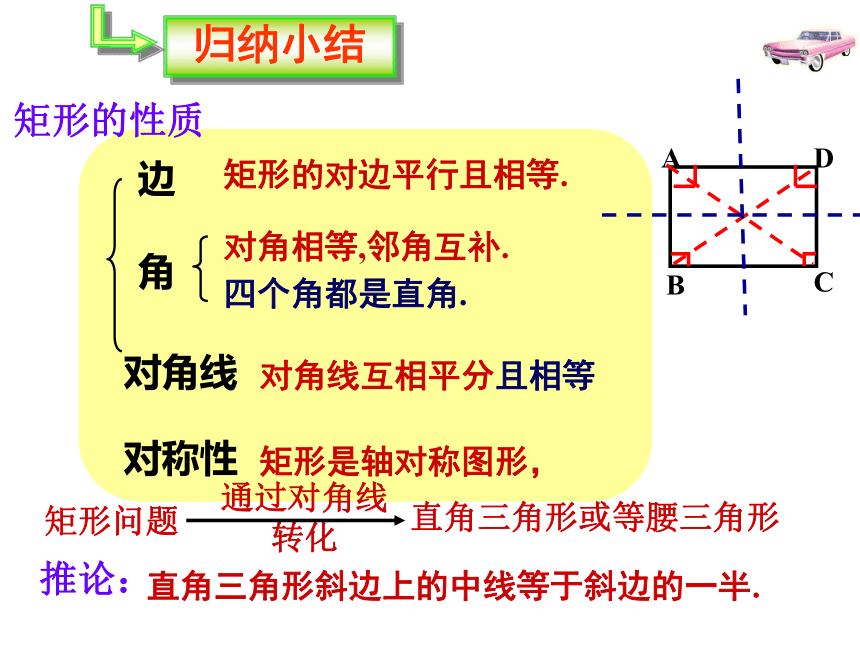
矩形的性质
A
B
C
D
矩形的对边平行且相等.
对角线互相平分且相等
对称性
矩形是轴对称图形,
推论:
直角三角形斜边上的中线等于斜边的一半.
矩形问题
直角三角形或等腰三角形
(1)矩形具有而平行四边形不具有的性质( )
A.内角和是360度 B.对角相等
C.对边平行且相等 D.对角线相等
(2)下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线垂直
D
D
(3)四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
(4)在Rt△ABC中, 两条直角边分别是6和8.则斜边上的
中线长为 。
5
A
O
B
C
(3)
(4)
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长?
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4
∴ AC=BD=2OA=8
解:∵ 矩形ABCD
方法小结: 如果矩形两对角线的夹角是60°
或120°, 则其中必有等边三角形.
∴ AC与BD相等且互相平分
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
O
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
又∵ 矩形ABCD
法一:
∴ AC与BD相等且互相平分
O
∴ OA=OB
∴ ∠CAB=∠1
证明:∵ AE∥BD
∴ ∠EAB=∠1
∴ ∠EAB=∠CBA
1
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
证明∵ 矩形ABCD
法二:
∴ AD∥EB ,
O
又∵ AE∥BD
∴ 四边形AEBD是平行四边形
∴ ∠EAB=∠CBA
∴ AE=BD
又∵ ∠ABC=90°
∴ AE=AC
(等腰三角形的三线合一)
AC=BD
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
证明∵ 矩形ABCD
法三:
∴ AD∥EB ,
O
又∵ AE∥BD
∴ 四边形AEBD是平行四边形
∴ △EAB≌△ CBA(SAS)
∴ AD=EB
又∵ ∠ABC=90°,AB=AB
∴ EB=BC
∴ ∠EAB=∠CBA
AD=BC
(1)知识结构图
(2)矩形不同于平行四边形的两条性质和推论
(3)解题指导:矩形问题
直角三角形或等腰三角形
(6)在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求矩形的周长及对角线的长
A
D
C
B
E
5
3
(4)在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AB= , AC=
B
C
D
E
A
O
4
2
1
1
(5)如图,在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求矩形的周长及对角线长。
5
3
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长?
变式:如图,矩形ABCD的两条对角线相交于点O,AC=8,求AB的长?
请你补充一个条件,使得问题可以解决。
(1)矩形具有而平行四边形不具有的性质( )
A.内角和是360度 B.对角相等
C.对边平行且相等 D.对角线相等
(2)下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线垂直
D
D
(3)已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 ( )
A.50° B.60° C.70° D.80°
D
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
矩形的特殊性质
有两组对边分别平行的四边形.
对边相等
邻边不相等
对角相等
邻角不相等
对边相等
邻边相等
对角相等
邻角相等
四条边都相等
四个角都相等
19.2特殊的平行四边形
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形
即:
生活中的矩形
矩形有什么性质?
有平行四边形的所有性质
还有其它特殊的性质
矩形的对边平行且相等.
矩形的对角相等.
矩形的对角线互相平分.
矩形的一般性质(即平行四边形所有性质)
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
矩形的特殊性质
矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
已知:四边形ABCD是矩形
求证:AC = BD
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形的对角线相等
矩形的性质
矩形的对边平行且相等.
对称性
矩形是轴对称图形,
也是中心对称图形.
A
B
C
O
直角三角形斜边上的中线等于斜边的一半.
在Rt△ABC中, BO是斜边AC上的中线,
则BO= AC.
直角三角形的一个性质
即:
D
证明: 延长BO至D,使OD=BO
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴AC=BD
在矩形ABCD中,找出相等的线段与相等的角.
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC
∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形:
△OAB △ OBC △OCD △OAD
直角三角形:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
在矩形ABCD中,找出所有等腰、直角、全等三角形.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长。
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
∴ OA=OB。
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长
AC=BD = 2OA=2×4=8(cm).
矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm。求AD的长及点A到BD的距离AE的长。
解:设AD=xcm,则对角线长(x+4)cm,在
Rt△ABD中,由勾股定理:
AD2+AB2=BD2 ∴
解得x=6。则 AD=6cm。
∵AE×DB= AD×AB
解得 AE= 4.8cm.
“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×DB= AD×AB
已知:矩形ABCD中,E是BC上一点,
DF⊥AE于F,若AE=BC.
求证:CE=EF。
脸蛋方方是矩形,例如黑板和窗门.
对角线段皆相等,相互交叉且平分.
内有直角三角形,斜边中线半斜边.
若要牢记其定义,直角平行四边形.
矩形之歌
矩形的定义:有一个角是直角的平行四边形.
矩形的性质:
具有平行四边形的一切特征.
四个角都是直角.
对角线相等且平分.
直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
1. 填空:
(1)矩形的定义中有两个条件:一是__________ ,
二是____________________ .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为____、____ 、 ____ 、 ____ 。
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为______ cm, ____ cm, ______ cm,____ cm。
有一个角是直角
平行四边形
60°
60°
120°
120°
5
5
2.下列说法错误的是( )
A. 矩形的对角线互相平分。
B. 矩形的对角线相等。
C. 有一个角是直角的四边形是矩形。
D. 有一个角是直角的平行四边形叫做矩形。
3. 矩形的对角线把矩形分成的三角形中全等三角形一共有( )
A. 2对 B. 4对 C. 6对 D. 8对
C
B
4. 工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是_________
______________
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边
框,当直角尺的两条直角边与窗框无缝隙时(如图4)
说明窗框合格,这时窗框是____,根据的数学道理
是_______________________
平行四边形
两组对边分别相等的
矩形
有一个角是直角的平行四边形是矩形
四边形是平行四边形
5. 用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
A. 48cm,12cm B. 48cm,16cm;
C. 44cm,16cm D. 45cm,15cm.
D
6. 四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
10. 小明想要做一个矩形像框,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?
1、理解并掌握矩形的判定方法。
2、能应用矩形定义、判定等知识,解决简单的证明题和计算题。
1.什么叫做平行四边形?什么叫做矩形?
2.矩形有哪些性质?
3.矩形与平行四边形有什么共同之处?有什么不同之处?
甲、乙、丙、丁四位同学到木工厂参观时,一木工师傅要他们利用自己所学的几何知识帮助检测一个窗框ABCD是不是矩形,他们各自做了检测。你认为他们的方法对吗?
甲同学先用刻度尺量得AB=CD,AD=BC,然后又用量角器量得其中一个内角∠DAB=90°,因此甲判定这个四边形ABCD是矩形。
有一个角是直角的平行四边形叫做矩形。
乙同学认为甲的方法太复杂,他只用量角器量得这个四边形的三个内角∠DAB 、∠ ABC、∠BCD都是90°,他就判定这个四边形ABCD是矩形。
有三个角是直角的四边形是矩形。
丙同学想了一下,他决定用与他们不同的方法来判断。他先用刻度尺量得AB=CD,AD=BC,然后又量得这个四边形的两条对角线AC=BD,他就判定这个 四边形是矩形。
对角线相等的平行四边形是矩形。
O
矩形的判定方法:
1、有一个角是直角的平行四边形是矩形。
2、对角线相等的平行四边形是矩形。
3、有三个角是直角的四边形是矩形。
对于1、2两种判定方法是在平行四边形的前提下来判断的,而3是直接在四边形的前提下判断的。
1、下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形; ( )
(3)对角线相等的四边形是矩形; ( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。
1、下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
2、满足下列条件( )的四边形是矩形.
(A)有三个角相等
(B)有一个角是直角
(C)对角线相等且互相垂直
(D)对角线相等且互相平分
3、已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形。
5.工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;
有一个角是直角的平行四边形是矩形
矩形判定方法1
有三个角是直角的四边形是矩形。
矩形判定方法2
对角线相等的平行四边形是矩形。
矩形判定方法3
习题19.2第2、3题。
矩 形
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形
即:
矩形是特殊的平行四边边形。它具有平行四边形
的一切性质。即
对边平行且相等.
对角相等,邻角互补.
对角线互相平分.
矩形的一般性质
边:
角:
对角线:
从边、角、对角线三个方面进行考虑,你能发现矩形有什么特有的性质吗?请以小组的形式讨论总结。
A
D
C
B
矩形的邻边垂直
A
B
C
D
矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明:∵矩形ABCD
∴AB∥CD
∴∠B+∠C=180 °
∵ ∠C=90 °
∴∠B=90°
∴∠A=∠B=∠C=∠D=90°
定理证明1
已知:四边形ABCD是矩形
求证:AC= BD
证明: ∵矩形ABCD
∴ ∠ABC = ∠DCB = 90°, AB = DC
又∵BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形的对角线相等
图中共有几个三角形?它们分别是什么三角形?
定理证明2
注:矩形的两条对角线把矩形分成了四个 等腰三角形
和四个直角三角形。
解题指导:矩形问题
直角三角形或等腰三角形
探究
等腰三角形:
△OAB △ OBC △OCD △OAD
直角三角形:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
O
OA,OB,OC,OD这4条线段有什么数量关系?
A
B
C
O
直角三角形斜边上的中线等于斜边的一半.
∵ 在Rt△ABC中, O是AC的中点,
∴BO= AC.
直角三角形的一个性质
几何语言:
(2)BO,AC分别是Rt△ABC的什么线段?
(3) BO与AC 有什么数量关系?为什么?
(4) 由此,你能得出什么结论?
(1)OA,OB,OC,OD这4条线段有什么数量关系?
矩形的性质
A
B
C
D
矩形的对边平行且相等.
对角线互相平分且相等
对称性
矩形是轴对称图形,
推论:
直角三角形斜边上的中线等于斜边的一半.
矩形问题
直角三角形或等腰三角形
(1)矩形具有而平行四边形不具有的性质( )
A.内角和是360度 B.对角相等
C.对边平行且相等 D.对角线相等
(2)下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线垂直
D
D
(3)四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
(4)在Rt△ABC中, 两条直角边分别是6和8.则斜边上的
中线长为 。
5
A
O
B
C
(3)
(4)
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长?
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4
∴ AC=BD=2OA=8
解:∵ 矩形ABCD
方法小结: 如果矩形两对角线的夹角是60°
或120°, 则其中必有等边三角形.
∴ AC与BD相等且互相平分
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
O
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
又∵ 矩形ABCD
法一:
∴ AC与BD相等且互相平分
O
∴ OA=OB
∴ ∠CAB=∠1
证明:∵ AE∥BD
∴ ∠EAB=∠1
∴ ∠EAB=∠CBA
1
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
证明∵ 矩形ABCD
法二:
∴ AD∥EB ,
O
又∵ AE∥BD
∴ 四边形AEBD是平行四边形
∴ ∠EAB=∠CBA
∴ AE=BD
又∵ ∠ABC=90°
∴ AE=AC
(等腰三角形的三线合一)
AC=BD
例2:在矩形ABCD中,AE∥BD,且交CB的延长线于点E,求证:∠EAB=∠CAB
证明∵ 矩形ABCD
法三:
∴ AD∥EB ,
O
又∵ AE∥BD
∴ 四边形AEBD是平行四边形
∴ △EAB≌△ CBA(SAS)
∴ AD=EB
又∵ ∠ABC=90°,AB=AB
∴ EB=BC
∴ ∠EAB=∠CBA
AD=BC
(1)知识结构图
(2)矩形不同于平行四边形的两条性质和推论
(3)解题指导:矩形问题
直角三角形或等腰三角形
(6)在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求矩形的周长及对角线的长
A
D
C
B
E
5
3
(4)在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AB= , AC=
B
C
D
E
A
O
4
2
1
1
(5)如图,在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求矩形的周长及对角线长。
5
3
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长?
变式:如图,矩形ABCD的两条对角线相交于点O,AC=8,求AB的长?
请你补充一个条件,使得问题可以解决。
(1)矩形具有而平行四边形不具有的性质( )
A.内角和是360度 B.对角相等
C.对边平行且相等 D.对角线相等
(2)下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线垂直
D
D
(3)已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 ( )
A.50° B.60° C.70° D.80°
D
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
矩形的特殊性质
有两组对边分别平行的四边形.
对边相等
邻边不相等
对角相等
邻角不相等
对边相等
邻边相等
对角相等
邻角相等
四条边都相等
四个角都相等
19.2特殊的平行四边形
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形
即:
生活中的矩形
矩形有什么性质?
有平行四边形的所有性质
还有其它特殊的性质
矩形的对边平行且相等.
矩形的对角相等.
矩形的对角线互相平分.
矩形的一般性质(即平行四边形所有性质)
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
矩形的特殊性质
矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
已知:四边形ABCD是矩形
求证:AC = BD
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形的对角线相等
矩形的性质
矩形的对边平行且相等.
对称性
矩形是轴对称图形,
也是中心对称图形.
A
B
C
O
直角三角形斜边上的中线等于斜边的一半.
在Rt△ABC中, BO是斜边AC上的中线,
则BO= AC.
直角三角形的一个性质
即:
D
证明: 延长BO至D,使OD=BO
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴AC=BD
在矩形ABCD中,找出相等的线段与相等的角.
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC
∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形:
△OAB △ OBC △OCD △OAD
直角三角形:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
在矩形ABCD中,找出所有等腰、直角、全等三角形.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长。
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
∴ OA=OB。
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长
AC=BD = 2OA=2×4=8(cm).
矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm。求AD的长及点A到BD的距离AE的长。
解:设AD=xcm,则对角线长(x+4)cm,在
Rt△ABD中,由勾股定理:
AD2+AB2=BD2 ∴
解得x=6。则 AD=6cm。
∵AE×DB= AD×AB
解得 AE= 4.8cm.
“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×DB= AD×AB
已知:矩形ABCD中,E是BC上一点,
DF⊥AE于F,若AE=BC.
求证:CE=EF。
脸蛋方方是矩形,例如黑板和窗门.
对角线段皆相等,相互交叉且平分.
内有直角三角形,斜边中线半斜边.
若要牢记其定义,直角平行四边形.
矩形之歌
矩形的定义:有一个角是直角的平行四边形.
矩形的性质:
具有平行四边形的一切特征.
四个角都是直角.
对角线相等且平分.
直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
1. 填空:
(1)矩形的定义中有两个条件:一是__________ ,
二是____________________ .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为____、____ 、 ____ 、 ____ 。
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为______ cm, ____ cm, ______ cm,____ cm。
有一个角是直角
平行四边形
60°
60°
120°
120°
5
5
2.下列说法错误的是( )
A. 矩形的对角线互相平分。
B. 矩形的对角线相等。
C. 有一个角是直角的四边形是矩形。
D. 有一个角是直角的平行四边形叫做矩形。
3. 矩形的对角线把矩形分成的三角形中全等三角形一共有( )
A. 2对 B. 4对 C. 6对 D. 8对
C
B
4. 工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是_________
______________
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边
框,当直角尺的两条直角边与窗框无缝隙时(如图4)
说明窗框合格,这时窗框是____,根据的数学道理
是_______________________
平行四边形
两组对边分别相等的
矩形
有一个角是直角的平行四边形是矩形
四边形是平行四边形
5. 用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
A. 48cm,12cm B. 48cm,16cm;
C. 44cm,16cm D. 45cm,15cm.
D
6. 四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
10. 小明想要做一个矩形像框,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?
1、理解并掌握矩形的判定方法。
2、能应用矩形定义、判定等知识,解决简单的证明题和计算题。
1.什么叫做平行四边形?什么叫做矩形?
2.矩形有哪些性质?
3.矩形与平行四边形有什么共同之处?有什么不同之处?
甲、乙、丙、丁四位同学到木工厂参观时,一木工师傅要他们利用自己所学的几何知识帮助检测一个窗框ABCD是不是矩形,他们各自做了检测。你认为他们的方法对吗?
甲同学先用刻度尺量得AB=CD,AD=BC,然后又用量角器量得其中一个内角∠DAB=90°,因此甲判定这个四边形ABCD是矩形。
有一个角是直角的平行四边形叫做矩形。
乙同学认为甲的方法太复杂,他只用量角器量得这个四边形的三个内角∠DAB 、∠ ABC、∠BCD都是90°,他就判定这个四边形ABCD是矩形。
有三个角是直角的四边形是矩形。
丙同学想了一下,他决定用与他们不同的方法来判断。他先用刻度尺量得AB=CD,AD=BC,然后又量得这个四边形的两条对角线AC=BD,他就判定这个 四边形是矩形。
对角线相等的平行四边形是矩形。
O
矩形的判定方法:
1、有一个角是直角的平行四边形是矩形。
2、对角线相等的平行四边形是矩形。
3、有三个角是直角的四边形是矩形。
对于1、2两种判定方法是在平行四边形的前提下来判断的,而3是直接在四边形的前提下判断的。
1、下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形; ( )
(3)对角线相等的四边形是矩形; ( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。
1、下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
2、满足下列条件( )的四边形是矩形.
(A)有三个角相等
(B)有一个角是直角
(C)对角线相等且互相垂直
(D)对角线相等且互相平分
3、已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形。
5.工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;
有一个角是直角的平行四边形是矩形
矩形判定方法1
有三个角是直角的四边形是矩形。
矩形判定方法2
对角线相等的平行四边形是矩形。
矩形判定方法3
习题19.2第2、3题。
