北师大数学九上 第四章 第34课时 相似三角形判定定理的证明 课件
文档属性
| 名称 | 北师大数学九上 第四章 第34课时 相似三角形判定定理的证明 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 686.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 10:01:59 | ||
图片预览



文档简介
课件9张PPT。 第四单元 图形的相似第34课时 相似三角形判定定理的证明北师大版 九年级上册考点 1 相似三角形的判定
1.如图所示,在矩形 ABCD 中,E 在 AD 上,EF⊥BE,EF 交 CD 于 F,
连接 BF,则图中与△ABE 一定相似的三角形是( )
A.△EFB B.△DEF C.△CFB D.△EFB 和△DEF
2.如果一个直角三角形的两条边长分别是 6 和 8,另一个与它相似的直角
三角形的边长分别是 3,4 及 x,那么 x 的值( )
A.只有 1 个 B.可以有 2 个 C.可以有 3 个 D.有无数个
针对训练·各个击破BB考点 1 相似三角形的判定
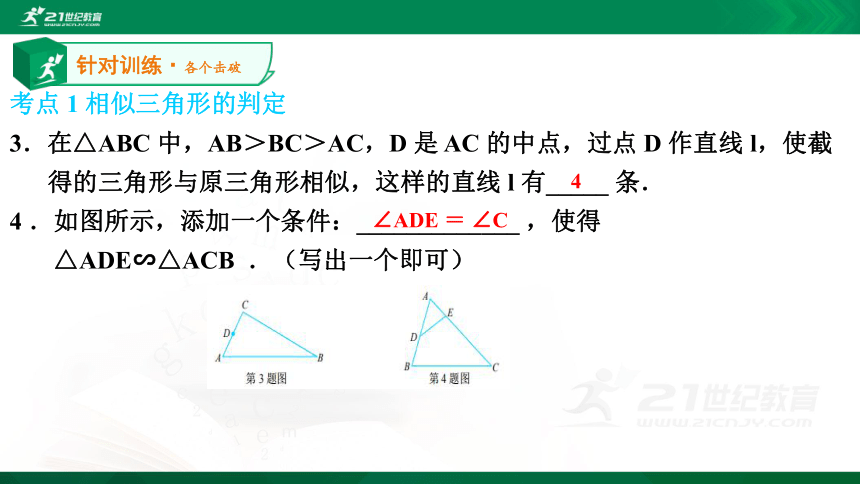
3.在△ABC 中,AB>BC>AC,D 是 AC 的中点,过点 D 作直线 l,使截
得的三角形与原三角形相似,这样的直线 l 有_____ 条.
4 .如图所示,添加一个条件:_____________ ,使得
△ADE∽△ACB .(写出一个即可)
针对训练·各个击破4∠ADE = ∠C考点 2 利用相似三角形解决相关问题
5.如图所示,在平行四边形 ABCD 中,点 E 在 AD 上,连接 CE 并延长,与
BA 的延长线交于点 F,若 AE=2ED,CD=3 cm, 则 AF 的长为( )
A.5 cm B.6 cm C.7 cm D.8 cm
6.如图所示,点 D,E 分别在 AB,AC 上,且∠ABC=∠AED.若 DE=4
,AE=5,BC=8,则 AB 的长为_______ .
针对训练·各个击破B10考点 2 利用相似三角形解决相关问题
7.如图所示,在△ABC 中,∠C=90°,BC=6,D,E 分别在 AB,AC 上
,将△ABC 沿 DE 折叠,使点 A 落在点 A′处,若 A′为 CE 的中点,则
折痕DE 的长为 ___ .针对训练·各个击破28.如图所示,AD 是△ABC 的中线,E 是 AD 上一点,且 CD2=DE·DA.
求证:∠BED=∠ABD.
【答案】∵AD 是△ABC 的中线,∴BD=CD,
而 CD2=DE·DA, ∴BD2=DE·DA.
可得
又∵∠BDE=∠ADB,
∴△BDE∽△ADB,
∴∠BED=∠ABD.
巩固提升·融会贯通9.已知:如图所示,△ABC 是等边三角形,点 D,E 分别在 CB,AC 的
延长线上,∠ADE=60°.求证:△ABD∽△DCE.
【答案】∵∠ABC=∠ACB=60°,
∴∠ABD=∠ECD=120°.
又∠ADB+∠DAB=∠ABC=60°, ∠ADB+∠EDC=60°,
∴∠DAB=∠EDC.
∴△ABD∽△DCE.
巩固提升·融会贯通10.在△ABC 中,AB=10 cm,BC=20 cm,点 P 从 A 开始沿 AB 边向 B
点以 2 cm/s 的速度移动,点 Q 从点 B 开始沿 BC 边向 C 点以 4 cm/s 的
速度移动,如果 P,Q 分别从 A,B 同时出发,经过几秒钟△PBQ 与
△ABC相似?
【答案】设经过 t 秒钟△PBQ 与△ABC 相似,
则有 AP=2t,BQ=4t,BP=10-2t.
当△PBQ∽△ABC 时,有 ,
当△QBP∽△ABC 时, .
∴经过 1 s 或 2.5 s,△PBQ 与△ABC 相似.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.如图所示,在矩形 ABCD 中,E 在 AD 上,EF⊥BE,EF 交 CD 于 F,
连接 BF,则图中与△ABE 一定相似的三角形是( )
A.△EFB B.△DEF C.△CFB D.△EFB 和△DEF
2.如果一个直角三角形的两条边长分别是 6 和 8,另一个与它相似的直角
三角形的边长分别是 3,4 及 x,那么 x 的值( )
A.只有 1 个 B.可以有 2 个 C.可以有 3 个 D.有无数个
针对训练·各个击破BB考点 1 相似三角形的判定
3.在△ABC 中,AB>BC>AC,D 是 AC 的中点,过点 D 作直线 l,使截
得的三角形与原三角形相似,这样的直线 l 有_____ 条.
4 .如图所示,添加一个条件:_____________ ,使得
△ADE∽△ACB .(写出一个即可)
针对训练·各个击破4∠ADE = ∠C考点 2 利用相似三角形解决相关问题
5.如图所示,在平行四边形 ABCD 中,点 E 在 AD 上,连接 CE 并延长,与
BA 的延长线交于点 F,若 AE=2ED,CD=3 cm, 则 AF 的长为( )
A.5 cm B.6 cm C.7 cm D.8 cm
6.如图所示,点 D,E 分别在 AB,AC 上,且∠ABC=∠AED.若 DE=4
,AE=5,BC=8,则 AB 的长为_______ .
针对训练·各个击破B10考点 2 利用相似三角形解决相关问题
7.如图所示,在△ABC 中,∠C=90°,BC=6,D,E 分别在 AB,AC 上
,将△ABC 沿 DE 折叠,使点 A 落在点 A′处,若 A′为 CE 的中点,则
折痕DE 的长为 ___ .针对训练·各个击破28.如图所示,AD 是△ABC 的中线,E 是 AD 上一点,且 CD2=DE·DA.
求证:∠BED=∠ABD.
【答案】∵AD 是△ABC 的中线,∴BD=CD,
而 CD2=DE·DA, ∴BD2=DE·DA.
可得
又∵∠BDE=∠ADB,
∴△BDE∽△ADB,
∴∠BED=∠ABD.
巩固提升·融会贯通9.已知:如图所示,△ABC 是等边三角形,点 D,E 分别在 CB,AC 的
延长线上,∠ADE=60°.求证:△ABD∽△DCE.
【答案】∵∠ABC=∠ACB=60°,
∴∠ABD=∠ECD=120°.
又∠ADB+∠DAB=∠ABC=60°, ∠ADB+∠EDC=60°,
∴∠DAB=∠EDC.
∴△ABD∽△DCE.
巩固提升·融会贯通10.在△ABC 中,AB=10 cm,BC=20 cm,点 P 从 A 开始沿 AB 边向 B
点以 2 cm/s 的速度移动,点 Q 从点 B 开始沿 BC 边向 C 点以 4 cm/s 的
速度移动,如果 P,Q 分别从 A,B 同时出发,经过几秒钟△PBQ 与
△ABC相似?
【答案】设经过 t 秒钟△PBQ 与△ABC 相似,
则有 AP=2t,BQ=4t,BP=10-2t.
当△PBQ∽△ABC 时,有 ,
当△QBP∽△ABC 时, .
∴经过 1 s 或 2.5 s,△PBQ 与△ABC 相似.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
