北师大数学九上 第四章 第37课时 相似三角形的性质(2) 课件
文档属性
| 名称 | 北师大数学九上 第四章 第37课时 相似三角形的性质(2) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 680.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 10:08:09 | ||
图片预览


文档简介
课件10张PPT。 第四单元 图形的相似第37课时 相似三角形的性质(2)北师大版 九年级上册考点 1 相似多边形的周长、面积的关系
1.若△ABC∽△A′B′C′,且相似比为 1︰2,则△ABC 与△A′B′C′的面积比
为( )
A.1︰2 B.2︰1 C.1︰4 D.4︰1
2.若两个相似三角形的面积比是 1∶2,则它们的周长比是( )
A.1︰2 B.1︰4 C.1︰ 2 D.2︰1
3.如图所示,在□ABCD 中,E 为 CD 上一点,连接 AE,BD,且 AE,BD
交于点 F,S△DEF︰S△ABF =4︰25 ,则 DE︰EC=( )
A.2︰5 B.2︰3 C.3︰5 D.3︰2
针对训练·各个击破CCB考点 1 相似多边形的周长、面积的关系
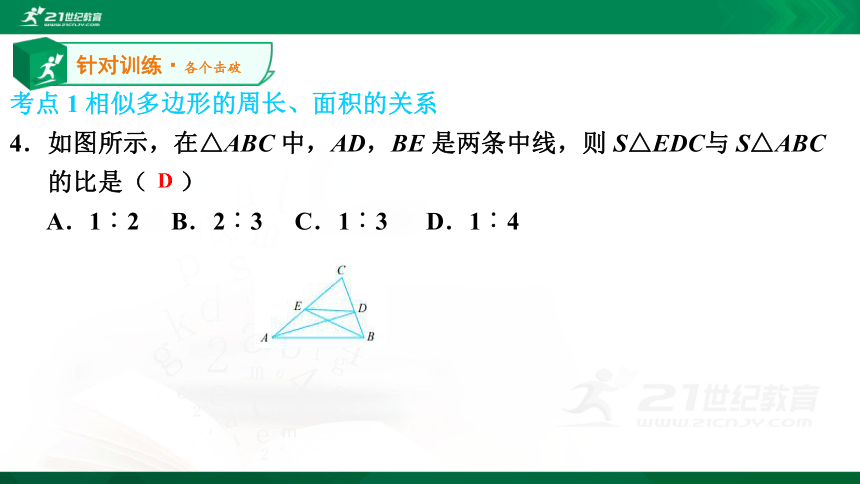
4.如图所示,在△ABC 中,AD,BE 是两条中线,则 S△EDC与 S△ABC
的比是( )
A.1︰2 B.2︰3 C.1︰3 D.1︰4
针对训练·各个击破D考点 2 相似比的应用
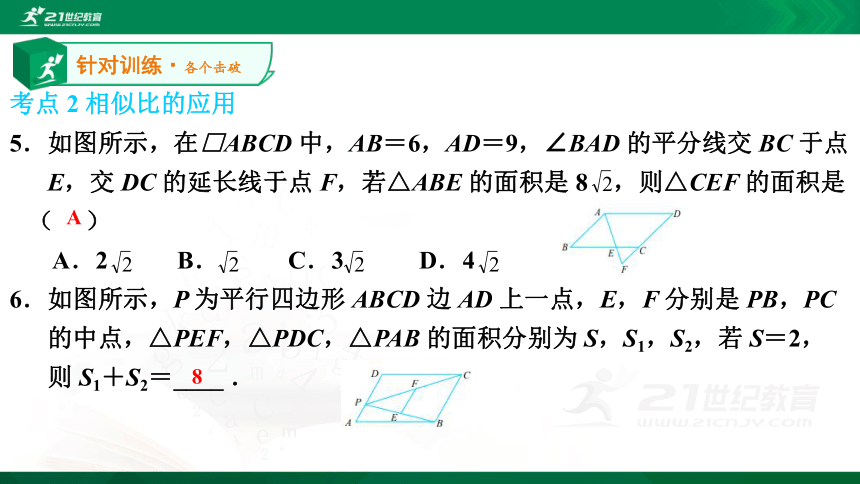
5.如图所示,在□ABCD 中,AB=6,AD=9,∠BAD 的平分线交 BC 于点
E,交 DC 的延长线于点 F,若△ABE 的面积是 8 ,则△CEF 的面积是
( )
A.2 B. C.3 D.4
6.如图所示,P 为平行四边形 ABCD 边 AD 上一点,E,F 分别是 PB,PC
的中点,△PEF,△PDC,△PAB 的面积分别为 S,S1,S2,若 S=2,
则 S1+S2=____ .
针对训练·各个击破A8考点 2 相似比的应用
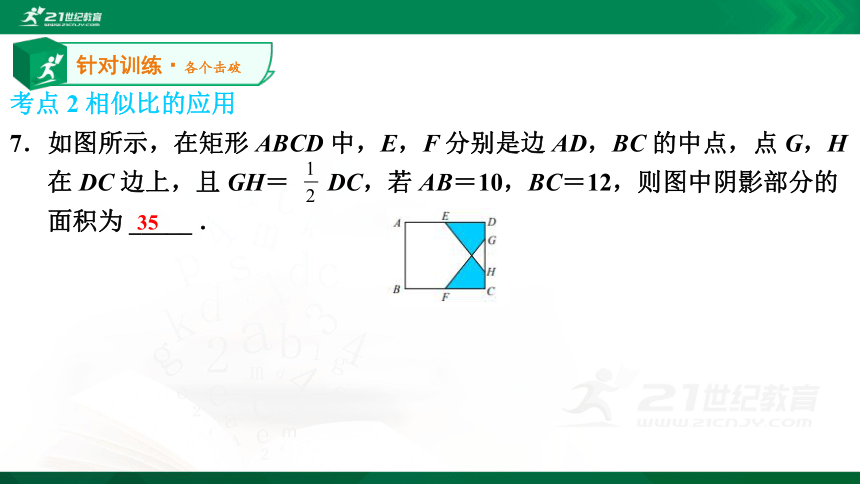
7.如图所示,在矩形 ABCD 中,E,F 分别是边 AD,BC 的中点,点 G,H
在 DC 边上,且 GH= DC,若 AB=10,BC=12,则图中阴影部分的
面积为 _____ . 针对训练·各个击破358.如图所示,在△ABC 中,EF∥BC,且 EF= BC=2 cm,△AEF 的周
长为 10 cm,试求梯形 BCFE 的周长.
【答案】∵EF∥BC,∴∠AEF=∠ABC,∠AFE=∠ACB,
∴△AEF∽△ABC.又∵EF= BC,
,即相似比为 .
∴△ABC 的周长=15(cm).
∴梯形 BCFE 的周长=△ABC 的周长-△AEF 周的长+2EF
=15-10+4=9(cm).
巩固提升·融会贯通9.如图所示,在梯形 ABCD 中,AB∥CD,AC 和 BD 相交于点 O,若
S△ODC︰S△AOB=1︰4,求 S△ODC︰S△AOB的值.
【答案】∵AB∥CD,∴∠CDO=∠ABO,∠DCO=∠BAO,
∴△OCD∽△OAB,
∴ OA=2OC.
又∵△ODC 和△ADO 同高,
即 S△ODC︰S△AOD的值为 .
巩固提升·融会贯通10.如图所示,在△ABC 中,BC >AC,点 D 在 BC 上,且 DC=AC,
∠ACB 的平分线 CF 交 AD 于 F,点 E 是 AB 的中点,连接 EF.
(1)求证:EF∥BC.
【答案】(1)∵DC=AC,CF 平分∠ACB,
∴CF 是△ACD 的中线,
∴点 F 是 AD 的中点.
又∵点 E 是 AB 的中点,
∴EF∥BD,即 EF∥BC.
巩固提升·融会贯通10.如图所示,在△ABC 中,BC >AC,点 D 在 BC 上,且 DC=AC,
∠ACB 的平分线 CF 交 AD 于 F,点 E 是 AB 的中点,连接 EF.
(2)若四边形 BDFE 的面积为 6,求△ABD 的面积.
【答案】(2)由(1)知,EF∥BD,∴△AEF∽△ABD ,
又∵AE= AB,S△AEF=S△ABD-S 四边形 BDFE=S△ABD-6,
∴ S△ABD=8,∴△ABD 的面积为 8.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.若△ABC∽△A′B′C′,且相似比为 1︰2,则△ABC 与△A′B′C′的面积比
为( )
A.1︰2 B.2︰1 C.1︰4 D.4︰1
2.若两个相似三角形的面积比是 1∶2,则它们的周长比是( )
A.1︰2 B.1︰4 C.1︰ 2 D.2︰1
3.如图所示,在□ABCD 中,E 为 CD 上一点,连接 AE,BD,且 AE,BD
交于点 F,S△DEF︰S△ABF =4︰25 ,则 DE︰EC=( )
A.2︰5 B.2︰3 C.3︰5 D.3︰2
针对训练·各个击破CCB考点 1 相似多边形的周长、面积的关系
4.如图所示,在△ABC 中,AD,BE 是两条中线,则 S△EDC与 S△ABC
的比是( )
A.1︰2 B.2︰3 C.1︰3 D.1︰4
针对训练·各个击破D考点 2 相似比的应用
5.如图所示,在□ABCD 中,AB=6,AD=9,∠BAD 的平分线交 BC 于点
E,交 DC 的延长线于点 F,若△ABE 的面积是 8 ,则△CEF 的面积是
( )
A.2 B. C.3 D.4
6.如图所示,P 为平行四边形 ABCD 边 AD 上一点,E,F 分别是 PB,PC
的中点,△PEF,△PDC,△PAB 的面积分别为 S,S1,S2,若 S=2,
则 S1+S2=____ .
针对训练·各个击破A8考点 2 相似比的应用
7.如图所示,在矩形 ABCD 中,E,F 分别是边 AD,BC 的中点,点 G,H
在 DC 边上,且 GH= DC,若 AB=10,BC=12,则图中阴影部分的
面积为 _____ . 针对训练·各个击破358.如图所示,在△ABC 中,EF∥BC,且 EF= BC=2 cm,△AEF 的周
长为 10 cm,试求梯形 BCFE 的周长.
【答案】∵EF∥BC,∴∠AEF=∠ABC,∠AFE=∠ACB,
∴△AEF∽△ABC.又∵EF= BC,
,即相似比为 .
∴△ABC 的周长=15(cm).
∴梯形 BCFE 的周长=△ABC 的周长-△AEF 周的长+2EF
=15-10+4=9(cm).
巩固提升·融会贯通9.如图所示,在梯形 ABCD 中,AB∥CD,AC 和 BD 相交于点 O,若
S△ODC︰S△AOB=1︰4,求 S△ODC︰S△AOB的值.
【答案】∵AB∥CD,∴∠CDO=∠ABO,∠DCO=∠BAO,
∴△OCD∽△OAB,
∴ OA=2OC.
又∵△ODC 和△ADO 同高,
即 S△ODC︰S△AOD的值为 .
巩固提升·融会贯通10.如图所示,在△ABC 中,BC >AC,点 D 在 BC 上,且 DC=AC,
∠ACB 的平分线 CF 交 AD 于 F,点 E 是 AB 的中点,连接 EF.
(1)求证:EF∥BC.
【答案】(1)∵DC=AC,CF 平分∠ACB,
∴CF 是△ACD 的中线,
∴点 F 是 AD 的中点.
又∵点 E 是 AB 的中点,
∴EF∥BD,即 EF∥BC.
巩固提升·融会贯通10.如图所示,在△ABC 中,BC >AC,点 D 在 BC 上,且 DC=AC,
∠ACB 的平分线 CF 交 AD 于 F,点 E 是 AB 的中点,连接 EF.
(2)若四边形 BDFE 的面积为 6,求△ABD 的面积.
【答案】(2)由(1)知,EF∥BD,∴△AEF∽△ABD ,
又∵AE= AB,S△AEF=S△ABD-S 四边形 BDFE=S△ABD-6,
∴ S△ABD=8,∴△ABD 的面积为 8.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
