北师大版八年级数学上第四章《一次函数》导学案(无答案)
文档属性
| 名称 | 北师大版八年级数学上第四章《一次函数》导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 00:00:00 | ||
图片预览



文档简介
北师大版八年级数学上第四章《一次函数》导学案
知识点:函数的概念
定义:在某一变化过程中,可以取不同数值的量,叫做变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
例1:求下列函数中自变量x的取值范围:
(1); (2).
例2:圆柱底面半径为5cm,则圆柱的体积V(cm3)与圆柱的高h(cm)之间的函数关系式为 ,它是 函数.
知识点:一次函数的概念
定义:一次函数:若两个变量x、y间的关系可以表示成 (k、b 为常数,k≠0)形式,则称y是x的一次函数(x是自变量,y是因变量).特别地,当b=0时,称y是x的____________.正比例函数是一次函数的特殊情况.
例1:有下列函数:①y=-x-2;②y=-;③y=-x2+(x +1)(x-2);④y=-2,
其中不是一次函数的是 .(填序号)
例2:要使y=(m-2)xn-1+n是关于x的一次函数,则m、n应满足______________.
例3:已知y=(k-1)是正比例函数,则k= .
【变式练习】
1、若函数y = (k+1)x+k2-1是正比例函数,则k的值为( )
A.0 B.1 C.±1 D.-1
2、若是正比例函数,则b的值是( )
A. 0 B. C. D.
3.下列关于x的函数中,是一次函数的是( )
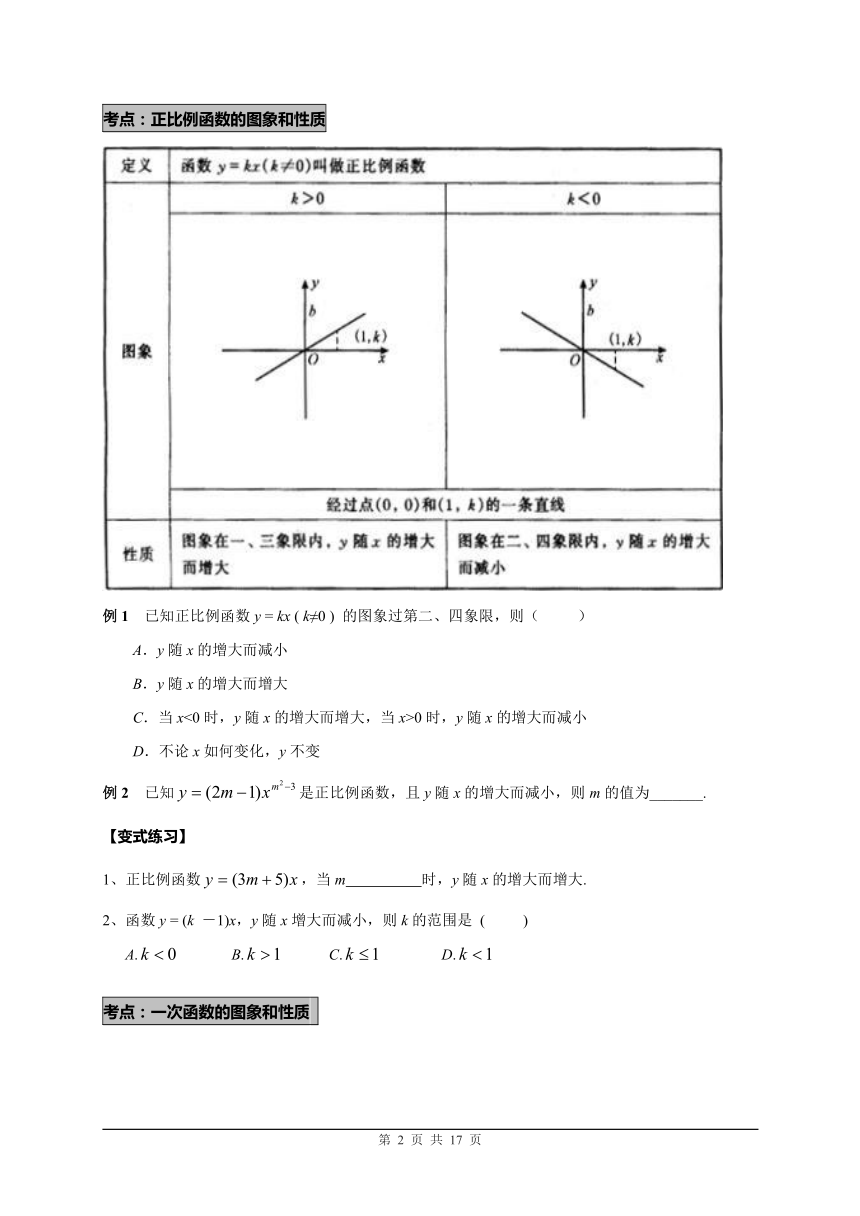
考点:正比例函数的图象和性质
例1 已知正比例函数y = kx ( k≠0 ) 的图象过第二、四象限,则( )
A.y随x的增大而减小
B.y随x的增大而增大
C.当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小
D.不论x如何变化,y不变
例2 已知是正比例函数,且y随x的增大而减小,则m的值为_______.
【变式练习】
1、正比例函数,当m 时,y随x的增大而增大.
2、函数y = (k -1)x,y随x增大而减小,则k的范围是 ( )
A. B. C. D.
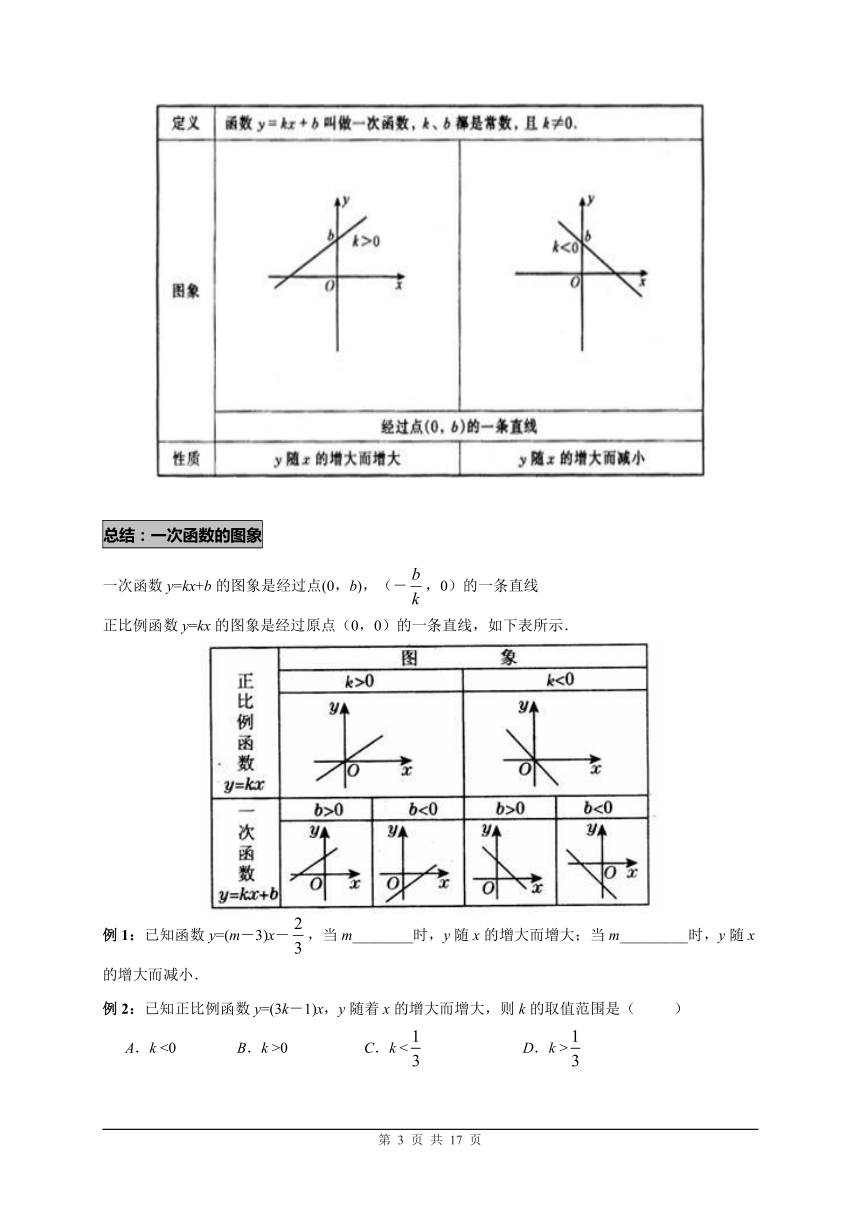
考点:一次函数的图象和性质
总结:一次函数的图象
一次函数y=kx+b的图象是经过点(0,b),(-,0)的一条直线
正比例函数y=kx的图象是经过原点(0,0)的一条直线,如下表所示.
例1:已知函数y=(m-3)x-,当m________时,y随x的增大而增大;当m_________时,y随x的增大而减小.
例2:已知正比例函数y=(3k-1)x,y随着x的增大而增大,则k的取值范围是( )
A.k <0 B.k >0 C.k < D.k >
例3:如图,表示一次函数与正比例函数(为常数,且)图象的是( )
【变式练习】
1、两个一次函数y1= mx+n,y2= nx+m,它们在同一坐标系中的图象可能是图中的( )
2、已知函数,当时,y的取值范围是( )
A. B. C. D.
3、若关于x的函数是一次函数,则m= ,n .
4、若m < 0,n > 0,则一次函数y= mx + n的图象不经过( )
A.第一象限 B. 第二象限 C.第三象限 D.第四象限
考点:直线的平移:
例1:在同一平面直角坐标系中画出下列函数的图象.
y=2x与y=2x+3
观察y=2x与y=2x+3两条直线,它们有什么样的位置关系?
请回答:两条直线与平行,那么____,____
直线的平移: 左“+”右“-”,上“+”下“-”
点的平移同样按照“左‘+’右‘-’,上‘+’下‘-’”.平移几个单位就加上或者减去几.
例2:直线y=-2x与直线y=-2x-4的位置关系是__________.
函数y=-2x-4图象可以由函数y=-2x的图象向______平移_____个单位得到.
【变式练习】
1、下列说法是否正确,为什么?
(1)直线y = 3x+1与y =-3x+1平行;
(2)直线与重合;
(3)直线y=-x-3与y=-x平行;
(4)直线与相交.
2、将直线y=3x向下平移5个单位,得到直线 ;将直线y=-x-5向上平移5个单位,得到直线 .
考点:用待定系数法确定一次函数表达式的一般步骤:一设,二代,三解,四代入:
(1)设一次函数表达式为y=kx+b;
(2)将已知点的坐标代入函数表达式,解方程(组);
(3)求出k与b的值;
(4)将k、b的值带入y=kx+b,得到函数表达式.
例如:已知一次函数的图象经过点(2,1)和(-1,-3)求此一次函数的关系式.
解:设一次函数的关系式为y=kx+b(k≠0),
由题意可知, 解 ∴此函数的关系式为y=.
例1:已知正比例函数的图象如下图如示,则正比例函数的解析式为多少?
例2:已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的关系式
例3:一次函数y=3x+b的图象与两坐标轴围成的三角形面积是24,求b.
例4. 若一次函数y=kx+b的图象经过(0,1)和(-1,3)两点,则此函数的解析式为_____________.
例5、若正比例函数y = kx的图象经过点(1,2),则此函数的解析式为_____________.
例6. 直线y=2x+8与x轴和y轴的交点的坐标分别是_______、_______.
例7、已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
【变式练习】
1. 油箱中存油20升,油从油箱中均匀流出,流速为0.2升/分钟,则油箱中剩余油量 Q(升)与流出时间t(分钟)的函数关系是( )
A.Q=0.2t B.Q=20-0.2t C.t=0.2Q D.t=20—0.2Q
2. 若正比例函数的图象经过(-l,5)那么这个函数的表达式为__________,y的值随x 的减小而____________
3. 若一次函数y=kx-3经过点(3,0),则k= ,该图象还经过点( 0, )和( ,-2)
4. 一某市市内出租车行程在 4km以内(含 4km)收起步费 8元,行驶超过4km时,每超过1 km,加收1.80元,当行程超出4km时收费y元与所行里程x(km)之间的函数关系式 .
5. 小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与卖瓜的千克数之间的关系如图l-6-3所示,那么小李赚了( )
A.32元 B.36元 C.38元 D.44元
6. 直线 y=x+4与 x轴交于 A,与y轴交于B, O为原点,则△AOB的面积为( )
A.12 B.24 C.6 D.10
7.一次函数的图象如图l-6-42所示,那么这个一次函数的表达式是( )
A.y=-2x+2 B.y=-2x-2 C.y= 2x+2 D.y=2x-2
考点:一次函数的应用
例1. 如果每盒圆珠笔有12支,售价6元,那么圆珠笔的售价y(元)与圆珠笔的支数x(支)之间的关系式是( )
A.y= x B.y=2x C.y=6x D.y=12x
例2. 幸福村办工厂,今年前五个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图l-6-43所示,则该工厂对这种产品来说( )
A.1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减小
B.l月至3月生产总量逐月增加,4、5两月生产总量与3月持平
C.l月至3月每月生产总量逐月增加,4、5两月均停止生产
D.l月至3月每月生产总量不变,4、5两月均停止生产
例3. 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图像信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同? 请说明理由;
(2)求返程中y与x之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
【变式练习】
1、一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走了一段路程,爸爸才开始出发.图l-6-44中两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t(分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( )
A.爸爸登山时,小军已走了50米
B.爸爸走了5分钟,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10分钟登山的速度比小军慢,10分钟后登山的速度比小军快
2. 某地区的电力资源丰富,并且得到了较好的开发. 该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费. 月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
⑴ 月用电量为100度时,应交电费 元;
⑵ 当x≥100时,求y与x之间的函数关系式;
⑶ 月用电量为260度时,应交电费多少元?
基础练习
1. 下列函数是一次函数的是 .
①y=2x;②y=3+4x;③y=0.5;④y=ax(a≠0的常数);⑤xy=3;⑥2x+3y-1=0;
2. 若函数y=(m-2)x+5是一次函数,则m满足的条件是____________.
3.已知y与x-1成正比例,且x=2时,y=7.
(1)写出y与x之间的函数关系:_________;(2)y与x之间是_________函数关系
4.已知一次函数y=kx+5的图象经过点(-1,2),则k=_______,图象不经过_______象限.
6.如果直线y=kx+b经过一、二、四象限,那么有( )
A.k>0,b>0 B.k>0,b<0 C.k < 0,b<0 D.k<0,b>0
7. 已知函数:①y=-x,②y=7-3x,③y=3x-1,④y=3x2,⑤y= ,⑥y= 中,正比例函数有( )
A.①⑤ B.①④ C.①③ D.③⑥
8.(1)当m= 时,y=是一次函数.
(2)我国是一个水资源缺乏的国家,大家要节约用水.据统计,拧不紧的水龙头每秒钟会滴下2 滴水,每滴水约0.05毫升.李丽同学在洗手时,没有把水龙头拧紧,当李丽同学离开x小时后水龙头滴了y毫升水.则y与x之间的函数关系式是 .
(4)设圆的面积为s,半径为R,那么下列说法正确的是( )
A.S是R的一次函数 B.S是R的正比例函数
C.S是的正比例函数 D.以上说法都不正确
9.已知一次函数y=(m+2)x+m -m-4的图象经过点(0,2),则m的值是(??? ? )
A.2?????? B.-2??????? C.-2或3????? D.3
10.直线y=-x+2与x轴的交点坐标是 ,与y轴的交点坐标是 .
直线y=-x-1与x轴的交点坐标是 ,与y轴的交点坐标是 .
直线y=4x-2与x轴的交点坐标是 ,与y轴的交点坐标是 .
直线y=与x轴的交点坐标是 ,与y轴的交点坐标是 .
12. 在下列四个函数中,的值随值的增大而减小的是( )
A. B. C. D.
13、直线和的位置关系是 ,直线可以看作是直线向 平移 个单位得到的.
14. 将直线y=-2x+3向下平移5个单位,得到直线 .
15. 直线y=kx-4平行于直线y=-2x,则直线的解析式为 ;
16.电话每台月租费28元,市区内电话(三分钟以内)每次0.20元,若某台电话每次通话均不超过3分钟,则每月应缴费y(元)与市内电话通话次数x之间的函数关系式是( )
A.y=28x+0.20 B.y=0.20x+28x C.y=0.20x+28 D.y=28-0.20x
17.某人购进一批苹果到集市上零售,已知卖出的苹果x(千克)与销售的金额y元的关系如下表:
x(千克) 1 2 3 4 5 …
y(元) 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5 …
(1)写出y与x的函数关系式:___________;
(2)该商贩要想使销售的金额达到250元,至少需要卖出多少千克的苹果?
18.如图2-4,某游客为爬上3千米的山顶看日出,先用1小时爬了2千米,休息0.5小时后,再用1小时爬上山顶,游客爬山所用时间t(小时)与山高h(千米)间的函数关系用图象表示是( )
19.一次函数的图象与y轴的交点坐标是_________,与x轴的交点坐标是_________.一般的,一次函数y=kx+b与y轴的交点坐标是__________,与x轴的交点坐标是__________.
20.依据给定的条件,求一次函数的解析式.
(1)已知一次函数的图象如图4-5所示,求此一次函数的解析式,并判断点(6,5)是否在此函数图象上.
图4-5
(2)已知一次函数y=2x+b的图象与y轴的交点到x轴的距离是4,求其函数解析式.
21.依据给定的条件,求一次函数解析式:y=ax+7经过一次函数y=4-3x和y=2x-1的交点.
22、已知函数轴交点的纵坐标为,且当x=1时,y=2,则此函数的解析式。
23. 已知y-1与成正比例,且x=2时,y=5,写出y与x之间的函数关系式。
24.如图3-4,居室窗户的高90cm,活动窗拉开的最大距离是80cm.如果活动窗拉开xcm时,窗户的通风面积是ycm2.
(1)试确定这个函数的解析式并指出自变量x的取值范围;
(2)画出这个函数的图象.
图3-4
25.某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据如下表:
砝码的质量(x克) 0 50 100 150 200 250 300 400 500
指针位置(y厘米) 2 3 4 5 6 7 7.5 7.5 7.5
(1)求出y与x的函数关系式;
(2)y关于x的函数图象是( )
图6-5
26.气温随着高度的增加而下降,下降的一般规律是从地面到高空11km处,每升高1km,气温下降6℃.高于11km时,气温几乎不再变化,设地面的气温为38℃,高空中xkm的气温为y℃.当0≤x≤11时,求y与x之间的关系式.
27.我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图6-6所示.
(1)观察图象,求出函数在不同范围内的解析式;
(2)说出自来水公司在这两个用水范围内的收费标准;
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
图6-6
提高练习
1.一次函数的图象过点A(5,3)且平行于直线y=3x-,则这个函数的解析式为________.
2. 一次函数与的图象如图,则下列结论:
①;②;③当时,中,正确的个数是( )
A.0 B.1 C.2 D.3
3.已知一次函数图象经过点(2,3),且与y轴交点的纵坐标为4,则这个函数的表达式是____.
4、一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点 B(3,3),则光线从A点到B点经过的路线长是 ;直线BC的解析式为 .
5. 若 ab>0,bc<0,则直线y=-x-不通过( )
A.第一象限 B.第一象限 C.第三象限 D.第四象限
6. 已知一次函数y= x+m和y= -x+n的图象都经过点A(-2,0)且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
7.已知函数的图象如图,则的图象可能是( )
9. 如图(1),在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至
点D停止.设点P运动的路程为,△ABP的面积为y,如果y关于x的函
数图象如图(2)所示,则△BCD的面积是( )
A.3 B.4 C.5 D.6
10. 如图,在中学生耐力测试比赛中,甲、乙两学生测试的路程s (米)与时间t (秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
A.乙比甲先到终点
B.乙测试的速度随时间增加而增大
C.比赛到29.4秒时,两人出发后第一次相遇
D.比赛全程甲测试速度始终比乙测试速度快
11. 小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达
点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.
下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保
持和去上班时一致,那么他从单位到家门口需要的时间是( )
A.12分钟 B.15分钟 C.25分钟 D.27分钟
12、如右图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是( )
13、如图1,在矩形中,动点从点出发,沿→→→方向运动至点处停止.设点运动的路程为,的面积为,如果关于的函数图象如图2所示,则当时,点应运动到( )
A.处 B.处 C.处 D.处
14. 求函数与x轴、y轴的交点坐标,并求这条直线与两坐标轴围成的三角形的面积.
15、已知两直线y1=2x-3,y2=6-x(1)在同一坐标系中作出它们的图象.(2)求它们的交点A的坐标.(3)根据图象指出x为何值时,y1>y2;x为何值时,y1<y2.(4)求这两条直线与x轴所围成的△ABC的面积.
16、已知一次函数y=kx+b的图像经过点A(0,2)和点B(-a,3)且点B在正比例函数y=-3x的图像上.(1) 求a的值;(2) 求一次函数的解析式.
17. 如图,直线l1、l2相交于点A,l1与x轴的交点坐标为(-1,0),l2与y轴的交点坐标为(0,-2),结合图象解答下列问题:
(1)求出直线l2表示的一次函数表达式;
(2)当x为何值时,l1、l2表示的两个一次函数的函数值都大于0?
18. 已知直线 y=x+2与直线 y= x+2交于 C点,直线y= -x+2与x轴交点为A,直线y= x+2与x轴交点为B.求△ABC的面积.
19.有一长方形AOBC纸片放在如图3-3所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出x=-5时,函数y的值;
(3)求出y=-5时,自变量x的值;
(4)画这个函数的图象;
(5)根据图象回答,当x从2减小到-3时,y的值是如何变化的?
图3-3
20.如图5-1,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的数据:
指距d(cm) 20 22
身高h(cm) 160 178
(1)求出h与d之间的函数关系式(不要求写出自变量d的取值范围);
(2)某人身高为196cm,一般情况下他的指距应是多少?
图5-1
21.某造纸厂污水处理的剩余污水随着时间的增加而减少,剩余污水量V(万米3)与污水处理时间t(天)的关系如图5-2所示,
(1)由图象求出剩余污水量V(万米3)与污水处理时间t(天)之间的函数解析式;
(2)污水处理连续10天,剩余污水还有多少万立方米?
(3)按照图中的规律,若想将全部污水处理干净,需要连续处理污水多少天?
(4)平均一天可处理污水多少万立方米?
图5-2
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
向左(右)平移p个单位
向上(下)平移p个单位
x
y
O
3
第2题图
第7题图
图(1)
2
O
5
x
A
B
C
P
D
图(2)
第9题图
1
2
3
4
1
2
y
s
O
1
2
3
4
1
2
y
s
O
s
1
2
3
4
1
2
y
s
O
1
2
3
4
1
2
y
O
A.
B.
C.
D.
Q
P
R
M
N
(图1)
(图2)
4
9
y
x
O
第 16 页 共 17 页
知识点:函数的概念
定义:在某一变化过程中,可以取不同数值的量,叫做变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
例1:求下列函数中自变量x的取值范围:
(1); (2).
例2:圆柱底面半径为5cm,则圆柱的体积V(cm3)与圆柱的高h(cm)之间的函数关系式为 ,它是 函数.
知识点:一次函数的概念
定义:一次函数:若两个变量x、y间的关系可以表示成 (k、b 为常数,k≠0)形式,则称y是x的一次函数(x是自变量,y是因变量).特别地,当b=0时,称y是x的____________.正比例函数是一次函数的特殊情况.
例1:有下列函数:①y=-x-2;②y=-;③y=-x2+(x +1)(x-2);④y=-2,
其中不是一次函数的是 .(填序号)
例2:要使y=(m-2)xn-1+n是关于x的一次函数,则m、n应满足______________.
例3:已知y=(k-1)是正比例函数,则k= .
【变式练习】
1、若函数y = (k+1)x+k2-1是正比例函数,则k的值为( )
A.0 B.1 C.±1 D.-1
2、若是正比例函数,则b的值是( )
A. 0 B. C. D.
3.下列关于x的函数中,是一次函数的是( )
考点:正比例函数的图象和性质
例1 已知正比例函数y = kx ( k≠0 ) 的图象过第二、四象限,则( )
A.y随x的增大而减小
B.y随x的增大而增大
C.当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小
D.不论x如何变化,y不变
例2 已知是正比例函数,且y随x的增大而减小,则m的值为_______.
【变式练习】
1、正比例函数,当m 时,y随x的增大而增大.
2、函数y = (k -1)x,y随x增大而减小,则k的范围是 ( )
A. B. C. D.
考点:一次函数的图象和性质
总结:一次函数的图象
一次函数y=kx+b的图象是经过点(0,b),(-,0)的一条直线
正比例函数y=kx的图象是经过原点(0,0)的一条直线,如下表所示.
例1:已知函数y=(m-3)x-,当m________时,y随x的增大而增大;当m_________时,y随x的增大而减小.
例2:已知正比例函数y=(3k-1)x,y随着x的增大而增大,则k的取值范围是( )
A.k <0 B.k >0 C.k < D.k >
例3:如图,表示一次函数与正比例函数(为常数,且)图象的是( )
【变式练习】
1、两个一次函数y1= mx+n,y2= nx+m,它们在同一坐标系中的图象可能是图中的( )
2、已知函数,当时,y的取值范围是( )
A. B. C. D.
3、若关于x的函数是一次函数,则m= ,n .
4、若m < 0,n > 0,则一次函数y= mx + n的图象不经过( )
A.第一象限 B. 第二象限 C.第三象限 D.第四象限
考点:直线的平移:
例1:在同一平面直角坐标系中画出下列函数的图象.
y=2x与y=2x+3
观察y=2x与y=2x+3两条直线,它们有什么样的位置关系?
请回答:两条直线与平行,那么____,____
直线的平移: 左“+”右“-”,上“+”下“-”
点的平移同样按照“左‘+’右‘-’,上‘+’下‘-’”.平移几个单位就加上或者减去几.
例2:直线y=-2x与直线y=-2x-4的位置关系是__________.
函数y=-2x-4图象可以由函数y=-2x的图象向______平移_____个单位得到.
【变式练习】
1、下列说法是否正确,为什么?
(1)直线y = 3x+1与y =-3x+1平行;
(2)直线与重合;
(3)直线y=-x-3与y=-x平行;
(4)直线与相交.
2、将直线y=3x向下平移5个单位,得到直线 ;将直线y=-x-5向上平移5个单位,得到直线 .
考点:用待定系数法确定一次函数表达式的一般步骤:一设,二代,三解,四代入:
(1)设一次函数表达式为y=kx+b;
(2)将已知点的坐标代入函数表达式,解方程(组);
(3)求出k与b的值;
(4)将k、b的值带入y=kx+b,得到函数表达式.
例如:已知一次函数的图象经过点(2,1)和(-1,-3)求此一次函数的关系式.
解:设一次函数的关系式为y=kx+b(k≠0),
由题意可知, 解 ∴此函数的关系式为y=.
例1:已知正比例函数的图象如下图如示,则正比例函数的解析式为多少?
例2:已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的关系式
例3:一次函数y=3x+b的图象与两坐标轴围成的三角形面积是24,求b.
例4. 若一次函数y=kx+b的图象经过(0,1)和(-1,3)两点,则此函数的解析式为_____________.
例5、若正比例函数y = kx的图象经过点(1,2),则此函数的解析式为_____________.
例6. 直线y=2x+8与x轴和y轴的交点的坐标分别是_______、_______.
例7、已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
【变式练习】
1. 油箱中存油20升,油从油箱中均匀流出,流速为0.2升/分钟,则油箱中剩余油量 Q(升)与流出时间t(分钟)的函数关系是( )
A.Q=0.2t B.Q=20-0.2t C.t=0.2Q D.t=20—0.2Q
2. 若正比例函数的图象经过(-l,5)那么这个函数的表达式为__________,y的值随x 的减小而____________
3. 若一次函数y=kx-3经过点(3,0),则k= ,该图象还经过点( 0, )和( ,-2)
4. 一某市市内出租车行程在 4km以内(含 4km)收起步费 8元,行驶超过4km时,每超过1 km,加收1.80元,当行程超出4km时收费y元与所行里程x(km)之间的函数关系式 .
5. 小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与卖瓜的千克数之间的关系如图l-6-3所示,那么小李赚了( )
A.32元 B.36元 C.38元 D.44元
6. 直线 y=x+4与 x轴交于 A,与y轴交于B, O为原点,则△AOB的面积为( )
A.12 B.24 C.6 D.10
7.一次函数的图象如图l-6-42所示,那么这个一次函数的表达式是( )
A.y=-2x+2 B.y=-2x-2 C.y= 2x+2 D.y=2x-2
考点:一次函数的应用
例1. 如果每盒圆珠笔有12支,售价6元,那么圆珠笔的售价y(元)与圆珠笔的支数x(支)之间的关系式是( )
A.y= x B.y=2x C.y=6x D.y=12x
例2. 幸福村办工厂,今年前五个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图l-6-43所示,则该工厂对这种产品来说( )
A.1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减小
B.l月至3月生产总量逐月增加,4、5两月生产总量与3月持平
C.l月至3月每月生产总量逐月增加,4、5两月均停止生产
D.l月至3月每月生产总量不变,4、5两月均停止生产
例3. 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图像信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同? 请说明理由;
(2)求返程中y与x之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
【变式练习】
1、一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走了一段路程,爸爸才开始出发.图l-6-44中两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t(分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( )
A.爸爸登山时,小军已走了50米
B.爸爸走了5分钟,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10分钟登山的速度比小军慢,10分钟后登山的速度比小军快
2. 某地区的电力资源丰富,并且得到了较好的开发. 该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费. 月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
⑴ 月用电量为100度时,应交电费 元;
⑵ 当x≥100时,求y与x之间的函数关系式;
⑶ 月用电量为260度时,应交电费多少元?
基础练习
1. 下列函数是一次函数的是 .
①y=2x;②y=3+4x;③y=0.5;④y=ax(a≠0的常数);⑤xy=3;⑥2x+3y-1=0;
2. 若函数y=(m-2)x+5是一次函数,则m满足的条件是____________.
3.已知y与x-1成正比例,且x=2时,y=7.
(1)写出y与x之间的函数关系:_________;(2)y与x之间是_________函数关系
4.已知一次函数y=kx+5的图象经过点(-1,2),则k=_______,图象不经过_______象限.
6.如果直线y=kx+b经过一、二、四象限,那么有( )
A.k>0,b>0 B.k>0,b<0 C.k < 0,b<0 D.k<0,b>0
7. 已知函数:①y=-x,②y=7-3x,③y=3x-1,④y=3x2,⑤y= ,⑥y= 中,正比例函数有( )
A.①⑤ B.①④ C.①③ D.③⑥
8.(1)当m= 时,y=是一次函数.
(2)我国是一个水资源缺乏的国家,大家要节约用水.据统计,拧不紧的水龙头每秒钟会滴下2 滴水,每滴水约0.05毫升.李丽同学在洗手时,没有把水龙头拧紧,当李丽同学离开x小时后水龙头滴了y毫升水.则y与x之间的函数关系式是 .
(4)设圆的面积为s,半径为R,那么下列说法正确的是( )
A.S是R的一次函数 B.S是R的正比例函数
C.S是的正比例函数 D.以上说法都不正确
9.已知一次函数y=(m+2)x+m -m-4的图象经过点(0,2),则m的值是(??? ? )
A.2?????? B.-2??????? C.-2或3????? D.3
10.直线y=-x+2与x轴的交点坐标是 ,与y轴的交点坐标是 .
直线y=-x-1与x轴的交点坐标是 ,与y轴的交点坐标是 .
直线y=4x-2与x轴的交点坐标是 ,与y轴的交点坐标是 .
直线y=与x轴的交点坐标是 ,与y轴的交点坐标是 .
12. 在下列四个函数中,的值随值的增大而减小的是( )
A. B. C. D.
13、直线和的位置关系是 ,直线可以看作是直线向 平移 个单位得到的.
14. 将直线y=-2x+3向下平移5个单位,得到直线 .
15. 直线y=kx-4平行于直线y=-2x,则直线的解析式为 ;
16.电话每台月租费28元,市区内电话(三分钟以内)每次0.20元,若某台电话每次通话均不超过3分钟,则每月应缴费y(元)与市内电话通话次数x之间的函数关系式是( )
A.y=28x+0.20 B.y=0.20x+28x C.y=0.20x+28 D.y=28-0.20x
17.某人购进一批苹果到集市上零售,已知卖出的苹果x(千克)与销售的金额y元的关系如下表:
x(千克) 1 2 3 4 5 …
y(元) 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5 …
(1)写出y与x的函数关系式:___________;
(2)该商贩要想使销售的金额达到250元,至少需要卖出多少千克的苹果?
18.如图2-4,某游客为爬上3千米的山顶看日出,先用1小时爬了2千米,休息0.5小时后,再用1小时爬上山顶,游客爬山所用时间t(小时)与山高h(千米)间的函数关系用图象表示是( )
19.一次函数的图象与y轴的交点坐标是_________,与x轴的交点坐标是_________.一般的,一次函数y=kx+b与y轴的交点坐标是__________,与x轴的交点坐标是__________.
20.依据给定的条件,求一次函数的解析式.
(1)已知一次函数的图象如图4-5所示,求此一次函数的解析式,并判断点(6,5)是否在此函数图象上.
图4-5
(2)已知一次函数y=2x+b的图象与y轴的交点到x轴的距离是4,求其函数解析式.
21.依据给定的条件,求一次函数解析式:y=ax+7经过一次函数y=4-3x和y=2x-1的交点.
22、已知函数轴交点的纵坐标为,且当x=1时,y=2,则此函数的解析式。
23. 已知y-1与成正比例,且x=2时,y=5,写出y与x之间的函数关系式。
24.如图3-4,居室窗户的高90cm,活动窗拉开的最大距离是80cm.如果活动窗拉开xcm时,窗户的通风面积是ycm2.
(1)试确定这个函数的解析式并指出自变量x的取值范围;
(2)画出这个函数的图象.
图3-4
25.某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据如下表:
砝码的质量(x克) 0 50 100 150 200 250 300 400 500
指针位置(y厘米) 2 3 4 5 6 7 7.5 7.5 7.5
(1)求出y与x的函数关系式;
(2)y关于x的函数图象是( )
图6-5
26.气温随着高度的增加而下降,下降的一般规律是从地面到高空11km处,每升高1km,气温下降6℃.高于11km时,气温几乎不再变化,设地面的气温为38℃,高空中xkm的气温为y℃.当0≤x≤11时,求y与x之间的关系式.
27.我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图6-6所示.
(1)观察图象,求出函数在不同范围内的解析式;
(2)说出自来水公司在这两个用水范围内的收费标准;
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
图6-6
提高练习
1.一次函数的图象过点A(5,3)且平行于直线y=3x-,则这个函数的解析式为________.
2. 一次函数与的图象如图,则下列结论:
①;②;③当时,中,正确的个数是( )
A.0 B.1 C.2 D.3
3.已知一次函数图象经过点(2,3),且与y轴交点的纵坐标为4,则这个函数的表达式是____.
4、一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点 B(3,3),则光线从A点到B点经过的路线长是 ;直线BC的解析式为 .
5. 若 ab>0,bc<0,则直线y=-x-不通过( )
A.第一象限 B.第一象限 C.第三象限 D.第四象限
6. 已知一次函数y= x+m和y= -x+n的图象都经过点A(-2,0)且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
7.已知函数的图象如图,则的图象可能是( )
9. 如图(1),在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至
点D停止.设点P运动的路程为,△ABP的面积为y,如果y关于x的函
数图象如图(2)所示,则△BCD的面积是( )
A.3 B.4 C.5 D.6
10. 如图,在中学生耐力测试比赛中,甲、乙两学生测试的路程s (米)与时间t (秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
A.乙比甲先到终点
B.乙测试的速度随时间增加而增大
C.比赛到29.4秒时,两人出发后第一次相遇
D.比赛全程甲测试速度始终比乙测试速度快
11. 小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达
点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.
下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保
持和去上班时一致,那么他从单位到家门口需要的时间是( )
A.12分钟 B.15分钟 C.25分钟 D.27分钟
12、如右图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是( )
13、如图1,在矩形中,动点从点出发,沿→→→方向运动至点处停止.设点运动的路程为,的面积为,如果关于的函数图象如图2所示,则当时,点应运动到( )
A.处 B.处 C.处 D.处
14. 求函数与x轴、y轴的交点坐标,并求这条直线与两坐标轴围成的三角形的面积.
15、已知两直线y1=2x-3,y2=6-x(1)在同一坐标系中作出它们的图象.(2)求它们的交点A的坐标.(3)根据图象指出x为何值时,y1>y2;x为何值时,y1<y2.(4)求这两条直线与x轴所围成的△ABC的面积.
16、已知一次函数y=kx+b的图像经过点A(0,2)和点B(-a,3)且点B在正比例函数y=-3x的图像上.(1) 求a的值;(2) 求一次函数的解析式.
17. 如图,直线l1、l2相交于点A,l1与x轴的交点坐标为(-1,0),l2与y轴的交点坐标为(0,-2),结合图象解答下列问题:
(1)求出直线l2表示的一次函数表达式;
(2)当x为何值时,l1、l2表示的两个一次函数的函数值都大于0?
18. 已知直线 y=x+2与直线 y= x+2交于 C点,直线y= -x+2与x轴交点为A,直线y= x+2与x轴交点为B.求△ABC的面积.
19.有一长方形AOBC纸片放在如图3-3所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出x=-5时,函数y的值;
(3)求出y=-5时,自变量x的值;
(4)画这个函数的图象;
(5)根据图象回答,当x从2减小到-3时,y的值是如何变化的?
图3-3
20.如图5-1,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的数据:
指距d(cm) 20 22
身高h(cm) 160 178
(1)求出h与d之间的函数关系式(不要求写出自变量d的取值范围);
(2)某人身高为196cm,一般情况下他的指距应是多少?
图5-1
21.某造纸厂污水处理的剩余污水随着时间的增加而减少,剩余污水量V(万米3)与污水处理时间t(天)的关系如图5-2所示,
(1)由图象求出剩余污水量V(万米3)与污水处理时间t(天)之间的函数解析式;
(2)污水处理连续10天,剩余污水还有多少万立方米?
(3)按照图中的规律,若想将全部污水处理干净,需要连续处理污水多少天?
(4)平均一天可处理污水多少万立方米?
图5-2
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
向左(右)平移p个单位
向上(下)平移p个单位
x
y
O
3
第2题图
第7题图
图(1)
2
O
5
x
A
B
C
P
D
图(2)
第9题图
1
2
3
4
1
2
y
s
O
1
2
3
4
1
2
y
s
O
s
1
2
3
4
1
2
y
s
O
1
2
3
4
1
2
y
O
A.
B.
C.
D.
Q
P
R
M
N
(图1)
(图2)
4
9
y
x
O
第 16 页 共 17 页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
