高中数学人教A版选修2-2课件:1.3.2函数的极值(共21张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-2课件:1.3.2函数的极值(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 688.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 13:50:28 | ||
图片预览







文档简介
(共20张PPT)
1.3.2 函数的极值
本节课的地位和作用
本节课是导数应用中的第二节(第一节是利用导数知识判断函数的单调性),学生们已经了解了导数的一些用途,思想中已有了一点运用导数的基本思想去分析和解决实际问题的意识,本节课将继续加强这方面的意识和能力的培养——利用导数知识求可导函数的极值.其后还有利用导数求函数的最值问题,因此本节课还要起到承上启下的作用.
1. 教学目标
(1)知识技能目标:
掌握函数极值的概念,会从几何图形直观理解函数的极值与导数的关系,增强学生的数形结合意识,提高思维水平;
掌握求可导函数的极值的一般方法;
了解可导函数极值点x0与f?(x0)=0的逻辑关系;
提高学生运用导数的基本思想去分析和解决问题的能力.
(3)情感与态度目标:
培养学生层层深入、一丝不苟研究事物的科学精神;
体会数学中的局部与整体的辨证关系.
2.教学重点和难点
重点:掌握求可导函数的极值的一般方法.
难点:x0为函数极值点与f ?(x0)?0 的逻辑关系.
3.教学方法与教学手段
师生互动探究式教学,遵循“教师为主导、学生为主体”的原则,结合高中学生的求知心理和已有的认知水平开展教学.由于学生对极限和导数的知识学习还谈不上深入细致(大学里还将继续学习),因此本节课的教学中更重视的是从感性认识到理性认识的探索过程,而略轻严格的理论证明过程,教师的主导作用和学生的主体作用必须得到的充分发挥.
利用多媒体辅助教学.电脑演示动画图形,直观形
象,便于学生观察.幻灯片打出重要结论,清楚明
了,节约时间,提高课堂效率.
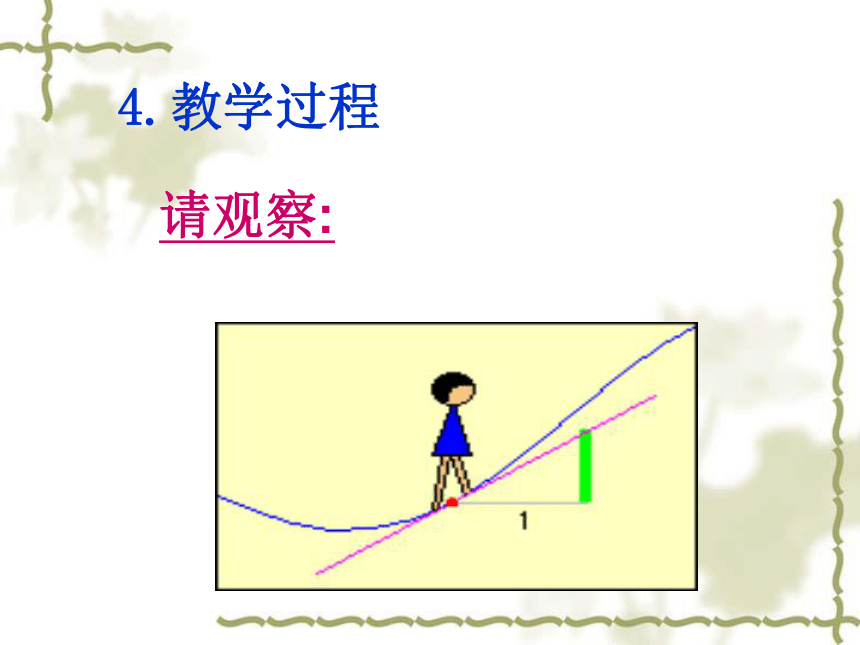
4.教学过程
请观察:
函数极值的定义
一般地,设函数f(x)在点x0附近有定义,
如果对x0附近的所有的点,都有f(x)﹤f (x0),我们就说f (x0)是函数f(x)的一个极大值,记作y极大值= f (x0);
如果对x0附近的所有的点,都有f(x)﹥f (x0),我们就说f (x0)是函数f(x)的一个极小值,记作y极小值=f (x0).
极大值与极小值同称为极值.
强调:极值是某一点附近的小区间而言的,是函数的局部性质,在整个定义区间内可能有多个极大值和极小值;极大值与极小值没有必然关系,极大值可能比极小值还小.
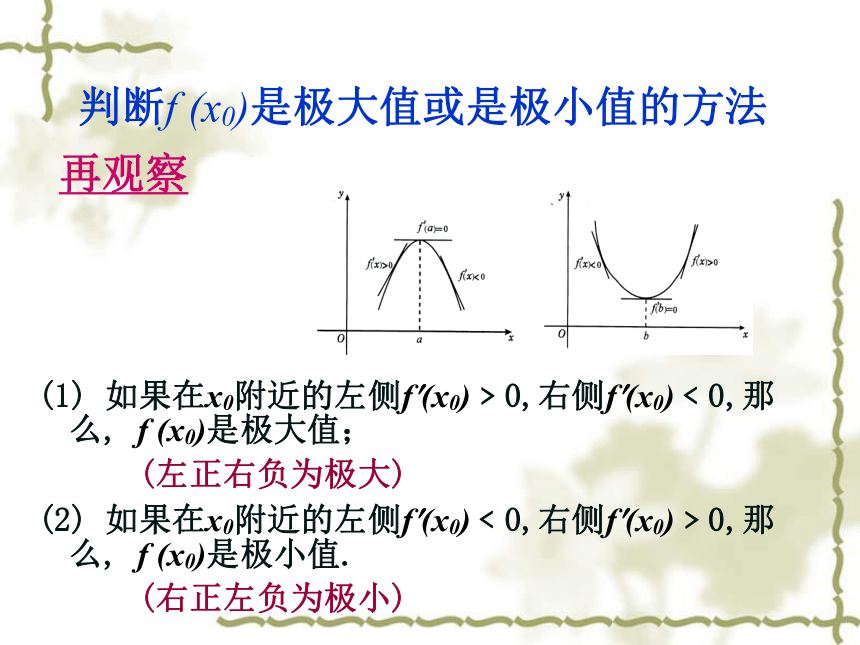
判断f (x0)是极大值或是极小值的方法
(1) 如果在x0附近的左侧f?(x0)﹥0,右侧f?(x0)﹤0,那么, f (x0)是极大值;
(左正右负为极大)
(2) 如果在x0附近的左侧f?(x0)﹤0,右侧f?(x0)﹥0,那么, f (x0)是极小值.
(右正左负为极小)
再观察
强调:要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.
解: ∵ f?(x)=x2- 4,由f?(x) =0解得 x1=2,x2=-2.
当x变化时, f?(x) 、 f(x)的变化情况如下表:
∴ 当x=2时,y极小值=28/3;当x=-2时, y极大值=-4/3.
应用1
x
f?(x)
f(x)
归纳 求可导函数的极值的步骤:
⑴求导数 f?(x);
⑵求方程 f?(x)=0的根;
⑶检查 f?(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取极大值;如果左负右正,那么f(x)在这个根处取极小值.
练一练 P130
(1) y极小值= f(7/2)=-25/4;
(2) y极大值= f(-5/4)=-25/8;
(3) y极大值= f(-3)=54, y极小值= f(3)=-54;
(4) y极大值= f(1)=2, y极小值= f(-1)=-2.
思考: (1) (2)问中的极值是该函数的最值吗?
探索: x =0是否为函数f(x)=x3的极值点?
若寻找函数极值点,可否只由f?(x)=0求得即可?
f?(x)=3x2 当f?(x)=0时,x =0,而x =0不是该函数的极值点.
f?(x0) =0 x0 是可导函数f(x)的极值点
应用2 求 y =(x2-1)3+1 的极值
解: ∵y? =6x(x2-1)2 = 6x(x-1)2(x+1)2
∴由y? =0解得 x1 =-1,x2 =0,x3 =1.
当x 变化时, y? 的符号如图:
∴当x =0时, y极小值=0.
x
y?
y
小结 可导函数的极值与导数的关系
函数的极值是就函数在某一点附近的小区间而言,在函数的整个定义区间内可能有多个极大值或极小值,且极大值不一定比极小值大.
点是极值点的充分不必要条件是在这点两侧的导数异号.点是极值点的必要不充分条件是在这点的导数为0.
研究 求函数f(x)= 的极值.
导函数f?(x0)不存在的点也可能是极值点 .
由图可知函数f(x)有极小值f(0) =0, f(2) =0,有极大值f(1)=1.
作业 P130 习题
选作 已知f(x)=ax 3+bx 2+ax(a≠0)在x= 1处取得极值,且f(1)=-1.(1)求a、b、c的值;(2)判断x = 1时函数取极大值还是极小值,并说明理由.
极值和最值的区别与联系
(局部与整体)
1.3.2 函数的极值
本节课的地位和作用
本节课是导数应用中的第二节(第一节是利用导数知识判断函数的单调性),学生们已经了解了导数的一些用途,思想中已有了一点运用导数的基本思想去分析和解决实际问题的意识,本节课将继续加强这方面的意识和能力的培养——利用导数知识求可导函数的极值.其后还有利用导数求函数的最值问题,因此本节课还要起到承上启下的作用.
1. 教学目标
(1)知识技能目标:
掌握函数极值的概念,会从几何图形直观理解函数的极值与导数的关系,增强学生的数形结合意识,提高思维水平;
掌握求可导函数的极值的一般方法;
了解可导函数极值点x0与f?(x0)=0的逻辑关系;
提高学生运用导数的基本思想去分析和解决问题的能力.
(3)情感与态度目标:
培养学生层层深入、一丝不苟研究事物的科学精神;
体会数学中的局部与整体的辨证关系.
2.教学重点和难点
重点:掌握求可导函数的极值的一般方法.
难点:x0为函数极值点与f ?(x0)?0 的逻辑关系.
3.教学方法与教学手段
师生互动探究式教学,遵循“教师为主导、学生为主体”的原则,结合高中学生的求知心理和已有的认知水平开展教学.由于学生对极限和导数的知识学习还谈不上深入细致(大学里还将继续学习),因此本节课的教学中更重视的是从感性认识到理性认识的探索过程,而略轻严格的理论证明过程,教师的主导作用和学生的主体作用必须得到的充分发挥.
利用多媒体辅助教学.电脑演示动画图形,直观形
象,便于学生观察.幻灯片打出重要结论,清楚明
了,节约时间,提高课堂效率.
4.教学过程
请观察:
函数极值的定义
一般地,设函数f(x)在点x0附近有定义,
如果对x0附近的所有的点,都有f(x)﹤f (x0),我们就说f (x0)是函数f(x)的一个极大值,记作y极大值= f (x0);
如果对x0附近的所有的点,都有f(x)﹥f (x0),我们就说f (x0)是函数f(x)的一个极小值,记作y极小值=f (x0).
极大值与极小值同称为极值.
强调:极值是某一点附近的小区间而言的,是函数的局部性质,在整个定义区间内可能有多个极大值和极小值;极大值与极小值没有必然关系,极大值可能比极小值还小.
判断f (x0)是极大值或是极小值的方法
(1) 如果在x0附近的左侧f?(x0)﹥0,右侧f?(x0)﹤0,那么, f (x0)是极大值;
(左正右负为极大)
(2) 如果在x0附近的左侧f?(x0)﹤0,右侧f?(x0)﹥0,那么, f (x0)是极小值.
(右正左负为极小)
再观察
强调:要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.
解: ∵ f?(x)=x2- 4,由f?(x) =0解得 x1=2,x2=-2.
当x变化时, f?(x) 、 f(x)的变化情况如下表:
∴ 当x=2时,y极小值=28/3;当x=-2时, y极大值=-4/3.
应用1
x
f?(x)
f(x)
归纳 求可导函数的极值的步骤:
⑴求导数 f?(x);
⑵求方程 f?(x)=0的根;
⑶检查 f?(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取极大值;如果左负右正,那么f(x)在这个根处取极小值.
练一练 P130
(1) y极小值= f(7/2)=-25/4;
(2) y极大值= f(-5/4)=-25/8;
(3) y极大值= f(-3)=54, y极小值= f(3)=-54;
(4) y极大值= f(1)=2, y极小值= f(-1)=-2.
思考: (1) (2)问中的极值是该函数的最值吗?
探索: x =0是否为函数f(x)=x3的极值点?
若寻找函数极值点,可否只由f?(x)=0求得即可?
f?(x)=3x2 当f?(x)=0时,x =0,而x =0不是该函数的极值点.
f?(x0) =0 x0 是可导函数f(x)的极值点
应用2 求 y =(x2-1)3+1 的极值
解: ∵y? =6x(x2-1)2 = 6x(x-1)2(x+1)2
∴由y? =0解得 x1 =-1,x2 =0,x3 =1.
当x 变化时, y? 的符号如图:
∴当x =0时, y极小值=0.
x
y?
y
小结 可导函数的极值与导数的关系
函数的极值是就函数在某一点附近的小区间而言,在函数的整个定义区间内可能有多个极大值或极小值,且极大值不一定比极小值大.
点是极值点的充分不必要条件是在这点两侧的导数异号.点是极值点的必要不充分条件是在这点的导数为0.
研究 求函数f(x)= 的极值.
导函数f?(x0)不存在的点也可能是极值点 .
由图可知函数f(x)有极小值f(0) =0, f(2) =0,有极大值f(1)=1.
作业 P130 习题
选作 已知f(x)=ax 3+bx 2+ax(a≠0)在x= 1处取得极值,且f(1)=-1.(1)求a、b、c的值;(2)判断x = 1时函数取极大值还是极小值,并说明理由.
极值和最值的区别与联系
(局部与整体)
