高中数学选修2-1课件:3.1.3空间向量的数量积运算 (共22张PPT)
文档属性
| 名称 | 高中数学选修2-1课件:3.1.3空间向量的数量积运算 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 16:25:26 | ||
图片预览





文档简介
(共22张PPT)
高二数学 选修2-1 第三章 空间向量与立体几何
课题
3.1.3空间向量的
数量积运算
标题
讲授新课
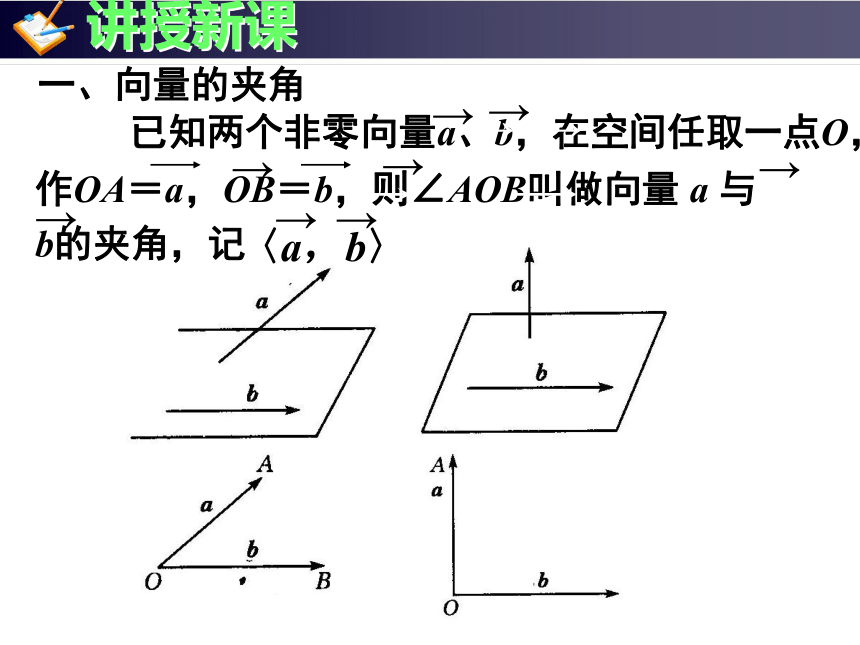
一、向量的夹角
已知两个非零向量a、b,在空间任取一点O,作OA=a,OB=b,则∠AOB叫做向量 a 与
b的夹角,记
→
→
→
→
→
→
一、向量的夹角概念
→
→
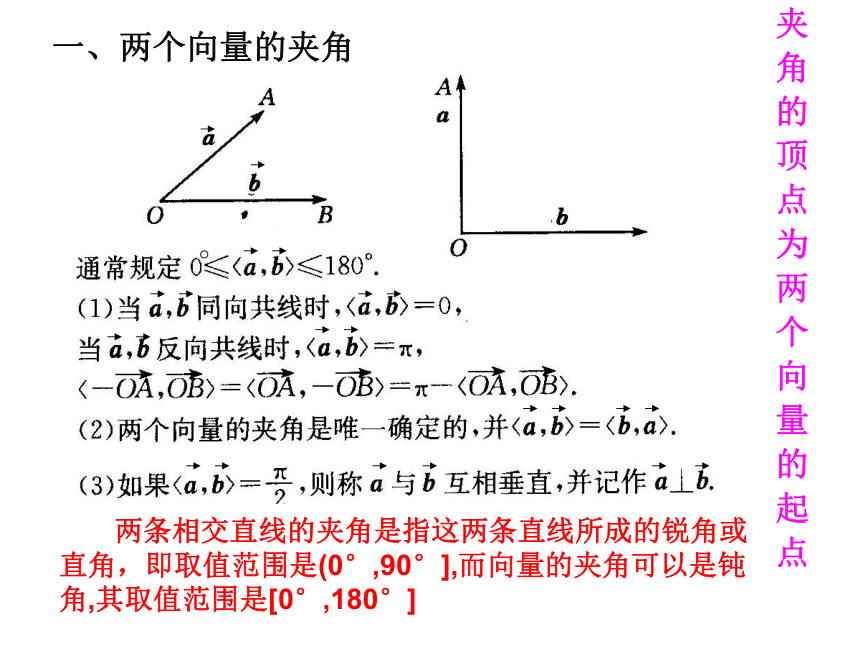
一、两个向量的夹角
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
夹
角
的
顶
点
为
两
个
向
量
的
起
点
一、向量的夹角概念
练习1
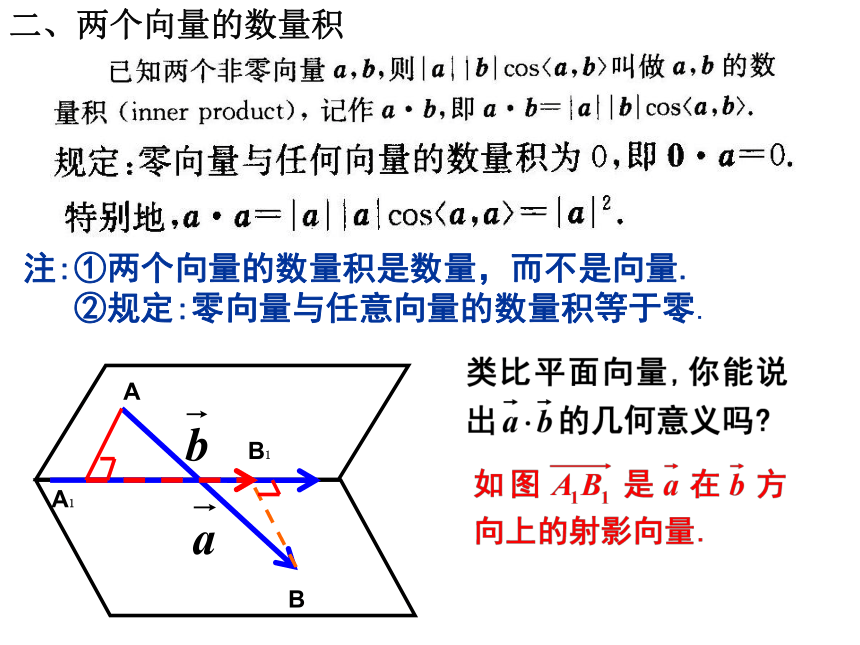
二、两个向量的数量积
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积等于零.
B
A
二、两个向量的数量积
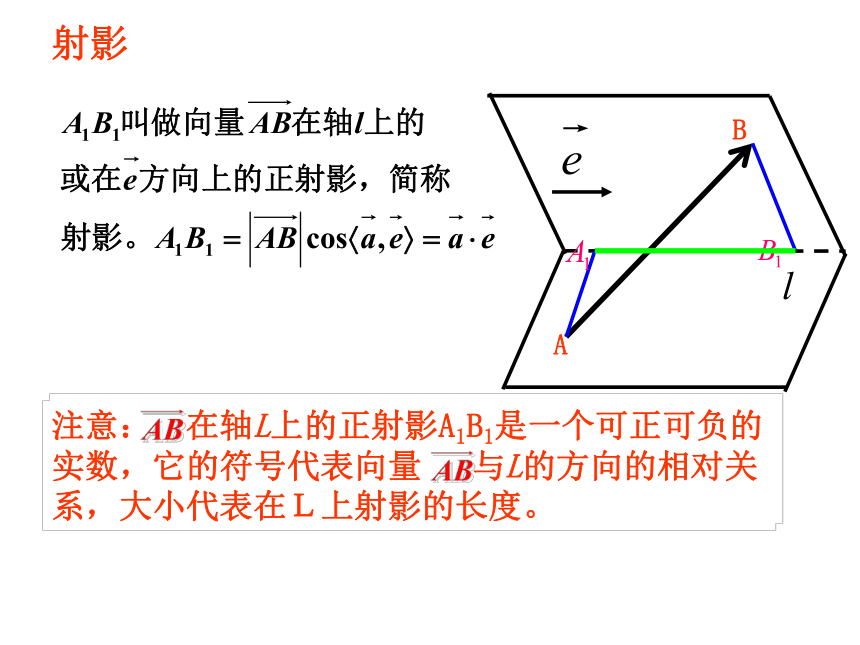
射影
注意: 在轴L上的正射影A1B1是一个可正可负的实数,它的符号代表向量 与L的方向的相对关系,大小代表在L上射影的长度。
A
B
射影
三、空间两个向量的数量积的性质
(1)空间向量的数量积具有和平面向量的数量积完全相
同的性质.
(2)性质(2)是用来判断两个向量是否垂直,性质3)是
求向量的长度(模)的依据;性质(5)是用来求两个
向量的夹角.
(3)性质(3)是实数与向量之间转化的依据.
三、空间向量的数量积性质
四、空间向量数量积的运算律
与平面向量一样,空间向量的数量积满足如下运算律:
向量数量积的运算适合乘法结合律吗?
即(a?b)c一定等于a(b·c)吗?
或
四、空间向量数量积的运算律
a
b
c
结论
已知空间向量a,b满足|a|=4,|b|=8,a与b的夹角是150°,计算:(1)(a+2b)·(2a-b);(2)|4a一2b|.
练习2
综合
分析
数形结合
妙!
练习3
在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B,D间的距离.
练习4
练习5
空间向量的运用还经常用来判定空间垂直关系,证两直线垂直线常可转化为证明以这两条线段对应的向量的数量积为零.
例题1
证明:
为
逆命题成立吗?
例题1的证明
分析:同样可用向量,证明思路几乎一样.
例题1的逆命题
例题1逆命题解答过程
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.
例2:(试用向量方法证明直线与平面垂直的判定定理)
已知直线m ,n是平面 内的两条相交直线,
如果 ⊥m, ⊥n,求证: ⊥ .
m
n
取已知平面内的任一条直线 g ,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件?要证的目标可以转化为向量的什么目标?怎样建立向量的条件与向量的目标的联系?
共面向量定理,有了!ye!
例题2
例2:已知直线m ,n是平面 内的两条相交直线,
如果 ⊥m, ⊥n,求证: ⊥ .
例题2的答案
n
到目前为止,我们可以利用向量数量积
解决立体几何中的以下几类问题:
1、证明两直线垂直。
2、求两点之间的距离或线段长度。
3、证明线面垂直。
4、求两直线所成角的余弦值等等。
小结
课本P97——习题3.1A组3T、4T、5T.
作业
课本P92——练习1T、3T .
高二数学 选修2-1 第三章 空间向量与立体几何
课题
3.1.3空间向量的
数量积运算
标题
讲授新课
一、向量的夹角
已知两个非零向量a、b,在空间任取一点O,作OA=a,OB=b,则∠AOB叫做向量 a 与
b的夹角,记
→
→
→
→
→
→
一、向量的夹角概念
→
→
一、两个向量的夹角
两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]
夹
角
的
顶
点
为
两
个
向
量
的
起
点
一、向量的夹角概念
练习1
二、两个向量的数量积
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积等于零.
B
A
二、两个向量的数量积
射影
注意: 在轴L上的正射影A1B1是一个可正可负的实数,它的符号代表向量 与L的方向的相对关系,大小代表在L上射影的长度。
A
B
射影
三、空间两个向量的数量积的性质
(1)空间向量的数量积具有和平面向量的数量积完全相
同的性质.
(2)性质(2)是用来判断两个向量是否垂直,性质3)是
求向量的长度(模)的依据;性质(5)是用来求两个
向量的夹角.
(3)性质(3)是实数与向量之间转化的依据.
三、空间向量的数量积性质
四、空间向量数量积的运算律
与平面向量一样,空间向量的数量积满足如下运算律:
向量数量积的运算适合乘法结合律吗?
即(a?b)c一定等于a(b·c)吗?
或
四、空间向量数量积的运算律
a
b
c
结论
已知空间向量a,b满足|a|=4,|b|=8,a与b的夹角是150°,计算:(1)(a+2b)·(2a-b);(2)|4a一2b|.
练习2
综合
分析
数形结合
妙!
练习3
在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B,D间的距离.
练习4
练习5
空间向量的运用还经常用来判定空间垂直关系,证两直线垂直线常可转化为证明以这两条线段对应的向量的数量积为零.
例题1
证明:
为
逆命题成立吗?
例题1的证明
分析:同样可用向量,证明思路几乎一样.
例题1的逆命题
例题1逆命题解答过程
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.
例2:(试用向量方法证明直线与平面垂直的判定定理)
已知直线m ,n是平面 内的两条相交直线,
如果 ⊥m, ⊥n,求证: ⊥ .
m
n
取已知平面内的任一条直线 g ,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件?要证的目标可以转化为向量的什么目标?怎样建立向量的条件与向量的目标的联系?
共面向量定理,有了!ye!
例题2
例2:已知直线m ,n是平面 内的两条相交直线,
如果 ⊥m, ⊥n,求证: ⊥ .
例题2的答案
n
到目前为止,我们可以利用向量数量积
解决立体几何中的以下几类问题:
1、证明两直线垂直。
2、求两点之间的距离或线段长度。
3、证明线面垂直。
4、求两直线所成角的余弦值等等。
小结
课本P97——习题3.1A组3T、4T、5T.
作业
课本P92——练习1T、3T .
