高中数学选修2-2课件:1.7定积分的简单应用体积 (共17张PPT)
文档属性
| 名称 | 高中数学选修2-2课件:1.7定积分的简单应用体积 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 474.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 16:30:55 | ||
图片预览






文档简介
(共17张PPT)
利用定积分求简单几何体的体积
高二数学备课组
1.体会利用定积分求体积的思想方法.
2.会利用定积分求简单几何体的体积.
3.体会极限思想的应用.
【核心扫描】
1.利用定积分求简单几何体的体积.(重点)
2.常与旋转体的概念等综合考查.(重点、难点)
【课标要求】
导
提示 本节定积分在几何中主要是求平面图形的面积,类似求面积,也可以利用定积分求空间几何体的体积,一般情况下,其旋转轴为x轴,根据旋转体的定义,旋转体的形成有两个要素:一是被旋转的平面图形,二是旋转轴.柱、锥、球等旋转体中被旋转的平面图形都是直线或圆弧,而在利用定积分求旋转体的体积问题中则是一般的曲线.
如何类比平面图形的面积的求法求几何体的体积?
思
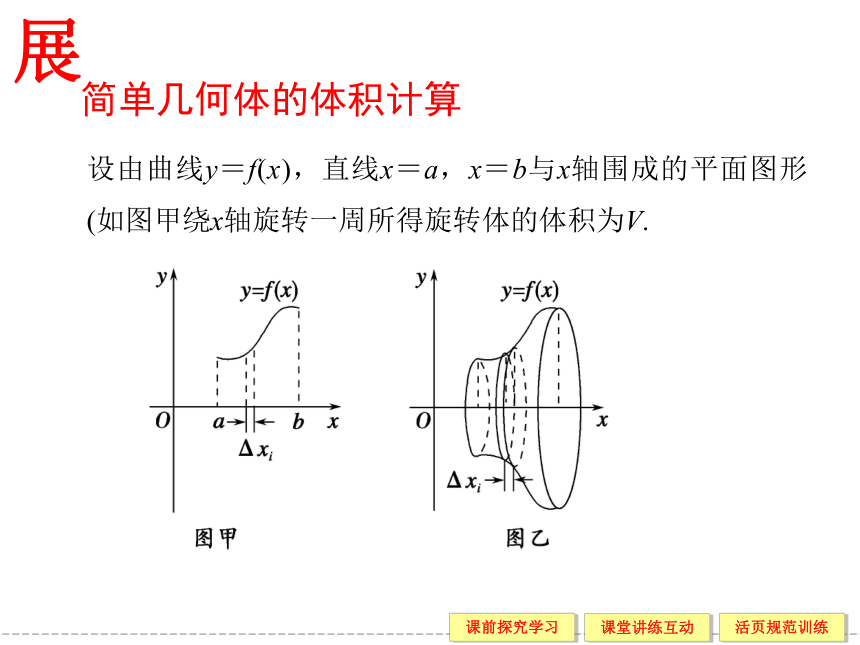
设由曲线y=f(x),直线x=a,x=b与x轴围成的平面图形(如图甲绕x轴旋转一周所得旋转体的体积为V.
简单几何体的体积计算
展
在区间[a,b]内插入n-1个分点,使a=x0<x1<x2<…<xn-1<xn=1,把曲线y=f(x),a≤x≤b分割成n个垂直于x轴的“小长条”,如图甲所示.设第i个“小长条”的宽是Δxi=xi-xi-1,i=1,2,…,n.这个“小长条”绕x轴旋转一周就得到一个厚度是Δxi的小圆片,如图乙所示.当Δxi很小时,第i个小圆片近似于底面半径为yi=f(xi)的小圆柱,因此,第i个小圆台的体积Vi近似为Vi=πf2(xi)Δxi.
该几何体的体积V等于所有小圆柱的体积和
V≈π[f2(x1)Δx1+f2(x2)Δx2+…+f2(xi)Δxi+…+f2(xn)Δxn].
这个问题是积分问题,则有
得到一个几何体,求它的体积.
[思路探索] 由旋转体体积的求法可知,先建立平面直角坐标系,写出正方形旋转轴对边的方程,确定积分上、下限,确定被积函数即可求出体积.
例1: 给定一个边长为a的正方形,绕其一边旋转一周,
[思路探索] 解答本题可先由解析式求出交点坐标.把组合体分开来求体积.
例2 、如图,求由抛物线y2=8x(y>0)与直线x+y-6=0
及y=0所围成的图形绕x轴旋转一周所得几何体的体积.
解决组合体的体积问题,关键是对其构造进行剖析,分解成几个简单几何体体积的和或差,然后,分别利用定积分求其体积.
审题指导 解题的关键是把所求旋转体体积看作两个旋转体体积之差.
(1)简单旋转体体积的求解步骤
①画出旋转前的平面图形和旋转体的图形;
②确定轴截面图形的范围,即求交点坐标,确定积分上、下限;
③确定被积变量、被积函数、体积公式类型;
④求出定积分,即旋转体的体积.
简单旋转体体积求法及步骤
方法一:特殊图形的体积公式法
方法二:定积分法
评
1 .如图所示,给定直角边为a的等腰直角三角形,绕
y轴旋转一周,求形成的几何体的体积.
检
形绕x轴旋转一周所得旋转体的体积.
2 、求由曲线y=2x,直线x=1与x轴围成的平面图
利用定积分求简单几何体的体积
高二数学备课组
1.体会利用定积分求体积的思想方法.
2.会利用定积分求简单几何体的体积.
3.体会极限思想的应用.
【核心扫描】
1.利用定积分求简单几何体的体积.(重点)
2.常与旋转体的概念等综合考查.(重点、难点)
【课标要求】
导
提示 本节定积分在几何中主要是求平面图形的面积,类似求面积,也可以利用定积分求空间几何体的体积,一般情况下,其旋转轴为x轴,根据旋转体的定义,旋转体的形成有两个要素:一是被旋转的平面图形,二是旋转轴.柱、锥、球等旋转体中被旋转的平面图形都是直线或圆弧,而在利用定积分求旋转体的体积问题中则是一般的曲线.
如何类比平面图形的面积的求法求几何体的体积?
思
设由曲线y=f(x),直线x=a,x=b与x轴围成的平面图形(如图甲绕x轴旋转一周所得旋转体的体积为V.
简单几何体的体积计算
展
在区间[a,b]内插入n-1个分点,使a=x0<x1<x2<…<xn-1<xn=1,把曲线y=f(x),a≤x≤b分割成n个垂直于x轴的“小长条”,如图甲所示.设第i个“小长条”的宽是Δxi=xi-xi-1,i=1,2,…,n.这个“小长条”绕x轴旋转一周就得到一个厚度是Δxi的小圆片,如图乙所示.当Δxi很小时,第i个小圆片近似于底面半径为yi=f(xi)的小圆柱,因此,第i个小圆台的体积Vi近似为Vi=πf2(xi)Δxi.
该几何体的体积V等于所有小圆柱的体积和
V≈π[f2(x1)Δx1+f2(x2)Δx2+…+f2(xi)Δxi+…+f2(xn)Δxn].
这个问题是积分问题,则有
得到一个几何体,求它的体积.
[思路探索] 由旋转体体积的求法可知,先建立平面直角坐标系,写出正方形旋转轴对边的方程,确定积分上、下限,确定被积函数即可求出体积.
例1: 给定一个边长为a的正方形,绕其一边旋转一周,
[思路探索] 解答本题可先由解析式求出交点坐标.把组合体分开来求体积.
例2 、如图,求由抛物线y2=8x(y>0)与直线x+y-6=0
及y=0所围成的图形绕x轴旋转一周所得几何体的体积.
解决组合体的体积问题,关键是对其构造进行剖析,分解成几个简单几何体体积的和或差,然后,分别利用定积分求其体积.
审题指导 解题的关键是把所求旋转体体积看作两个旋转体体积之差.
(1)简单旋转体体积的求解步骤
①画出旋转前的平面图形和旋转体的图形;
②确定轴截面图形的范围,即求交点坐标,确定积分上、下限;
③确定被积变量、被积函数、体积公式类型;
④求出定积分,即旋转体的体积.
简单旋转体体积求法及步骤
方法一:特殊图形的体积公式法
方法二:定积分法
评
1 .如图所示,给定直角边为a的等腰直角三角形,绕
y轴旋转一周,求形成的几何体的体积.
检
形绕x轴旋转一周所得旋转体的体积.
2 、求由曲线y=2x,直线x=1与x轴围成的平面图
