高中数学选修2-2课件:3.1.1数系的扩充与复数的引入 (共21张PPT)
文档属性
| 名称 | 高中数学选修2-2课件:3.1.1数系的扩充与复数的引入 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-03 16:31:23 | ||
图片预览




文档简介
(共21张PPT)
5.1.1数系的扩充与复数的引入
高二数学备课组
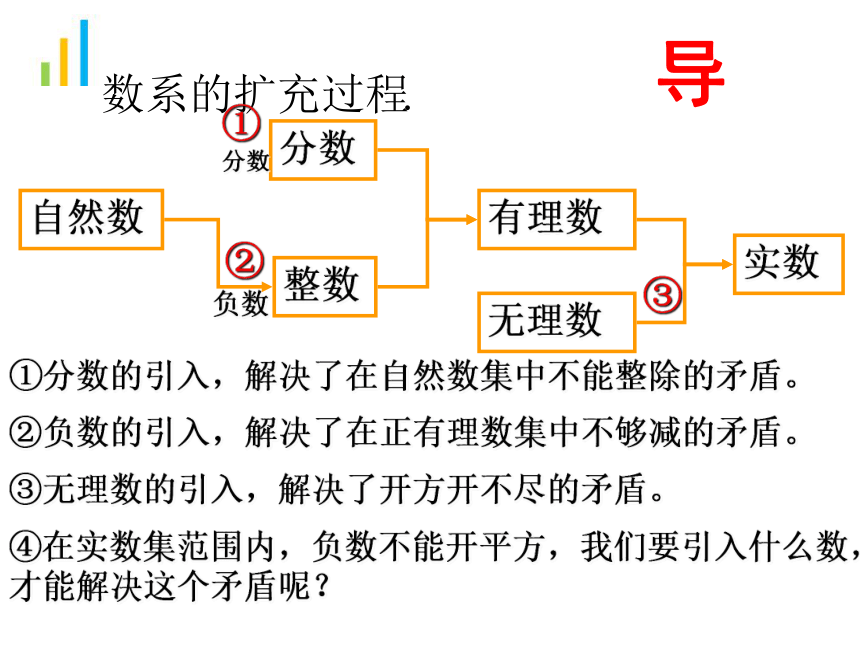
自然数
分数
有理数
无理数
实数
①分数的引入,解决了在自然数集中不能整除的矛盾。
③
整数
②负数的引入,解决了在正有理数集中不够减的矛盾。
③无理数的引入,解决了开方开不尽的矛盾。
④在实数集范围内,负数不能开平方,我们要引入什么数,才能解决这个矛盾呢?
导
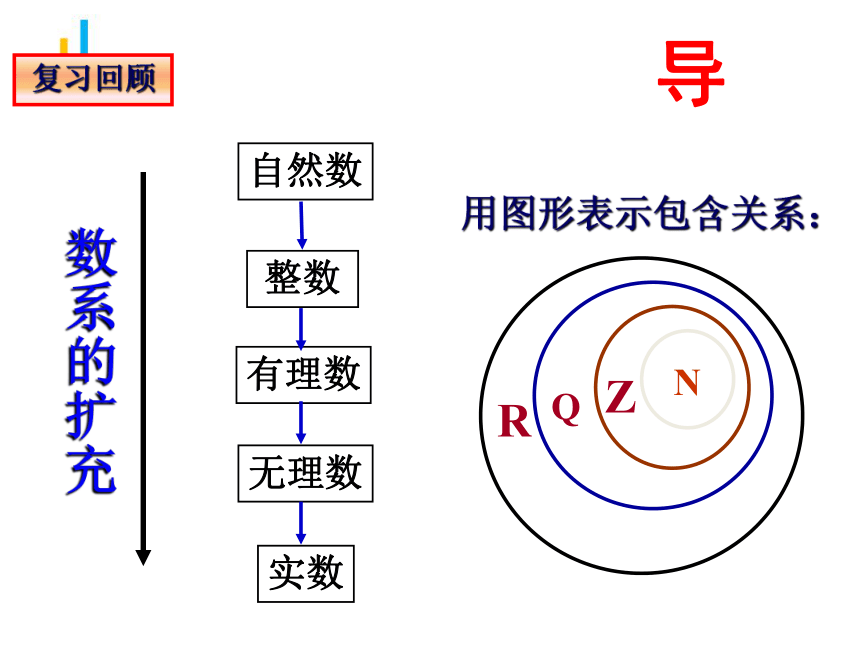
数系的扩充
用图形表示包含关系:
复习回顾
导
知识引入
导
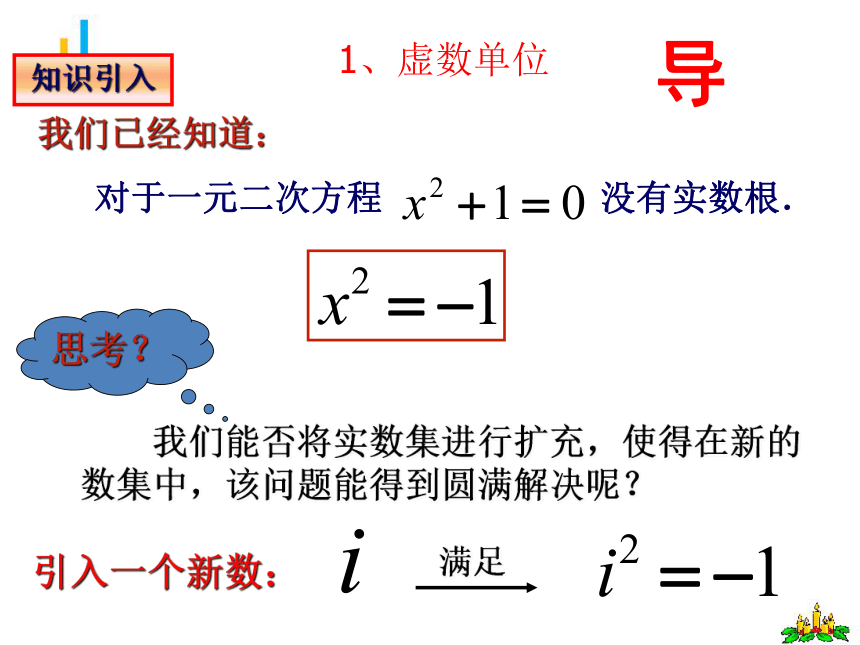
1、虚数单位
现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。
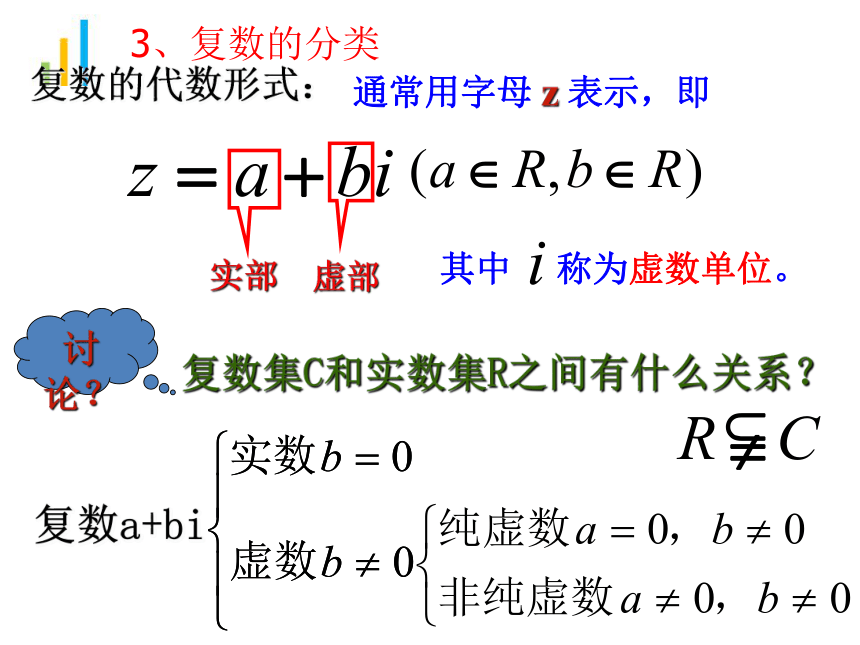
形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集,
一般用字母C表示 .
2、复数的概念和复数集
复数的代数形式:
(3)其中a=0且b≠0时称为纯虚数。
注意:
(2)当b≠0时,a+bi是虚数,
(1)当b=0时,a+bi就是实数,
如:1,2.5,-1/2
如:
如:
复数的代数形式:
复数a+bi
3、复数的分类
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
复数相等的充要条件
4、复数相等
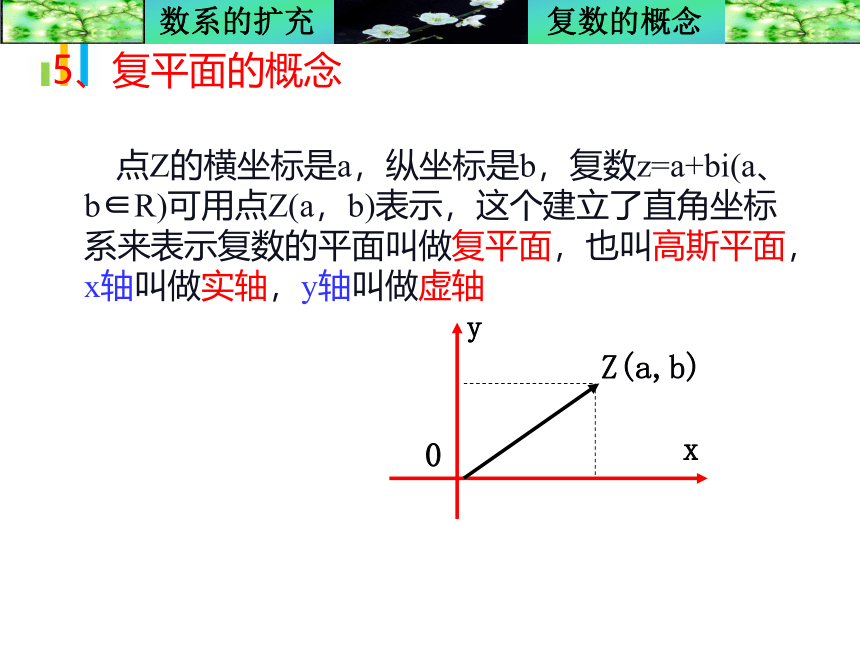
5、复平面的概念
点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,x轴叫做实轴,y轴叫做虚轴
5、复平面的概念
对于任何一个复数z=a+bi(a、b∈R),由复数相等的定义可知,可以由一个有序实数对(a,b)惟一确定,如z=3+2i可以由有序实数对(3,2)确定,又如z=-2+i可以由有序实数对(-2,1)来确定;又因为有序实数对(a,b)与平面直角坐标系中的点是一一对应的,如有序实数对(3,2)它与平面直角坐标系中的点A,横坐标为3,纵坐标为2,建立了一一对应的关系
由此可知,复数集与复平面坐标系中的点集之间可以建立一一对应的关系.
注:
(1)实轴上的点都表示实数;
(2)对于虚轴上的点要除原点外,因为
原点对应的有序实数对为(0,0), 它所确
定的复数是z=0+0i=0表示是实数.故除了原
点外,虚轴上的点都表示纯虚数;
(3)非纯虚数对应的点在四个象限,例
如点(-2,3)表示的复数是-2+3i,z=-5
-3i对应的点(-5,-3)在第三象限等等.
1.实数绝对值的几何意义?
2.复数的模 (或绝对值)的几何意义?
实数a在数轴上所对应的点A到原点O的距离.
|a| = |OA|
复数的模
探究一: 实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
议展
变式1:当m为何实数时,复数
(1)实数 (2)虚数 (3)纯虚数
(3)m=-2
两个复数相等应满足什么条件呢?
思考?
探究二
议展
探究三:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。
一种重要的数学思想:数形结合思想
议展
变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-6)-2(m2+m-2)+4=0,
∴m=1或m=-2。
求证:对一切实数m,此复数所对应的点不可能位于第四象限.
变式二:已知复数z=(m2+m-6)+(m2+m-2)i,
用反证法证明
1、若x,y为实数,且
求x,y.
x=0,y=2
2
检
1.虚数单位i的引入;i2??1
5.1.1数系的扩充与复数的引入
高二数学备课组
自然数
分数
有理数
无理数
实数
①分数的引入,解决了在自然数集中不能整除的矛盾。
③
整数
②负数的引入,解决了在正有理数集中不够减的矛盾。
③无理数的引入,解决了开方开不尽的矛盾。
④在实数集范围内,负数不能开平方,我们要引入什么数,才能解决这个矛盾呢?
导
数系的扩充
用图形表示包含关系:
复习回顾
导
知识引入
导
1、虚数单位
现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。
形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集,
一般用字母C表示 .
2、复数的概念和复数集
复数的代数形式:
(3)其中a=0且b≠0时称为纯虚数。
注意:
(2)当b≠0时,a+bi是虚数,
(1)当b=0时,a+bi就是实数,
如:1,2.5,-1/2
如:
如:
复数的代数形式:
复数a+bi
3、复数的分类
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
复数相等的充要条件
4、复数相等
5、复平面的概念
点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,x轴叫做实轴,y轴叫做虚轴
5、复平面的概念
对于任何一个复数z=a+bi(a、b∈R),由复数相等的定义可知,可以由一个有序实数对(a,b)惟一确定,如z=3+2i可以由有序实数对(3,2)确定,又如z=-2+i可以由有序实数对(-2,1)来确定;又因为有序实数对(a,b)与平面直角坐标系中的点是一一对应的,如有序实数对(3,2)它与平面直角坐标系中的点A,横坐标为3,纵坐标为2,建立了一一对应的关系
由此可知,复数集与复平面坐标系中的点集之间可以建立一一对应的关系.
注:
(1)实轴上的点都表示实数;
(2)对于虚轴上的点要除原点外,因为
原点对应的有序实数对为(0,0), 它所确
定的复数是z=0+0i=0表示是实数.故除了原
点外,虚轴上的点都表示纯虚数;
(3)非纯虚数对应的点在四个象限,例
如点(-2,3)表示的复数是-2+3i,z=-5
-3i对应的点(-5,-3)在第三象限等等.
1.实数绝对值的几何意义?
2.复数的模 (或绝对值)的几何意义?
实数a在数轴上所对应的点A到原点O的距离.
|a| = |OA|
复数的模
探究一: 实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
议展
变式1:当m为何实数时,复数
(1)实数 (2)虚数 (3)纯虚数
(3)m=-2
两个复数相等应满足什么条件呢?
思考?
探究二
议展
探究三:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。
一种重要的数学思想:数形结合思想
议展
变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-6)-2(m2+m-2)+4=0,
∴m=1或m=-2。
求证:对一切实数m,此复数所对应的点不可能位于第四象限.
变式二:已知复数z=(m2+m-6)+(m2+m-2)i,
用反证法证明
1、若x,y为实数,且
求x,y.
x=0,y=2
2
检
1.虚数单位i的引入;i2??1
