高中数学选修2-2课件:5.2复数的四则运算 (共24张PPT)
文档属性
| 名称 | 高中数学选修2-2课件:5.2复数的四则运算 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-04 09:25:01 | ||
图片预览








文档简介
(共24张PPT)
5.2 复数的四则运算
及加减法几何意义
高二数学备课组
【学习目标】
1.掌握复数的四则运算,了解复数运算的交换律、 结合律、分配律,理解复数加法减法的几何意义。(重点)
2.复数问题转化为实数问题的思想方法,复数加法、减法的几何意义。(重难点)
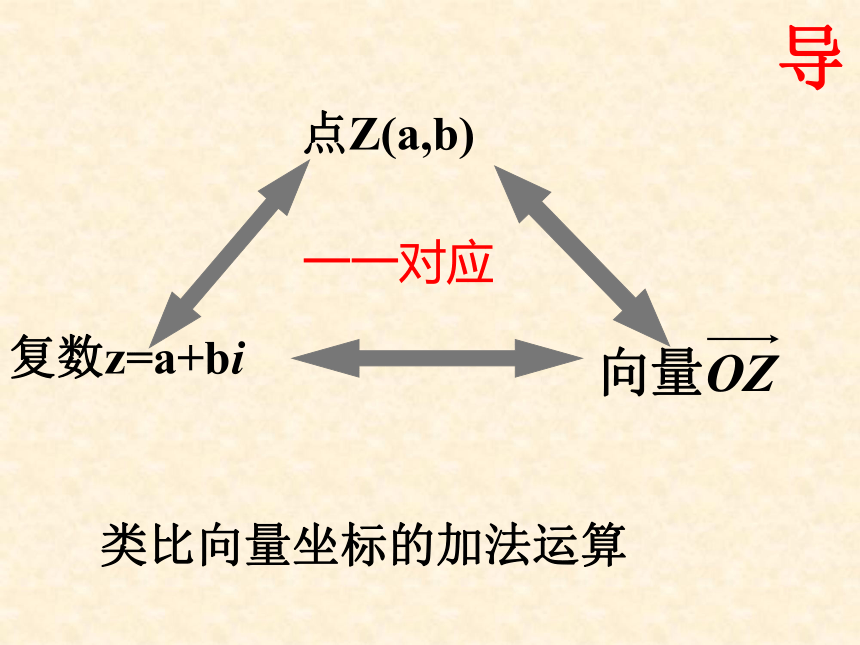
点Z(a,b)
复数z=a+bi
一一对应
类比向量坐标的加法运算
导
一、复数加、减法运算法则
设z1=a+bi,z2=c+di是任意两个复数,
则(a+bi)+(c+di)=
(a+c)+(b+d)i
规定复数的减法是加法的逆运算
把满足(c+di)+(x+yi)=a+bi 的复数x+yi叫做复数a+bi减去复数c+di的差,记作: x+yi=(a+bi)- (c+di)
导
由(c+di)+(x+yi)=a+bi,根据复数
相等的定义,得
c+x=a,d+y=b
即x=a-c,y=b-d
从而得到复数的减法法则为:
(a+bi) - (c+di) =(a-c)+(b-d)i
由上可知:复数的加减法就是把复数的实部与实部、虚部与虚部分别相加减。
(a+bi) ?(c+di) =(a ? c)+(b ? d)i
导
说明:
1、复数加(减)法法则是实数加(减)法法则的扩充,当两个复数均为实数时,与实数加(减)法法则一致。
2、复数的加(减)法法则体现了——
复数运算转化为实数运算的思想方法。
3、加法的交换律与结合律也适用于复数的运算。
(a+bi) ?(c+di) =(a ? c)+(b ? d)i
导
二、复数的乘法与乘方运算
1.设z1=a+bi,z2=c+di,(a,b,c,d∈R),则
运算与多项式运算类似。
特征:两个复数的积仍然是一个复数。
z1z2=(a+bi)(c+di)
=ac+adi+bci+bdi2
=(ac-bd)+(ad+bc)i
导
2、复数的乘法满足交换律、结合律及乘法对加法的分配律。
(1)z1z2=z2z1 (交换律)
(2)(z1z2)z3=z1(z2z3) (结合律)
(3)z1(z2+z3)=z1z2+z1z3 (分配律)
导
说明:
3、共轭复数:
实部相等而虚部互为相反数的两个复数,叫做互为共轭复数,也称这两个复数互相共轭。
定义:
导
4、复数中正整数指数幂的运算律
(1) zmzn=zm+n
(2) (zm)n=zmn
(3) (z1z2)n=z1nz2n
导
把满足(c+di)(x+yi) =a+bi (c+di≠0) 的复数 x+yi 叫做复数 a+bi 除以复数c+di的商,
三、复数的除法
导
导
四、复数加、减法的几何意义
导
1、用图象表示出z=z1+z2的几何意义
平行四边形法则
三角形法则
导
Z2
三角形法则
减数
被减数
2、两复数差的几何意义
两个复数的差z2-z1与连结向量的终点,且指向被减数的向量对应。
由该图还可看出,两复数差的模|z2-z1|表示Z1Z2两点距离。
导
求值,并找出规律。
i1= i2=
i3= i4=
i5= i6=
i7= i8=
i4n+1= i4n+2=
i4n+3= i4n=
i
-1
-i
1
i4·i=i
i4·i2=i2=-1
i4·i3=i3=-i
i4·i4=i4=1
(i4) n·i=i
(i4) n·i2 =i2=-1
(i4) n·i3=i3=-i
(i4) n=1
其中:i4n+1= i i4n+2=-1 i4n+3=-i i4n=1
思
探究一 计算
(1) (5-6i)+(-2-i)-(3+4i);
(2) [(a+b)+(a-b)i]-[(a-b)-(a+b)i]
(2)2b+2ai
议、展
(1)-11i
探究二 计算
(1)(1-2i)(3+4i)(-2+i)
(2)(-12+5i)(12+5i)+
(1)-20+15i
(2)-177
议、展
两个特殊复数的乘方
探究三
议、展
小结:
探究四 计算
议、展
4-2i
(2)复数z1=1+2i,z2=-2+i,z3=-1-2i,它们在复平面上的对应点是一个正方形的三个顶点,求这个正方形的第四个顶点对应的复数。
2-i
检
5.2 复数的四则运算
及加减法几何意义
高二数学备课组
【学习目标】
1.掌握复数的四则运算,了解复数运算的交换律、 结合律、分配律,理解复数加法减法的几何意义。(重点)
2.复数问题转化为实数问题的思想方法,复数加法、减法的几何意义。(重难点)
点Z(a,b)
复数z=a+bi
一一对应
类比向量坐标的加法运算
导
一、复数加、减法运算法则
设z1=a+bi,z2=c+di是任意两个复数,
则(a+bi)+(c+di)=
(a+c)+(b+d)i
规定复数的减法是加法的逆运算
把满足(c+di)+(x+yi)=a+bi 的复数x+yi叫做复数a+bi减去复数c+di的差,记作: x+yi=(a+bi)- (c+di)
导
由(c+di)+(x+yi)=a+bi,根据复数
相等的定义,得
c+x=a,d+y=b
即x=a-c,y=b-d
从而得到复数的减法法则为:
(a+bi) - (c+di) =(a-c)+(b-d)i
由上可知:复数的加减法就是把复数的实部与实部、虚部与虚部分别相加减。
(a+bi) ?(c+di) =(a ? c)+(b ? d)i
导
说明:
1、复数加(减)法法则是实数加(减)法法则的扩充,当两个复数均为实数时,与实数加(减)法法则一致。
2、复数的加(减)法法则体现了——
复数运算转化为实数运算的思想方法。
3、加法的交换律与结合律也适用于复数的运算。
(a+bi) ?(c+di) =(a ? c)+(b ? d)i
导
二、复数的乘法与乘方运算
1.设z1=a+bi,z2=c+di,(a,b,c,d∈R),则
运算与多项式运算类似。
特征:两个复数的积仍然是一个复数。
z1z2=(a+bi)(c+di)
=ac+adi+bci+bdi2
=(ac-bd)+(ad+bc)i
导
2、复数的乘法满足交换律、结合律及乘法对加法的分配律。
(1)z1z2=z2z1 (交换律)
(2)(z1z2)z3=z1(z2z3) (结合律)
(3)z1(z2+z3)=z1z2+z1z3 (分配律)
导
说明:
3、共轭复数:
实部相等而虚部互为相反数的两个复数,叫做互为共轭复数,也称这两个复数互相共轭。
定义:
导
4、复数中正整数指数幂的运算律
(1) zmzn=zm+n
(2) (zm)n=zmn
(3) (z1z2)n=z1nz2n
导
把满足(c+di)(x+yi) =a+bi (c+di≠0) 的复数 x+yi 叫做复数 a+bi 除以复数c+di的商,
三、复数的除法
导
导
四、复数加、减法的几何意义
导
1、用图象表示出z=z1+z2的几何意义
平行四边形法则
三角形法则
导
Z2
三角形法则
减数
被减数
2、两复数差的几何意义
两个复数的差z2-z1与连结向量的终点,且指向被减数的向量对应。
由该图还可看出,两复数差的模|z2-z1|表示Z1Z2两点距离。
导
求值,并找出规律。
i1= i2=
i3= i4=
i5= i6=
i7= i8=
i4n+1= i4n+2=
i4n+3= i4n=
i
-1
-i
1
i4·i=i
i4·i2=i2=-1
i4·i3=i3=-i
i4·i4=i4=1
(i4) n·i=i
(i4) n·i2 =i2=-1
(i4) n·i3=i3=-i
(i4) n=1
其中:i4n+1= i i4n+2=-1 i4n+3=-i i4n=1
思
探究一 计算
(1) (5-6i)+(-2-i)-(3+4i);
(2) [(a+b)+(a-b)i]-[(a-b)-(a+b)i]
(2)2b+2ai
议、展
(1)-11i
探究二 计算
(1)(1-2i)(3+4i)(-2+i)
(2)(-12+5i)(12+5i)+
(1)-20+15i
(2)-177
议、展
两个特殊复数的乘方
探究三
议、展
小结:
探究四 计算
议、展
4-2i
(2)复数z1=1+2i,z2=-2+i,z3=-1-2i,它们在复平面上的对应点是一个正方形的三个顶点,求这个正方形的第四个顶点对应的复数。
2-i
检
