高中数学选修4-4课件:1.1平面直角坐标系与曲线方程 (共19张PPT)
文档属性
| 名称 | 高中数学选修4-4课件:1.1平面直角坐标系与曲线方程 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-04 09:35:18 | ||
图片预览






文档简介
(共19张PPT)
§1.1 平面直角坐标系与曲线方程
高二数学备课组
1? 数轴(直线坐标系):
2? 平面直角坐标系:
3? 空间直角坐标系:
任意
点P
实数x
有序实数对(x, y)
有序实数组(x, y, z)
? 建立坐标系目的是确定点的位置.
创建坐标系的基本原则:
(1) 任意一点都有确定的坐标与它对应;
(2) 依据一个点的坐标就能确定此点的位置.
? 求出此点在该坐标系中的坐标.
导
“曲线与方程”是解析几何的重要概念.
“在直角坐标系中,如果曲线C上的点与
一个二元方程f (x,y)=0的实解有如下关系:
1.曲线上的点的坐标都是这个方程的解;
2.以这个方程的解为坐标的点都是曲线上的点.
那末:“这个方程f(x,y)=0叫做曲线的方程;这条曲线叫做方程f(x,y)=0的曲线.”
如何理解?
导
1.曲线上的点的坐标都是这个方程的解; 2.以这个方程的解为坐标的点都是曲线上的点.
1 判断以下方程是否为曲线的方程:
(1) 经过点(3,0)且垂直于x 轴的直线
与∣x∣=3;
(2) 与坐标轴距离相等的点的集合
与x-y=0.
思
不是
不是
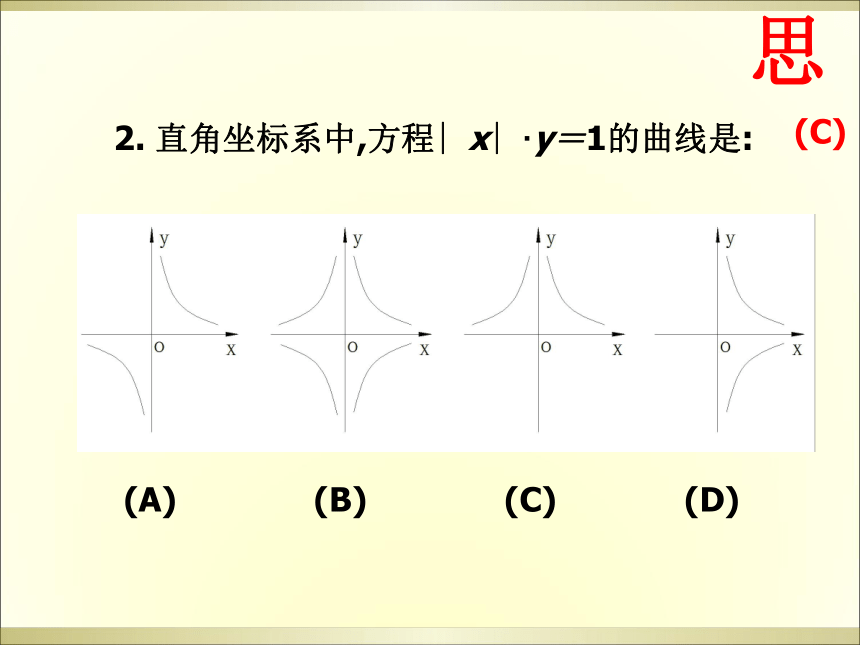
2. 直角坐标系中,方程∣x∣·y=1的曲线是:
(A) (B) (C) (D)
(C)
思
求曲线方程的一般方法步骤:坐标法
(1)建立适当的坐标系,用(x,y)表示曲线上
任意一点M的坐标
(2)写出适合条件P的点M的集合 P={M | p(M)};
(3) 用坐标表示条件p(M),列出方程 f(x,y)=0
(4) 化方程 f(x,y)=0为最简形式
(5)证明以化简后的方程的解为坐标的点都是
曲线上的点。
建系、设点
条件列式
坐标化
化简方程
检验
3、我们在必修课和选修2中学习过一些曲线方程,结合课本P2-3,如何求曲线方程?
思
1、点M(x,y)到定点F(5,0)的距离和它
到定直线l: 的距离的比是常数 ,
求点M的轨迹。
解:设d是点M到直线l的距离,
根据题意,
F
H
议、展
将上式两边平方,并化简得
9x2-16y2=144,
它是一条双曲线。
展
坐标法
在必修课和选修系列1,2中我们学习过如下一些曲线的方程:
①
②
③
④
⑤
议
定义法
共 12 页
*
3.过点P1(1,5)作直线交x轴于点A,过点P2(2,7)作直线P1A的垂线交y轴于点B,点M在线段AB上,且BM∶MA=1∶2,求动点M的轨迹方程.
相关点法
共 12 页
*
消参法
共 12 页
*
1.方程(x2-3)2+(y2-4)2=0表示的图形是( )
A.两个点 B.四个点
C.两条直线 D.四条直线
答案:B
检
共 12 页
*
2.已知直线l:x+y-3=0,曲线:(x-3)2+(y-2)2=2,则点M(2,1)( )
A.在直线l上,但不在曲线上
B.在直线l上,也在曲线上
C.不在直线l上,也不在曲线上
D.不在直线l上,但在曲线上
答案:B
解析:将M(2,1)代入直线方程,2+1-3=0,
将M(2,1)代入曲线方程,(2-3)2+(1-2)2=2,
故点M在l上,也在曲线上.
检
共 12 页
*
3、
检
共 12 页
*
解析:(1)方程 ,表示的曲线是以(2,0)为对称中心,焦点在x轴上,长轴长为6,焦距为 的椭圆.
(2)方程(x+2)2+(y-2)2=16表示的曲线是以(-2,2)为圆心,4为半径的圆.
(3)方程(2x+3y-5) =0表示直线2x+3y-5=0与射线x=4(x≥3).
(4)方程 ,可以看作点(x,y)到(2,0)的距离与到直线x=4的距离之比为2,故此方程表示以(2,0)为焦点,离心率为2的双曲线.
共 12 页
*
4.设动点P在直线x=1上,O为坐标原点,以OP为直角边,以点O为直角顶点作等腰Rt△OPQ,则动点Q的轨迹是( )
A.圆 B.两条平行直线
C.抛物线 D.双曲线
答案:B
坐标法
检
§1.1 平面直角坐标系与曲线方程
高二数学备课组
1? 数轴(直线坐标系):
2? 平面直角坐标系:
3? 空间直角坐标系:
任意
点P
实数x
有序实数对(x, y)
有序实数组(x, y, z)
? 建立坐标系目的是确定点的位置.
创建坐标系的基本原则:
(1) 任意一点都有确定的坐标与它对应;
(2) 依据一个点的坐标就能确定此点的位置.
? 求出此点在该坐标系中的坐标.
导
“曲线与方程”是解析几何的重要概念.
“在直角坐标系中,如果曲线C上的点与
一个二元方程f (x,y)=0的实解有如下关系:
1.曲线上的点的坐标都是这个方程的解;
2.以这个方程的解为坐标的点都是曲线上的点.
那末:“这个方程f(x,y)=0叫做曲线的方程;这条曲线叫做方程f(x,y)=0的曲线.”
如何理解?
导
1.曲线上的点的坐标都是这个方程的解; 2.以这个方程的解为坐标的点都是曲线上的点.
1 判断以下方程是否为曲线的方程:
(1) 经过点(3,0)且垂直于x 轴的直线
与∣x∣=3;
(2) 与坐标轴距离相等的点的集合
与x-y=0.
思
不是
不是
2. 直角坐标系中,方程∣x∣·y=1的曲线是:
(A) (B) (C) (D)
(C)
思
求曲线方程的一般方法步骤:坐标法
(1)建立适当的坐标系,用(x,y)表示曲线上
任意一点M的坐标
(2)写出适合条件P的点M的集合 P={M | p(M)};
(3) 用坐标表示条件p(M),列出方程 f(x,y)=0
(4) 化方程 f(x,y)=0为最简形式
(5)证明以化简后的方程的解为坐标的点都是
曲线上的点。
建系、设点
条件列式
坐标化
化简方程
检验
3、我们在必修课和选修2中学习过一些曲线方程,结合课本P2-3,如何求曲线方程?
思
1、点M(x,y)到定点F(5,0)的距离和它
到定直线l: 的距离的比是常数 ,
求点M的轨迹。
解:设d是点M到直线l的距离,
根据题意,
F
H
议、展
将上式两边平方,并化简得
9x2-16y2=144,
它是一条双曲线。
展
坐标法
在必修课和选修系列1,2中我们学习过如下一些曲线的方程:
①
②
③
④
⑤
议
定义法
共 12 页
*
3.过点P1(1,5)作直线交x轴于点A,过点P2(2,7)作直线P1A的垂线交y轴于点B,点M在线段AB上,且BM∶MA=1∶2,求动点M的轨迹方程.
相关点法
共 12 页
*
消参法
共 12 页
*
1.方程(x2-3)2+(y2-4)2=0表示的图形是( )
A.两个点 B.四个点
C.两条直线 D.四条直线
答案:B
检
共 12 页
*
2.已知直线l:x+y-3=0,曲线:(x-3)2+(y-2)2=2,则点M(2,1)( )
A.在直线l上,但不在曲线上
B.在直线l上,也在曲线上
C.不在直线l上,也不在曲线上
D.不在直线l上,但在曲线上
答案:B
解析:将M(2,1)代入直线方程,2+1-3=0,
将M(2,1)代入曲线方程,(2-3)2+(1-2)2=2,
故点M在l上,也在曲线上.
检
共 12 页
*
3、
检
共 12 页
*
解析:(1)方程 ,表示的曲线是以(2,0)为对称中心,焦点在x轴上,长轴长为6,焦距为 的椭圆.
(2)方程(x+2)2+(y-2)2=16表示的曲线是以(-2,2)为圆心,4为半径的圆.
(3)方程(2x+3y-5) =0表示直线2x+3y-5=0与射线x=4(x≥3).
(4)方程 ,可以看作点(x,y)到(2,0)的距离与到直线x=4的距离之比为2,故此方程表示以(2,0)为焦点,离心率为2的双曲线.
共 12 页
*
4.设动点P在直线x=1上,O为坐标原点,以OP为直角边,以点O为直角顶点作等腰Rt△OPQ,则动点Q的轨迹是( )
A.圆 B.两条平行直线
C.抛物线 D.双曲线
答案:B
坐标法
检
