1.1.3 导数的几何意义 课件(20张PPT)
文档属性
| 名称 | 1.1.3 导数的几何意义 课件(20张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 292.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:16:23 | ||
图片预览






文档简介
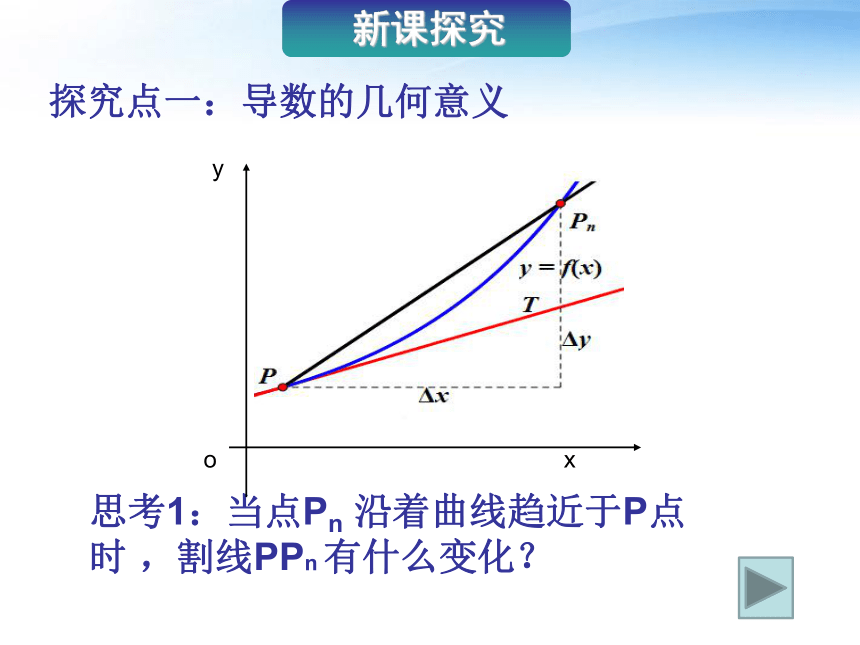
课件20张PPT。1.1.3 导数的几何意义 复习回顾割线的斜率 ?平均速度瞬时速度平均变化率物理意义瞬时变化率/导数 几何意义思考1:当点Pn 沿着曲线趋近于P点时 ,割线PPn 有什么变化? 新课探究探究点一:导数的几何意义P相切相交PPn切线T当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为点P处的切线.思考2:割线与切线的斜率有何关系呢?△x→0,割线PPn →切线PT
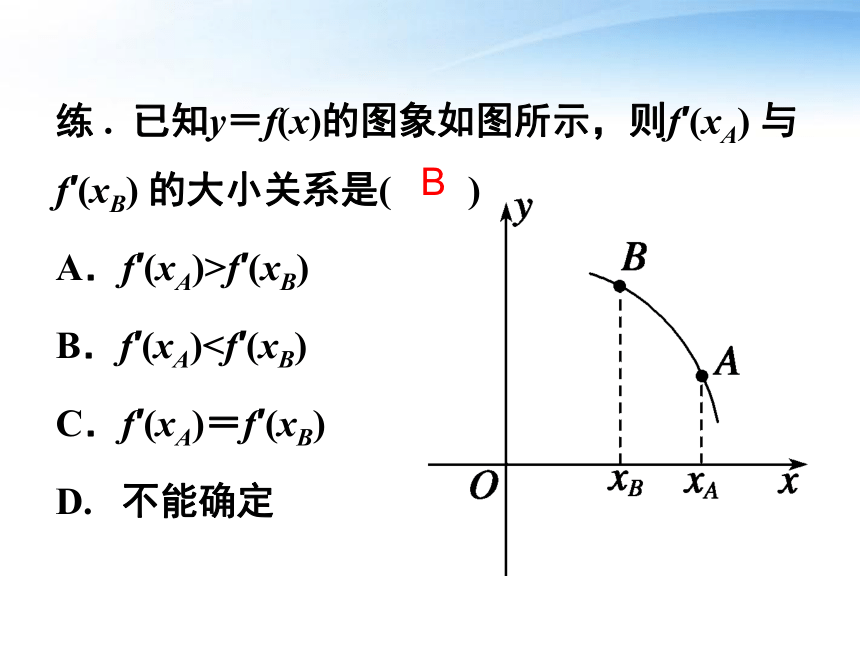
割线PPn的斜率→切线PT的 斜率 函数y=f(x)在x=x0处的导数就是导数的几何意义在该点处切线的斜率练 . 已知y=f(x)的图象如图所示,则f′(xA) 与f′(xB) 的大小关系是( )
A.f′(xA)>f′(xB)
B.f′(xA)C.f′(xA)=f′(xB)
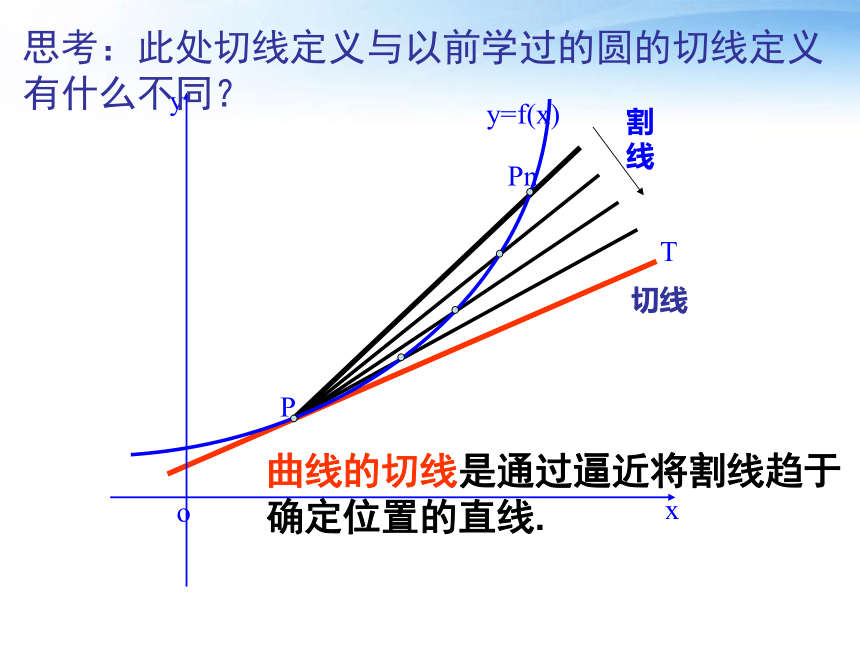
D. 不能确定BPPn切线T曲线的切线是通过逼近将割线趋于确定位置的直线.思考:此处切线定义与以前学过的圆的切线定义有什么不同?思考:不能直线与圆有惟一公共点时,
直线叫做圆的切线。能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。问:直线 , 是曲线的切线吗? 通过逼近的方法,将割线趋于确定位置的直线定义为切线。
这种定义适用于各种曲线。公共点可能不唯一 求抛物线y=x2在点P(1,1)处的切线方程.2x-y-1=0求抛物线y=x2 过点 的切线方程.x+4y-4=0探究点二:求曲线的切线方程求抛物线y=x2 过点 的切线方程.解:设切点为(x0, x02)所以x0=2或3
k=4或6切线方程为:y=4x-4或y=6x-91.如果曲线y=f(x)在点(x0,f(x0))处的切线
方程为x+2y-3=0,那么( )B2.(2011年山东高考)
曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵
坐标是 ( )
A. -9 B.-3 C.9 D. 15
cA3.(2010年全国Ⅱ)若曲线y=x2+ax+b在点(0,b)
处的切线方程是x-y+1=0,则( )
A. a=1,b=1 B. a=-1,b=1
C. a=1,b=-1 D. a=-1,b=-1
我还有哪些问题是感到困惑的? 我学到了哪些数学知识? 作业:练习B.1,2 练习册求曲线y=x3过点P(1,1)的切线方程.思考导数知识建构谢谢大家!
割线PPn的斜率→切线PT的 斜率 函数y=f(x)在x=x0处的导数就是导数的几何意义在该点处切线的斜率练 . 已知y=f(x)的图象如图所示,则f′(xA) 与f′(xB) 的大小关系是( )
A.f′(xA)>f′(xB)
B.f′(xA)
D. 不能确定BPPn切线T曲线的切线是通过逼近将割线趋于确定位置的直线.思考:此处切线定义与以前学过的圆的切线定义有什么不同?思考:不能直线与圆有惟一公共点时,
直线叫做圆的切线。能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。问:直线 , 是曲线的切线吗? 通过逼近的方法,将割线趋于确定位置的直线定义为切线。
这种定义适用于各种曲线。公共点可能不唯一 求抛物线y=x2在点P(1,1)处的切线方程.2x-y-1=0求抛物线y=x2 过点 的切线方程.x+4y-4=0探究点二:求曲线的切线方程求抛物线y=x2 过点 的切线方程.解:设切点为(x0, x02)所以x0=2或3
k=4或6切线方程为:y=4x-4或y=6x-91.如果曲线y=f(x)在点(x0,f(x0))处的切线
方程为x+2y-3=0,那么( )B2.(2011年山东高考)
曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵
坐标是 ( )
A. -9 B.-3 C.9 D. 15
cA3.(2010年全国Ⅱ)若曲线y=x2+ax+b在点(0,b)
处的切线方程是x-y+1=0,则( )
A. a=1,b=1 B. a=-1,b=1
C. a=1,b=-1 D. a=-1,b=-1
我还有哪些问题是感到困惑的? 我学到了哪些数学知识? 作业:练习B.1,2 练习册求曲线y=x3过点P(1,1)的切线方程.思考导数知识建构谢谢大家!
