1.4.2 微积分基本定理 课件(17张PPT)
文档属性
| 名称 | 1.4.2 微积分基本定理 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 326.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:30:25 | ||
图片预览




文档简介
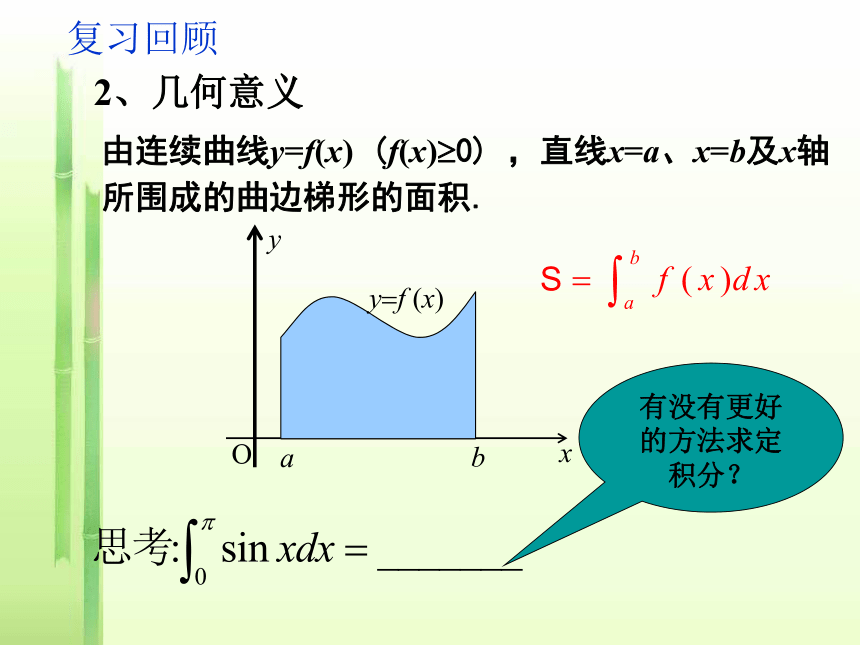
课件17张PPT。 微积分基本定理普通高中课程标准实验教科书——选修2-2公元3世纪诞生的刘徽著名的“割圆术”: 割之弥细,所失越少.则与圆周合体而无所失矣.割之又割,以至于不可割,定积分的定义:1、定义法(分割、近似代替、求和、取极限)复习回顾 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴
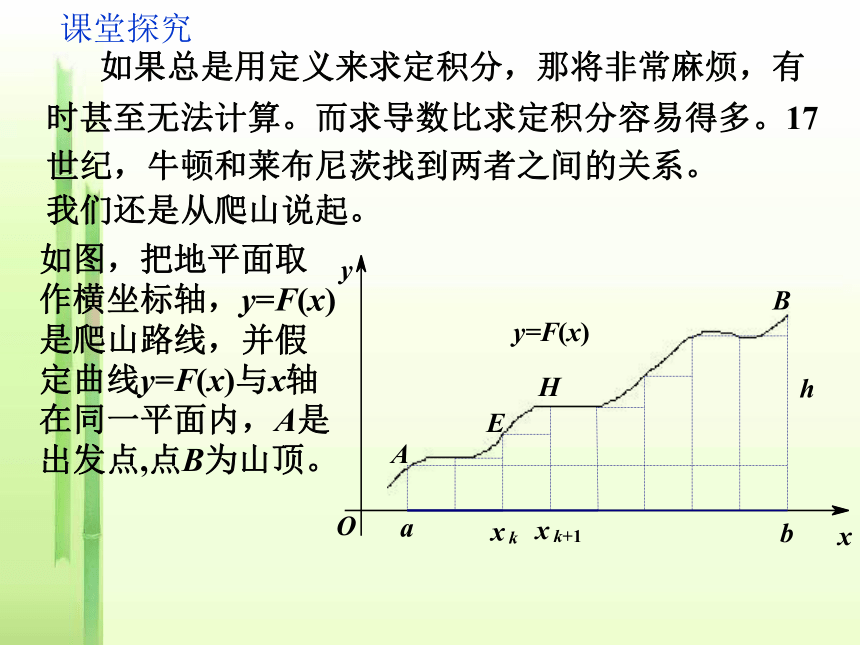
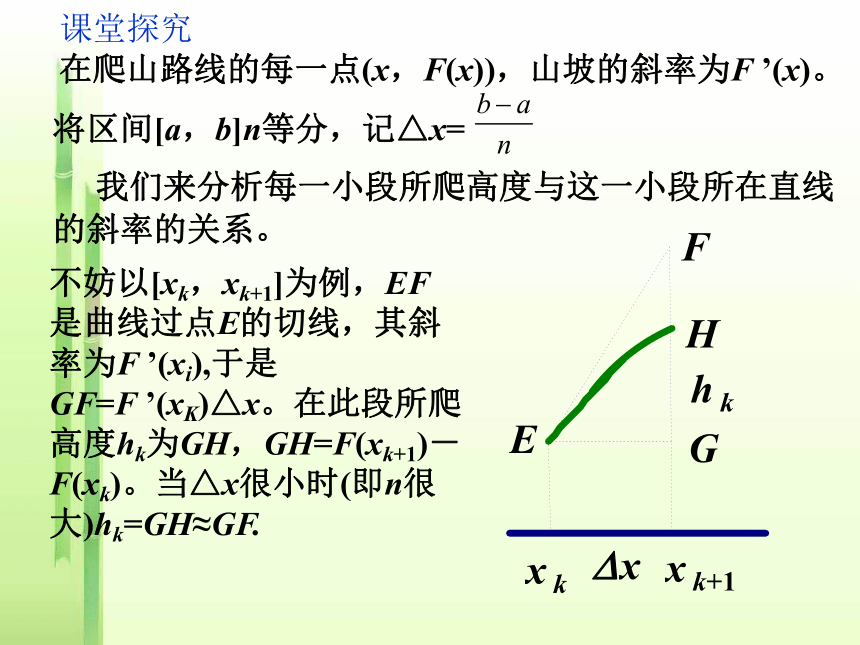
所围成的曲边梯形的面积.2、几何意义复习回顾有没有更好的方法求定积分? 如果总是用定义来求定积分,那将非常麻烦,有时甚至无法计算。而求导数比求定积分容易得多。17世纪,牛顿和莱布尼茨找到两者之间的关系。我们还是从爬山说起。如图,把地平面取作横坐标轴,y=F(x)是爬山路线,并假定曲线y=F(x)与x轴在同一平面内,A是出发点,点B为山顶。课堂探究 我们来分析每一小段所爬高度与这一小段所在直线的斜率的关系。 不妨以[xk,xk+1]为例,EF是曲线过点E的切线,其斜率为F ’(xi),于是GF=F ’(xK)△x。在此段所爬高度hk为GH,GH=F(xk+1)-F(xk)。当△x很小时(即n很大)hk=GH≈GF. 课堂探究即F(xk+1)-F(xk)≈F ’(xk)△x. 这样,我们得到了一系列近似等式:
h1=F(a+△x)-F(a) ≈F ’(a)△x,
h2=F(a+2△x)-F(a+△x)≈F’(a+△x)△x,
h3=F(a+3△x)-F(a+2△x)≈F’(a+2△x)△x,
…………
hn-1=F[a+(n-1)△x]-[(a+(n-2)△x)
≈F ’[a+(n-2))△x]△x,
hn=F(b)-F[a+(n-1)△x)
≈F ’[a+(n-1)△x]△x,课堂探究 将上列n个近似等式相加,得到从A到B所爬的总高度
h=h1+h2+……+hn=F(b)-F(a)由定积分定义可知:当△x→0时, 这一公式告诉我们:F ’(x)从a到b的积分等于F(x)在两端点的取值之差 课堂探究微积分基本定理 如果F ’(x)=f(x),且f(x)在[a,b]上可积,则 其中F(x)叫做f(x)的一个原函数。牛顿—莱布尼茨公式求导数与定积分是互为逆运算课堂新知回顾:基本初等函数的导数公式新知:基本初等函数的原函数公式例1 计算:(1) ;
(2)解:(1)因为所以 (2)因为 所以 课堂练习例2.求曲边图形面积
(1)求y=sinx在[0,π]上阴影部分的面积S.(2)求曲线y=sinx与x轴在区间[0,2π]上所围成阴影部分的面积S。定积分和曲边图形面积的关系课堂互动 1.微积分基本定理是微积分中最重要、最辉煌的成果,它揭示了导数和定积分之间的内在联系,同时它也提供了计算定积分的一种有效办法. 2.寻找满足 F ’(x)=f(x) 的函数F(x),一般运用基本初等函数的求导公式和导数的四则运算法则,从反方向上求出F(x).课堂收获 3.求曲边图形面积是将积分区间进行细化区间段,然后根据图象对各个区间段分别求面积进而求和,在每个区段上被积函数均是由上减下再见
所围成的曲边梯形的面积.2、几何意义复习回顾有没有更好的方法求定积分? 如果总是用定义来求定积分,那将非常麻烦,有时甚至无法计算。而求导数比求定积分容易得多。17世纪,牛顿和莱布尼茨找到两者之间的关系。我们还是从爬山说起。如图,把地平面取作横坐标轴,y=F(x)是爬山路线,并假定曲线y=F(x)与x轴在同一平面内,A是出发点,点B为山顶。课堂探究 我们来分析每一小段所爬高度与这一小段所在直线的斜率的关系。 不妨以[xk,xk+1]为例,EF是曲线过点E的切线,其斜率为F ’(xi),于是GF=F ’(xK)△x。在此段所爬高度hk为GH,GH=F(xk+1)-F(xk)。当△x很小时(即n很大)hk=GH≈GF. 课堂探究即F(xk+1)-F(xk)≈F ’(xk)△x. 这样,我们得到了一系列近似等式:
h1=F(a+△x)-F(a) ≈F ’(a)△x,
h2=F(a+2△x)-F(a+△x)≈F’(a+△x)△x,
h3=F(a+3△x)-F(a+2△x)≈F’(a+2△x)△x,
…………
hn-1=F[a+(n-1)△x]-[(a+(n-2)△x)
≈F ’[a+(n-2))△x]△x,
hn=F(b)-F[a+(n-1)△x)
≈F ’[a+(n-1)△x]△x,课堂探究 将上列n个近似等式相加,得到从A到B所爬的总高度
h=h1+h2+……+hn=F(b)-F(a)由定积分定义可知:当△x→0时, 这一公式告诉我们:F ’(x)从a到b的积分等于F(x)在两端点的取值之差 课堂探究微积分基本定理 如果F ’(x)=f(x),且f(x)在[a,b]上可积,则 其中F(x)叫做f(x)的一个原函数。牛顿—莱布尼茨公式求导数与定积分是互为逆运算课堂新知回顾:基本初等函数的导数公式新知:基本初等函数的原函数公式例1 计算:(1) ;
(2)解:(1)因为所以 (2)因为 所以 课堂练习例2.求曲边图形面积
(1)求y=sinx在[0,π]上阴影部分的面积S.(2)求曲线y=sinx与x轴在区间[0,2π]上所围成阴影部分的面积S。定积分和曲边图形面积的关系课堂互动 1.微积分基本定理是微积分中最重要、最辉煌的成果,它揭示了导数和定积分之间的内在联系,同时它也提供了计算定积分的一种有效办法. 2.寻找满足 F ’(x)=f(x) 的函数F(x),一般运用基本初等函数的求导公式和导数的四则运算法则,从反方向上求出F(x).课堂收获 3.求曲边图形面积是将积分区间进行细化区间段,然后根据图象对各个区间段分别求面积进而求和,在每个区段上被积函数均是由上减下再见
