2.2.2 反证法 课件(29张PPT)
文档属性
| 名称 | 2.2.2 反证法 课件(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览






文档简介
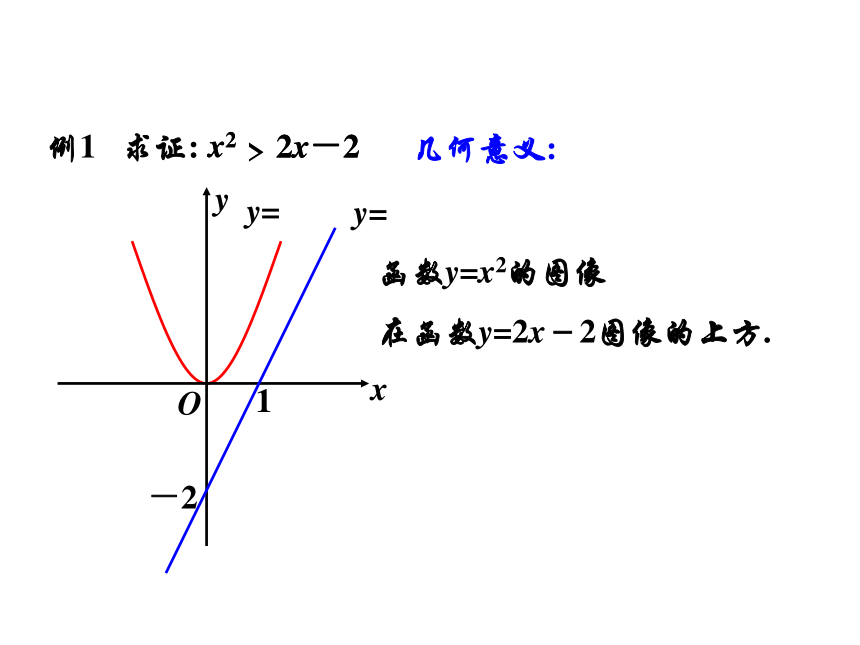
课件29张PPT。为数学打开一扇天窗让学生插上智慧翅膀x2 x2-(2x-2) =x2-2x+2 =x2-2x+1+1 =(x-1)2+1>0∴ x2>2x-2.例1 求证:2x-2与你能比较的大小吗?>不等式证明(1)比较法:差值步骤:①作差②变形③定号关键!(配方、因式分解、通分…)证明:…………….作差…………….变形…………….定号问题:x2>2x-2x2例1 求证:2x-2y=y=函数y=x2的图像
在函数y=2x-2图像的上方.几何意义:例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)a2+ b2- ab- a- b + 1222222=( )≥0证明: ∴a2+b2≥ab+a+b -1.分组配方,变形为平方和结构.证明:=a2b2+5-2ab+a2+4a=(ab-1)2+(a+2)2≥0(a2b2+5) -(2ab-a2-4a)=(a2b2-2ab+(a2+4a+4)+1 ) ∴ a2b2+5≥2ab-a2-4a.练习1. 求证: a2b2+5≥2ab-a2-4a.2.若x, y, z∈R, a, b, c∈R+,求证: ≥2(xy+yz+zx)-2(xy+yz+zx)≥0证明:≥2(xy+yz+zx).-2xy-2yz-2zx练习例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)a2+ b2- ab- a- b + 1222222=( )≥0证明: ∴a2+b2≥ab+a+b -1.≥0证明2:a2+b2≥ab+a+b -1.1:例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)a2+ b2- ab- a- b + 1222222=( )≥0证明: ∴a2+b2≥ab+a+b -1.1:例2 求证: a2+b2≥ab+a+b -1a2+b2≥2aba2+12≥2ab2+12≥2b2a2+2b2+2≥2ab+2a+2b a2+b2≥ab+a+b -1证明3:a2+b2-(ab+a+b -1)=a2+b2-ab-a-b+1相加≥0证明2:a2+b2≥ab+a+b -1.a2+b2 ≥2ab重要不等式:例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)证明=a2+b2-ab-a-b+1=a2-(b+1)a+ (b2-b+1)=a2+b2-ab-a-b+1+ (b2-b+1)≥0 ∴a2+b2≥ab+a+b -1.4:(看着a的二次函数)f(a)=主元思想例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)证明=a2+b2-ab-a-b+1=a2-(b+1)a+ (b2-b+1)=a2+b2-ab-a-b+15:△=-4(b2-b+1) (b+1)2=-3(b-1)2≤0.∴ f(a)≥0,二次项系数是1,函数思想(看着a的二次函数)f(a)= ∴a2+b2≥ab+a+b -1.主元思想= ab2+bc2+ca2 -a2b-b2c -c2a例3 设a>b>c, 求证: ab2+bc2+ca2 < a2b+b2c +c2a.ab2+bc2+ca2 -(a2b+b2c +c2a)= ab(b-a)+bc(c-b)+ca(a-c)--+不行 != ab2+bc2+ca2 -a2b-b2c -c2a= b2(a-c)+c2(b-a)+a2(c-b)--+不行 !a>b>ca-b>0b-c>0a-c>0分析:主元思想,可把零乱的字母归类,然后对式子进行有序管理.= ab2+bc2+ca2 -a2b-b2c -c2a例3 设a>b>c, 求证: ab2+bc2+ca2 < a2b+b2c +c2a.a>b>ca-b>0b-c>0a-c>0ab2+bc2+ca2 -(a2b+b2c +c2a)-++= (c -b)a2+(b-c)(b+c)a = (c -b)1
1-b
-c= (c -b) (a-b) (a -c)<0证明:= ab2+bc2+ca2 -a2b-b2c -c2a+(b2-c2)a +bc(c-b)[a2∴ ab2+bc2+ca2 < a2b+b2c +c2a.因式分解(或变形)
为积(或商)的形式,
且符号可定.f(a)== (c -b)a2+bc(c-b)以 a 为主变元-(b+c)a+bc]= ab2+bc2+ca2 -a2b-b2c -c2a例3 设a>b>c, 求证: ab2+bc2+ca2 < a2b+b2c +c2a.a>b>ca-b>0b-c>0a-c>0证明:c-b<0,ab2+bc2+ca2 -(a2b+b2c +c2a)f(a)=二次项系数:△=-4bc(c-b)2 (b2-c2)2 =(b-c)4= (c -b)a2+(b2-c2)a +bc(c-b)看着a的二次函数>0.∴ f(a)<0, 即 ab2+bc2+ca2 < a2b+b2c +c2a.以 a 为主变元学生完成bc∵ a>b,?并非一定要求整个函数图像都在x轴的下方3. 设a, b, c∈[0, 2],证明: 4a+b2+c2+abc≥2ab+2bc+2ca.a f(a)==(b-c)2=(b-2)2+(c-2)24a+b2+c2+abc≥2ab+2bc+2ca.练习(4a+b2+c2+abc)-(2ab+2bc+2ca)≥0≥0f(a)≥0证明:f(a)aaaa=(4+bc-2b-2c)+b2+c2-2bc以 a 为主变元:f(0)=f(2)=b2+c2-2bcb2+c2-4b-4c+8小结(差值)比较法函数平方和式子的积商(关键!)方法配方因式分解通分…结果①作差②变形③定号步骤:主元思想函数思想思想: 本节课到此结束, 请同学们课后再做好复习与作业。谢谢!再见!Homework: 见后3. 已知a, b, m都是正数, 并且a < b, 求证:4.已知a, b都是正数, 并且a ? b, 求证:a5 + b5 > a2b3 + a3b22. 求证: x2 + 3 > 3x6.己知函数f(x)=x2+ax+b, 非负实数p, q满足p+q=1,
证明: pf(x)+qf(y)≥f(px+qy).5.已知a, b, c为正实数, 且a+b+c=1.求证: a2+b2+c2≥1.已知1A MN D M与N大小不确定作业证明:5.已知a, b, c为正实数, 且a+b+c=1.求证: a2+b2+c2≥(3a2+3b2+3c2-1)a2+b2+c2-[3a2+3b2+3c2=-a2-b2-c2-2ab-2ac-2bc]-(a+b+c)2]==[(a-b)2+(b-c)2+(c-a)2][3a2+3b2+3c2=≥0∴a2+b2+c2≥解答:小结(差值)比较法综合法分析法一题多解多题一解二次函数平方和式子的积商关键!举三反一是为了举一反三直接法间接法方法配方因式分解通分…结果①作差②变形③定号不管内容, 不论成败, 只作平台, 给同仁们提供一个交流探讨的机会, 所以献丑了, 占用了大家的宝贵时间.题中变量:从例1的一个增加到例3的三个;解题方法: 从最基本的配方、因式分解到主元思想、函数思想.关于层次感近年来, 对习题课的类型教学有些不同看法, 在应试教育下, 为数众多的老师热衷于给学生讲习题类型, 但是, 常常只是“罗列式”, 没有归纳、总结、升华, 或者归纳总结升华得不十分得法、到位; 另一种相反的观点是, 课改之后要淡化类型.关于“类型”我认为:
第一: 类型是认识过程中的重要中介产品, 心理学上叫图式, 专家和新手之间的重要差别之一就是P133议应该说这节课条理清晰,让同学可以形成一定的认知结构.现在有为数不少的老师,在选择例题时是拉在篮里便是菜..笔者曾经听过一节课,这位老师在一系列例题中突然夹了一个和主题不相干的题目,事后我问她这道题,你的意图是什么?她回答说我在做题目的时候觉得这道题蛮好的,我就加进去了.相比这种情况,老师对例题的选择是有思考的,例题有一定的典型性,难度也适当.但是老师过于强调模仿,下面的话,老师在课堂上说过两遍以后遇到这样的类型就不怕了.这样的话,我关于层次感这样的话,我在其他老师嘴里也经常听到.看来,老师企图依靠把典型题目让大家做个遍,来达到提高质量的目的,这样恐怕免不了还是要走进题海的路子,我们常常说,为了让学生跳出题海,老师首先要跳进题海,老师跳进题海做什么?是要去芜存精,还要理岀头绪.去芜存精就是要选择典型的题目.理岀头绪则是要根据数学内在的结构和学生的认识规律.安排出乛个题目的屋次.这是两件很见功力的事情.这节课的选题还是可以的,可以改进的地方,主要就是应该根据数学的结构和学生的认知规律安排一个合理的层次,首先,老师指出今天的求值和过去的求值不同,那就是过去求值是已知x.Y的值,求关于xY的代数式的值.关于层次感今天的己知条件不那么具体,而只是知道了某个关于xY的条件.学生固然可以意会两者的差别,如果点明今天讲的是条件求值,以有别于以前学过的简单求值题是大有益,因为这有利于学生形成更好的认知结构.第二,点明条件求值的主题后,怎么么办?不应该急着就事论事地解这道题,而应该是组织大家思考能不能转化为普通求值.这样的思考,符合化未知为己知的化归思想,有利于学生的认识水平的提高.因此,把能够求出xY的值的例1(2)提前比较合适,因为它是化为简单求值题解决.这个次序上的调整,符合了这类问题的数学结构和认知规律.如果这样选择,安排和讲解例题不需要做很多的题目,不需要机械的模仿,学生可以容易地掌握这方面的知识技能,而且对各种方法的来龙去脉乛为什么要用这种方法?怎么想到用这种方法的?怎样用这种方法?乛比较清晰,不但知其然,亅而且知其所以然了,关于层次感也就是说可以帮助学生形成良好的认知结构.而要做到这样的安排,关键在于教师对数学的理解.正因为,老师对这段数学知识理解上还不够深刻,所以她的这节习题课,尽管比拉在篮里便是菜式习题课好得多,但还没有完全跳出罗列十模仿的框框..教师对数学的理解深不深,或者说数学功底好不好,这话不容易讲清楚,陈景润是大数学家,但做不好老师,我认识有位老师,在上级的解数学题的测试中表现良好,但就是教不好书面临换岗的局面.所以,对数学理解深刻,未必就是求学时数学成绩好,或者会做数学题.关于层次感张奠宙教授说数学有三种形态,原始形态,学术形态和教育形态.原始形态是数学家创造时的数学,弯弯曲曲的,学术形态则是数学家表达自己成果的形态,板起面孔的,而教育形态则是用学生容易接受的方式整理的.又是有利于学生发展的形态.我想,我们通常所说的教师对数学理解,本质上是对数学的教育形态掌握得比较好,运用得比较得当,这就要求我们研究每章每节的双基要求和结构,重点难点,以及学生容易造成错误的地方. P121: 目前,大多数老师奉行的是题海战术.弄得学生很累很苦,而且还是摸不着头脑,而W老师认真钻研了相关的内容,她肯定做了很多的题目,把这些题目理出了思路,不等式证明有多种方法,第一种是比较法,比较法的关键是变形,而变形又常用三种方法!变形为完全平方的和,变形为某些式子的积(或商) (这些式子的符号可定).把它作为一次或二次函数来处理。这显出了W老师的数学功底是很好的.根据这些,W老师选择的例题就很有典型性了.典型的题目,应该是反映这类问题的本质,,而且最好有多种解法.运用一题多解可激发学生的兴趣,活跃了学生的思维。而且一题多解,不完全是技巧视野比较宽?譬如例l的几何解释,例2的证明3和涉及了主元思想.如果大家都像W老师那样.例题讲究典型性,又有方法的归纳,关键点的点拨,又进行一题多解培养思维的灵活性,还需要题海战术吗?有句话叫为了让学生跳出题海,要求我们教师先跳进题海,其实先跳进题海是第一步跳进去了还要思考整理.关于这节课不要一个人讲,而是调动学生的思维,大家一起来思考讨论,有些老师为活跃而活跃,其实学生课堂的活跃不活跃,不是看形式,而是看思维的状态。老师有放有收,在指导下放,活跃
老师的劳动是创
在函数y=2x-2图像的上方.几何意义:例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)a2+ b2- ab- a- b + 1222222=( )≥0证明: ∴a2+b2≥ab+a+b -1.分组配方,变形为平方和结构.证明:=a2b2+5-2ab+a2+4a=(ab-1)2+(a+2)2≥0(a2b2+5) -(2ab-a2-4a)=(a2b2-2ab+(a2+4a+4)+1 ) ∴ a2b2+5≥2ab-a2-4a.练习1. 求证: a2b2+5≥2ab-a2-4a.2.若x, y, z∈R, a, b, c∈R+,求证: ≥2(xy+yz+zx)-2(xy+yz+zx)≥0证明:≥2(xy+yz+zx).-2xy-2yz-2zx练习例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)a2+ b2- ab- a- b + 1222222=( )≥0证明: ∴a2+b2≥ab+a+b -1.≥0证明2:a2+b2≥ab+a+b -1.1:例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)a2+ b2- ab- a- b + 1222222=( )≥0证明: ∴a2+b2≥ab+a+b -1.1:例2 求证: a2+b2≥ab+a+b -1a2+b2≥2aba2+12≥2ab2+12≥2b2a2+2b2+2≥2ab+2a+2b a2+b2≥ab+a+b -1证明3:a2+b2-(ab+a+b -1)=a2+b2-ab-a-b+1相加≥0证明2:a2+b2≥ab+a+b -1.a2+b2 ≥2ab重要不等式:例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)证明=a2+b2-ab-a-b+1=a2-(b+1)a+ (b2-b+1)=a2+b2-ab-a-b+1+ (b2-b+1)≥0 ∴a2+b2≥ab+a+b -1.4:(看着a的二次函数)f(a)=主元思想例2 求证: a2+b2≥ab+a+b -1a2+b2-(ab+a+b -1)证明=a2+b2-ab-a-b+1=a2-(b+1)a+ (b2-b+1)=a2+b2-ab-a-b+15:△=-4(b2-b+1) (b+1)2=-3(b-1)2≤0.∴ f(a)≥0,二次项系数是1,函数思想(看着a的二次函数)f(a)= ∴a2+b2≥ab+a+b -1.主元思想= ab2+bc2+ca2 -a2b-b2c -c2a例3 设a>b>c, 求证: ab2+bc2+ca2 < a2b+b2c +c2a.ab2+bc2+ca2 -(a2b+b2c +c2a)= ab(b-a)+bc(c-b)+ca(a-c)--+不行 != ab2+bc2+ca2 -a2b-b2c -c2a= b2(a-c)+c2(b-a)+a2(c-b)--+不行 !a>b>ca-b>0b-c>0a-c>0分析:主元思想,可把零乱的字母归类,然后对式子进行有序管理.= ab2+bc2+ca2 -a2b-b2c -c2a例3 设a>b>c, 求证: ab2+bc2+ca2 < a2b+b2c +c2a.a>b>ca-b>0b-c>0a-c>0ab2+bc2+ca2 -(a2b+b2c +c2a)-++= (c -b)a2+(b-c)(b+c)a = (c -b)1
1-b
-c= (c -b) (a-b) (a -c)<0证明:= ab2+bc2+ca2 -a2b-b2c -c2a+(b2-c2)a +bc(c-b)[a2∴ ab2+bc2+ca2 < a2b+b2c +c2a.因式分解(或变形)
为积(或商)的形式,
且符号可定.f(a)== (c -b)a2+bc(c-b)以 a 为主变元-(b+c)a+bc]= ab2+bc2+ca2 -a2b-b2c -c2a例3 设a>b>c, 求证: ab2+bc2+ca2 < a2b+b2c +c2a.a>b>ca-b>0b-c>0a-c>0证明:c-b<0,ab2+bc2+ca2 -(a2b+b2c +c2a)f(a)=二次项系数:△=-4bc(c-b)2 (b2-c2)2 =(b-c)4= (c -b)a2+(b2-c2)a +bc(c-b)看着a的二次函数>0.∴ f(a)<0, 即 ab2+bc2+ca2 < a2b+b2c +c2a.以 a 为主变元学生完成bc∵ a>b,?并非一定要求整个函数图像都在x轴的下方3. 设a, b, c∈[0, 2],证明: 4a+b2+c2+abc≥2ab+2bc+2ca.a f(a)==(b-c)2=(b-2)2+(c-2)24a+b2+c2+abc≥2ab+2bc+2ca.练习(4a+b2+c2+abc)-(2ab+2bc+2ca)≥0≥0f(a)≥0证明:f(a)aaaa=(4+bc-2b-2c)+b2+c2-2bc以 a 为主变元:f(0)=f(2)=b2+c2-2bcb2+c2-4b-4c+8小结(差值)比较法函数平方和式子的积商(关键!)方法配方因式分解通分…结果①作差②变形③定号步骤:主元思想函数思想思想: 本节课到此结束, 请同学们课后再做好复习与作业。谢谢!再见!Homework: 见后3. 已知a, b, m都是正数, 并且a < b, 求证:4.已知a, b都是正数, 并且a ? b, 求证:a5 + b5 > a2b3 + a3b22. 求证: x2 + 3 > 3x6.己知函数f(x)=x2+ax+b, 非负实数p, q满足p+q=1,
证明: pf(x)+qf(y)≥f(px+qy).5.已知a, b, c为正实数, 且a+b+c=1.求证: a2+b2+c2≥1.已知1
第一: 类型是认识过程中的重要中介产品, 心理学上叫图式, 专家和新手之间的重要差别之一就是P133议应该说这节课条理清晰,让同学可以形成一定的认知结构.现在有为数不少的老师,在选择例题时是拉在篮里便是菜..笔者曾经听过一节课,这位老师在一系列例题中突然夹了一个和主题不相干的题目,事后我问她这道题,你的意图是什么?她回答说我在做题目的时候觉得这道题蛮好的,我就加进去了.相比这种情况,老师对例题的选择是有思考的,例题有一定的典型性,难度也适当.但是老师过于强调模仿,下面的话,老师在课堂上说过两遍以后遇到这样的类型就不怕了.这样的话,我关于层次感这样的话,我在其他老师嘴里也经常听到.看来,老师企图依靠把典型题目让大家做个遍,来达到提高质量的目的,这样恐怕免不了还是要走进题海的路子,我们常常说,为了让学生跳出题海,老师首先要跳进题海,老师跳进题海做什么?是要去芜存精,还要理岀头绪.去芜存精就是要选择典型的题目.理岀头绪则是要根据数学内在的结构和学生的认识规律.安排出乛个题目的屋次.这是两件很见功力的事情.这节课的选题还是可以的,可以改进的地方,主要就是应该根据数学的结构和学生的认知规律安排一个合理的层次,首先,老师指出今天的求值和过去的求值不同,那就是过去求值是已知x.Y的值,求关于xY的代数式的值.关于层次感今天的己知条件不那么具体,而只是知道了某个关于xY的条件.学生固然可以意会两者的差别,如果点明今天讲的是条件求值,以有别于以前学过的简单求值题是大有益,因为这有利于学生形成更好的认知结构.第二,点明条件求值的主题后,怎么么办?不应该急着就事论事地解这道题,而应该是组织大家思考能不能转化为普通求值.这样的思考,符合化未知为己知的化归思想,有利于学生的认识水平的提高.因此,把能够求出xY的值的例1(2)提前比较合适,因为它是化为简单求值题解决.这个次序上的调整,符合了这类问题的数学结构和认知规律.如果这样选择,安排和讲解例题不需要做很多的题目,不需要机械的模仿,学生可以容易地掌握这方面的知识技能,而且对各种方法的来龙去脉乛为什么要用这种方法?怎么想到用这种方法的?怎样用这种方法?乛比较清晰,不但知其然,亅而且知其所以然了,关于层次感也就是说可以帮助学生形成良好的认知结构.而要做到这样的安排,关键在于教师对数学的理解.正因为,老师对这段数学知识理解上还不够深刻,所以她的这节习题课,尽管比拉在篮里便是菜式习题课好得多,但还没有完全跳出罗列十模仿的框框..教师对数学的理解深不深,或者说数学功底好不好,这话不容易讲清楚,陈景润是大数学家,但做不好老师,我认识有位老师,在上级的解数学题的测试中表现良好,但就是教不好书面临换岗的局面.所以,对数学理解深刻,未必就是求学时数学成绩好,或者会做数学题.关于层次感张奠宙教授说数学有三种形态,原始形态,学术形态和教育形态.原始形态是数学家创造时的数学,弯弯曲曲的,学术形态则是数学家表达自己成果的形态,板起面孔的,而教育形态则是用学生容易接受的方式整理的.又是有利于学生发展的形态.我想,我们通常所说的教师对数学理解,本质上是对数学的教育形态掌握得比较好,运用得比较得当,这就要求我们研究每章每节的双基要求和结构,重点难点,以及学生容易造成错误的地方. P121: 目前,大多数老师奉行的是题海战术.弄得学生很累很苦,而且还是摸不着头脑,而W老师认真钻研了相关的内容,她肯定做了很多的题目,把这些题目理出了思路,不等式证明有多种方法,第一种是比较法,比较法的关键是变形,而变形又常用三种方法!变形为完全平方的和,变形为某些式子的积(或商) (这些式子的符号可定).把它作为一次或二次函数来处理。这显出了W老师的数学功底是很好的.根据这些,W老师选择的例题就很有典型性了.典型的题目,应该是反映这类问题的本质,,而且最好有多种解法.运用一题多解可激发学生的兴趣,活跃了学生的思维。而且一题多解,不完全是技巧视野比较宽?譬如例l的几何解释,例2的证明3和涉及了主元思想.如果大家都像W老师那样.例题讲究典型性,又有方法的归纳,关键点的点拨,又进行一题多解培养思维的灵活性,还需要题海战术吗?有句话叫为了让学生跳出题海,要求我们教师先跳进题海,其实先跳进题海是第一步跳进去了还要思考整理.关于这节课不要一个人讲,而是调动学生的思维,大家一起来思考讨论,有些老师为活跃而活跃,其实学生课堂的活跃不活跃,不是看形式,而是看思维的状态。老师有放有收,在指导下放,活跃
老师的劳动是创
