1.3.1 利用导数判断函数的单调性 课件(21张PPT)
文档属性
| 名称 | 1.3.1 利用导数判断函数的单调性 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 387.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:21:29 | ||
图片预览







文档简介
课件21张PPT。 导数在研究函数中的应用
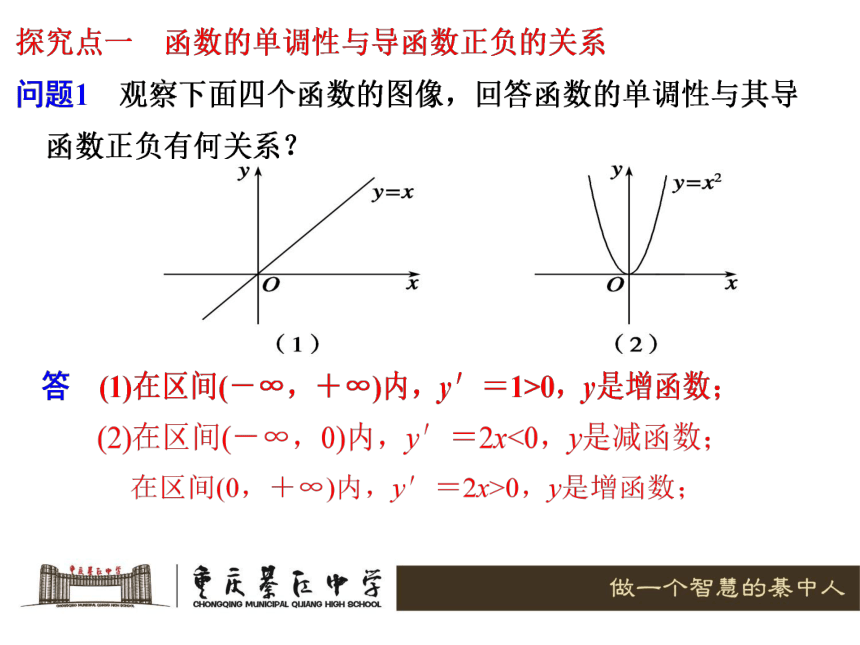
3.1.1 函数的单调性与导数一般地,可导函数在区间(a,b)内的单调性与导数有如下关系: 增 减 通过刚才的观察:你认为可导函数在区间(a,b)内的单调性与导数有什么关系?
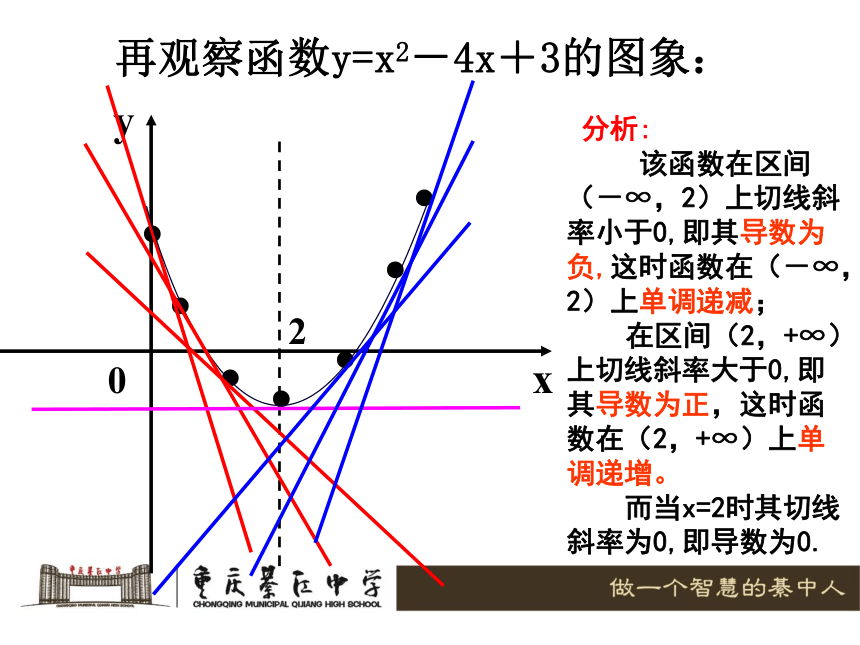
2.......再观察函数y=x2-4x+3的图象: 分析:
该函数在区间
(-∞,2)上切线斜率小于0,即其导数为负,这时函数在(-∞,2)上单调递减;
在区间(2,+∞)上切线斜率大于0,即其导数为正,这时函数在(2,+∞)上单调递增。
而当x=2时其切线斜率为0,即导数为0.这表明:导数的正、负与函数的单调性密
切相关提示:不一定成立.例如y=x3在R上是增函数,但其在x=0处的导数为零,故f′(x)>0是y=f(x)在某区间上是增函数的
条件.充分不必要(1)确定函数f(x)的定义域.(2)求出函数的导函数.(3)解不等式f′(x)>0,得函数单增区间;
解不等式f′(x)<0,得函数单减区间. 阅读例2将(3)、(4)补充完整,并小结利用导数求解函数单调区间的步骤。函数增减快慢与导数值大小的关系:
一般地,设函数y=f(x),在区间(a,b)上
(1)如果|f′(x)|越大,函数在区间(a,b)上变化得_____,函
数的图象就比较“陡峭”(向上或向下).
(2)如果|f′(x)|越小,函数在区间(a,b)上变化得_____,函
数的图象就比较“平缓”(向上或向下).越快越慢 阅读例3思考函数增减快慢与导数值大小的关系?
【典例】1.函数 的单调递减区间为( )
A.(-1,1] B.(0,1)
C.[1,+∞) D.(0,+∞)
【解析】选B.由
?0区间为(0,1).
【典型例题】2.设f′(x)是函数f(x)的导数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是选项中的( )小结
1.对函数的单调性与其导数正负的关系的三点说明
(1)利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是函数f(x)在某个区间上递增(或递减)的充分不必要条件.(2)在区间(a,b)内可导的函数f(x)在区间(a,b)上递增(或递减)的充要条件应是f′(x)≥0(或f′(x)≤0)(x∈(a,b))恒成立且f′(x)在区间(a,b)的任意子区间内都不恒等于0.
(3)特别地,如果f′(x)=0,那么函数y=f(x)在这个区间内是常数函数.2.利用导数研究函数单调性时应注意的三个问题
(1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域,解决问题的过程只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(3)如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开. 作业:活页白本62页
3.1.1 函数的单调性与导数一般地,可导函数在区间(a,b)内的单调性与导数有如下关系: 增 减 通过刚才的观察:你认为可导函数在区间(a,b)内的单调性与导数有什么关系?
2.......再观察函数y=x2-4x+3的图象: 分析:
该函数在区间
(-∞,2)上切线斜率小于0,即其导数为负,这时函数在(-∞,2)上单调递减;
在区间(2,+∞)上切线斜率大于0,即其导数为正,这时函数在(2,+∞)上单调递增。
而当x=2时其切线斜率为0,即导数为0.这表明:导数的正、负与函数的单调性密
切相关提示:不一定成立.例如y=x3在R上是增函数,但其在x=0处的导数为零,故f′(x)>0是y=f(x)在某区间上是增函数的
条件.充分不必要(1)确定函数f(x)的定义域.(2)求出函数的导函数.(3)解不等式f′(x)>0,得函数单增区间;
解不等式f′(x)<0,得函数单减区间. 阅读例2将(3)、(4)补充完整,并小结利用导数求解函数单调区间的步骤。函数增减快慢与导数值大小的关系:
一般地,设函数y=f(x),在区间(a,b)上
(1)如果|f′(x)|越大,函数在区间(a,b)上变化得_____,函
数的图象就比较“陡峭”(向上或向下).
(2)如果|f′(x)|越小,函数在区间(a,b)上变化得_____,函
数的图象就比较“平缓”(向上或向下).越快越慢 阅读例3思考函数增减快慢与导数值大小的关系?
【典例】1.函数 的单调递减区间为( )
A.(-1,1] B.(0,1)
C.[1,+∞) D.(0,+∞)
【解析】选B.由
?0
【典型例题】2.设f′(x)是函数f(x)的导数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是选项中的( )小结
1.对函数的单调性与其导数正负的关系的三点说明
(1)利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是函数f(x)在某个区间上递增(或递减)的充分不必要条件.(2)在区间(a,b)内可导的函数f(x)在区间(a,b)上递增(或递减)的充要条件应是f′(x)≥0(或f′(x)≤0)(x∈(a,b))恒成立且f′(x)在区间(a,b)的任意子区间内都不恒等于0.
(3)特别地,如果f′(x)=0,那么函数y=f(x)在这个区间内是常数函数.2.利用导数研究函数单调性时应注意的三个问题
(1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域,解决问题的过程只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(3)如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开. 作业:活页白本62页
