3.1.2 复数的概念
图片预览






文档简介
(共19张PPT)
3.1.2 复数的概念
选修2-2第三章复数
学习目标:
(1)理解复数的基本概念
(2)理解复数相等的充要条件
(3)了解复数的代数表示方法。
学习重点:
引进虚数单位i的必要性、对i的规定、复数的有关概念
学习难点:
实数系扩充到复数系的过程的理解,复数概念的理解
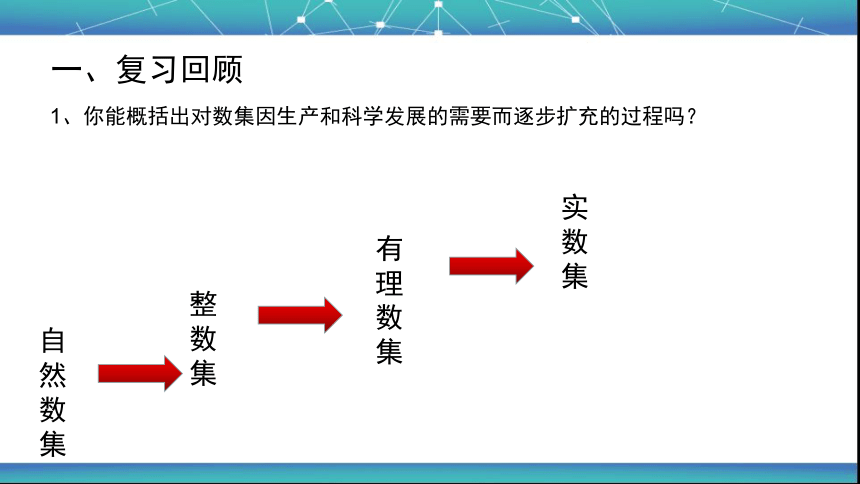
一、复习回顾
1、你能概括出对数集因生产和科学发展的需要而逐步扩充的过程吗?
自然数集
整数集
有
理
数
集
实数集
2、问题:对于实系数一元二次方程 ,
当 时,没有实数根.
我们能否将实数集进行扩充,
使得在新的数集中,
该问题能得到圆满解决呢?
3、引入虚数i
我们引入一个新数i ,i 叫做虚数单位,并规定:
(1)
(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立.
根据前面规定,-1可以开平方,而且-1的平方根是
解决问题:一元二次方程 总有两个根:
新知梳理一
1、复数的概念:
2、复数的代数形式:
3、复数集的表示方法:
练一练:
1.下列数中,( )是实数,( )是虚数, ( ) 是纯虚数?
分别指出这些复数的实部与虚部各是什么?
① ② ③ ④ 0
⑤ ⑥ ⑦ ⑧
①②④⑤
③⑥⑦⑧
③ ⑥
2、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi为虚数
(2)若b为实数,则z=bi必为纯虚数
(3)若a为实数,则z= a一定不是虚数
三、例题讲练
例1 实数m分别取什么值时,
复数z=m+1+(m-1)i是
(1)实数?
(2)虚数?
(3)纯虚数?
总结:确定复数z=a+bi是实数、虚数、纯虚数的条件?
学生练习:
实数m分别取什么值时,
复数 是
(1)实数?(2)虚数?(3)纯虚数?
新知梳理二:
两个复数相等,即两个复数相等的充要条件是它们的实部与虚部分别对应相等。
例2已知 ,其中 ,x,y R,求x与y.
四、思考与小结:
⑴复数集C和实数集R之间有什么关系?___________________
⑵如何对复数a+bi(a,b∈R)进行分类?____________________
⑶复数集、实数集、虚数集、纯虚数集之间的关系,可以用韦恩图表示出来吗?
五、反馈训练、巩固落实
(1)若x,y为实数,且 ,求 与 .
(2)若 ,求 的值.
(3)(2005年湖南卷)复数 的值是( )
A. -1 B. 0 C. 1 D. i
六、作业布置:
课本85页A1,2,3题
3.1.2 复数的概念
选修2-2第三章复数
学习目标:
(1)理解复数的基本概念
(2)理解复数相等的充要条件
(3)了解复数的代数表示方法。
学习重点:
引进虚数单位i的必要性、对i的规定、复数的有关概念
学习难点:
实数系扩充到复数系的过程的理解,复数概念的理解
一、复习回顾
1、你能概括出对数集因生产和科学发展的需要而逐步扩充的过程吗?
自然数集
整数集
有
理
数
集
实数集
2、问题:对于实系数一元二次方程 ,
当 时,没有实数根.
我们能否将实数集进行扩充,
使得在新的数集中,
该问题能得到圆满解决呢?
3、引入虚数i
我们引入一个新数i ,i 叫做虚数单位,并规定:
(1)
(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立.
根据前面规定,-1可以开平方,而且-1的平方根是
解决问题:一元二次方程 总有两个根:
新知梳理一
1、复数的概念:
2、复数的代数形式:
3、复数集的表示方法:
练一练:
1.下列数中,( )是实数,( )是虚数, ( ) 是纯虚数?
分别指出这些复数的实部与虚部各是什么?
① ② ③ ④ 0
⑤ ⑥ ⑦ ⑧
①②④⑤
③⑥⑦⑧
③ ⑥
2、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi为虚数
(2)若b为实数,则z=bi必为纯虚数
(3)若a为实数,则z= a一定不是虚数
三、例题讲练
例1 实数m分别取什么值时,
复数z=m+1+(m-1)i是
(1)实数?
(2)虚数?
(3)纯虚数?
总结:确定复数z=a+bi是实数、虚数、纯虚数的条件?
学生练习:
实数m分别取什么值时,
复数 是
(1)实数?(2)虚数?(3)纯虚数?
新知梳理二:
两个复数相等,即两个复数相等的充要条件是它们的实部与虚部分别对应相等。
例2已知 ,其中 ,x,y R,求x与y.
四、思考与小结:
⑴复数集C和实数集R之间有什么关系?___________________
⑵如何对复数a+bi(a,b∈R)进行分类?____________________
⑶复数集、实数集、虚数集、纯虚数集之间的关系,可以用韦恩图表示出来吗?
五、反馈训练、巩固落实
(1)若x,y为实数,且 ,求 与 .
(2)若 ,求 的值.
(3)(2005年湖南卷)复数 的值是( )
A. -1 B. 0 C. 1 D. i
六、作业布置:
课本85页A1,2,3题
