2.3 数学归纳法(通用) 课件(49张PPT)
文档属性
| 名称 | 2.3 数学归纳法(通用) 课件(49张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 672.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:33:37 | ||
图片预览










文档简介
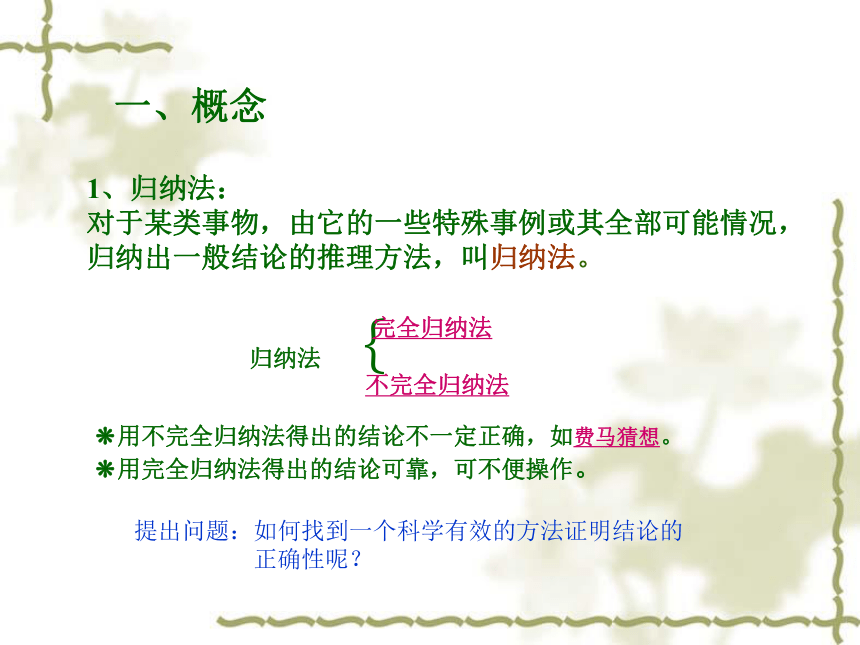
课件49张PPT。数学归纳法一、概念1、归纳法:
对于某类事物,由它的一些特殊事例或其全部可能情况,
归纳出一般结论的推理方法,叫归纳法。?用不完全归纳法得出的结论不一定正确,如费马猜想。
?用完全归纳法得出的结论可靠,可不便操作。提出问题:如何找到一个科学有效的方法证明结论的
正确性呢?如何保证骨牌一一倒下? 需要几个步骤才能到?(1)处理第一个问题;(相当于推倒第一块骨牌)
(2)验证前一问题与后一问题有递推关系;
(相当于前牌推倒后牌)多米诺骨牌课件演示
数学归纳法的定义设{pn}是一个与自然数相关的命题集合,如果(1)证明起始命题p1(或p0)成立;
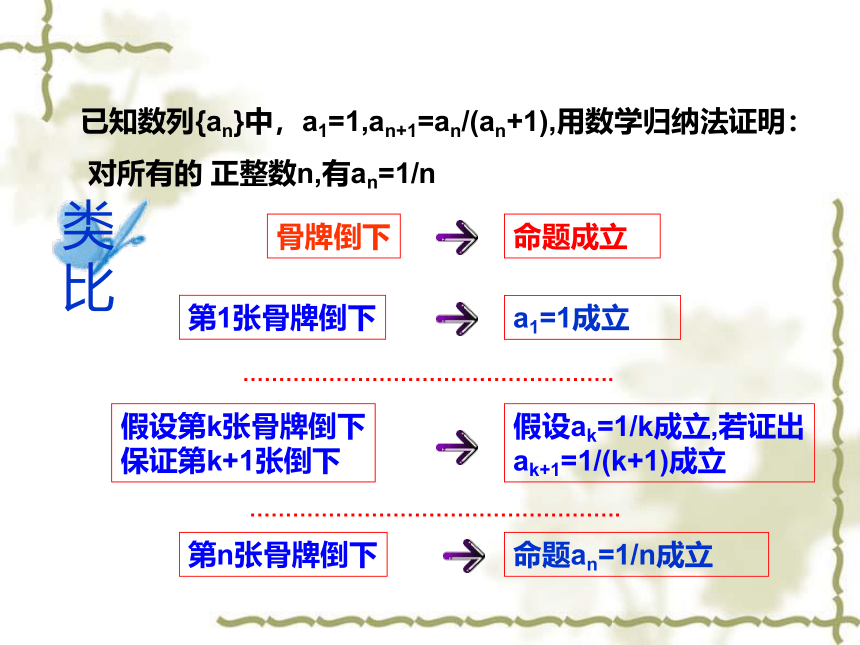
(2)在假设pk成立的前提下,推出pk+1也成立,那么可以断定。{pn}对一切正整数(或自然数)成立,这种方法叫做数学归纳法。 已知数列{an}中,a1=1,an+1=an/(an+1),用数学归纳法证明:
对所有的 正整数n,有an=1/na1=1成立假设ak=1/k成立,若证出
ak+1=1/(k+1)成立命题an=1/n成立命题成立类比 数学归纳法
证明一个与正整数n有关的命题,可按下列步骤:
1.(归纳奠基)证明当n取 时命题成立;2.(归纳递推)假设n=k(k≥n0,k∈N*)时命题成立,证明当
时命题也成立.
只要完成这两个步骤,就可以断定命题对从n0开始的所
有正整数n都成立.第一个值n0(n0∈N*)n=k+1答案: B 解析 :∵n为偶数故假设n=k成立后,再证n=k+2时等式成立.答案: D2.用数学归纳法证明“1+2+22+…+2n+2=2n+3-
1”,在验证n=1时,左边计算所得的式子为 ( )
A.1 B.1+2
C.1+2+22 D.1+2+22+23解析:由n=1时,左=1+2+22+23.答案: D答案:2k答案: 3解析:第一步检验的第一个值n0应为3. 数学归纳法的应用
(1)数学归纳法是一种只适用于与正整数有关的命题的证
明方法,它们的表述严格而且规范,两个步骤缺一不可.第一步是递推的基础,第二步是递推的依据,第二步中,归纳假设起着“已知条件”的作用,在n=k+1时一定要运用它,否则就不是数学归纳法.第二步的关键是“一凑假设,二凑结论”.
(2)在用数学归纳法证明问题的过程中,要注意从k到k+1
时命题中的项与项数的变化,防止对项数估算错误.[例1] 求证:(n+1)(n+2)·…·(n+n)=2n·1·3·5·…·(2n-1)(n∈N*).[自主解答] 当n=1时,等式左边=2,右边=2,故等式成立;假设当n=k时等式成立,
即(k+1)(k+2)·…·(k+k)=2k·1·3·5·…·(2k-1),
那么当n=k+1时,
左边=(k+1+1)(k+1+2)·…·(k+1+k+1)
=(k+2)(k+3)·…·(k+k)(2k+1)(2k+2)
=2k·1·3·5·…·(2k-1)(2k+1)·2=2k+1·1·3·5·…·(2k-1)(2k+1),这就是说当n=k+1时等式也成立.
综上可知原等式对于任意正整数n都成立.[巧练模拟]——————(课堂突破保分题,分分必保!)[冲关锦囊]
用数学归纳法证明恒等式应注意
(1)明确初始值n0的取值并验证n=n0时等式成立.
(2)由n=k证明n=k+1时,弄清左边增加的项,且明确变
形目标.
(3)掌握恒等变形常用的方法:①因式分解;②添拆项;
③配方法.若x1,x2,…,xn为正数,则(1-x1)·(1-x2)·…·(1-xn)>1-(x1+x2+…+xn)(n≥2,n∈N).(*)
①当n=2时,∵x1>0,x2>0,∴(1-x1)(1-x2)=1-(x1+x2)+x1x2>1-(x1+x2).
②假设当n=k(k≥2)时,不等式成立,即若x1,x2,…,xk为正数,
则(1-x1)(1-x2)…(1-xk)>1-(x1+x2+…+xk),[冲关锦囊]
1.用数学归纳法证明与正整数n有关的不等式,一般有
三种具体形式:一是直接给出不等式,按要求进行证明;二是比较两个式子的大小,先利用n的几个特殊值猜想大小再给出证明;三是已知不等式成立,寻求变量的取值范围.
2.在证明由n=k到n=k+1成立时,一定要用归纳假设
n=k时得到的中间过渡式,由过渡式到目标式的证明可以用放缩法、基本不等式、分析法等.[例3] 数列{an}满足Sn=2n-an(n∈N*).
(1)计算a1,a2,a3,a4,并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.[巧练模拟][冲关锦囊] 解“归纳—猜想—证明”题的关键环节
(1)准确计算出前若干具体项,这是归纳、猜想的基础.
(2)通过观察、分析、比较、联想,猜想出一般结论.
(3)用数学归纳法证明之.[高手点拨]
1.解答本题时易忽略的步骤
(1)构造φ(x)后易忽略φ(x)的单调性的判断.尤其是其定义
域为(0,+∞)易忽视.
(2)在推证n=k+1时没有用上归纳假设.2.解答本题时易出现的错误
(1)不会由f(an+1)=g(an)联想到h(x)的零点问题,造成
归纳猜想时不分类讨论.
(2)分类讨论后,对于M的探索不会表述为M=max{x0,
a},从而得不出正确的证明.完全归纳法: 把研究对象一一都考查到了而推出结论的归纳法称为完全归纳法.
完全归纳法是一种在研究了事物的所有(有限种)特殊情况后得出一般结论的推理方法,又叫做枚举法.与不完全归纳法不同,用完全归纳法得出的结论是可靠的.通常在事物包括的特殊情况数不多时,采用完全归纳法 不完全归纳法 解释:从一类对象中部分对象都具有某种性质推出这类对象全体都具有这种性质的归纳推理方法。又作不完全归纳推理。
不完全归纳法是从一个或几个(但不是全部)特殊情况作出一般性结论的归纳推理.费尔马(费马猜想)结论是错误的。
对于某类事物,由它的一些特殊事例或其全部可能情况,
归纳出一般结论的推理方法,叫归纳法。?用不完全归纳法得出的结论不一定正确,如费马猜想。
?用完全归纳法得出的结论可靠,可不便操作。提出问题:如何找到一个科学有效的方法证明结论的
正确性呢?如何保证骨牌一一倒下? 需要几个步骤才能到?(1)处理第一个问题;(相当于推倒第一块骨牌)
(2)验证前一问题与后一问题有递推关系;
(相当于前牌推倒后牌)多米诺骨牌课件演示
数学归纳法的定义设{pn}是一个与自然数相关的命题集合,如果(1)证明起始命题p1(或p0)成立;
(2)在假设pk成立的前提下,推出pk+1也成立,那么可以断定。{pn}对一切正整数(或自然数)成立,这种方法叫做数学归纳法。 已知数列{an}中,a1=1,an+1=an/(an+1),用数学归纳法证明:
对所有的 正整数n,有an=1/na1=1成立假设ak=1/k成立,若证出
ak+1=1/(k+1)成立命题an=1/n成立命题成立类比 数学归纳法
证明一个与正整数n有关的命题,可按下列步骤:
1.(归纳奠基)证明当n取 时命题成立;2.(归纳递推)假设n=k(k≥n0,k∈N*)时命题成立,证明当
时命题也成立.
只要完成这两个步骤,就可以断定命题对从n0开始的所
有正整数n都成立.第一个值n0(n0∈N*)n=k+1答案: B 解析 :∵n为偶数故假设n=k成立后,再证n=k+2时等式成立.答案: D2.用数学归纳法证明“1+2+22+…+2n+2=2n+3-
1”,在验证n=1时,左边计算所得的式子为 ( )
A.1 B.1+2
C.1+2+22 D.1+2+22+23解析:由n=1时,左=1+2+22+23.答案: D答案:2k答案: 3解析:第一步检验的第一个值n0应为3. 数学归纳法的应用
(1)数学归纳法是一种只适用于与正整数有关的命题的证
明方法,它们的表述严格而且规范,两个步骤缺一不可.第一步是递推的基础,第二步是递推的依据,第二步中,归纳假设起着“已知条件”的作用,在n=k+1时一定要运用它,否则就不是数学归纳法.第二步的关键是“一凑假设,二凑结论”.
(2)在用数学归纳法证明问题的过程中,要注意从k到k+1
时命题中的项与项数的变化,防止对项数估算错误.[例1] 求证:(n+1)(n+2)·…·(n+n)=2n·1·3·5·…·(2n-1)(n∈N*).[自主解答] 当n=1时,等式左边=2,右边=2,故等式成立;假设当n=k时等式成立,
即(k+1)(k+2)·…·(k+k)=2k·1·3·5·…·(2k-1),
那么当n=k+1时,
左边=(k+1+1)(k+1+2)·…·(k+1+k+1)
=(k+2)(k+3)·…·(k+k)(2k+1)(2k+2)
=2k·1·3·5·…·(2k-1)(2k+1)·2=2k+1·1·3·5·…·(2k-1)(2k+1),这就是说当n=k+1时等式也成立.
综上可知原等式对于任意正整数n都成立.[巧练模拟]——————(课堂突破保分题,分分必保!)[冲关锦囊]
用数学归纳法证明恒等式应注意
(1)明确初始值n0的取值并验证n=n0时等式成立.
(2)由n=k证明n=k+1时,弄清左边增加的项,且明确变
形目标.
(3)掌握恒等变形常用的方法:①因式分解;②添拆项;
③配方法.若x1,x2,…,xn为正数,则(1-x1)·(1-x2)·…·(1-xn)>1-(x1+x2+…+xn)(n≥2,n∈N).(*)
①当n=2时,∵x1>0,x2>0,∴(1-x1)(1-x2)=1-(x1+x2)+x1x2>1-(x1+x2).
②假设当n=k(k≥2)时,不等式成立,即若x1,x2,…,xk为正数,
则(1-x1)(1-x2)…(1-xk)>1-(x1+x2+…+xk),[冲关锦囊]
1.用数学归纳法证明与正整数n有关的不等式,一般有
三种具体形式:一是直接给出不等式,按要求进行证明;二是比较两个式子的大小,先利用n的几个特殊值猜想大小再给出证明;三是已知不等式成立,寻求变量的取值范围.
2.在证明由n=k到n=k+1成立时,一定要用归纳假设
n=k时得到的中间过渡式,由过渡式到目标式的证明可以用放缩法、基本不等式、分析法等.[例3] 数列{an}满足Sn=2n-an(n∈N*).
(1)计算a1,a2,a3,a4,并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.[巧练模拟][冲关锦囊] 解“归纳—猜想—证明”题的关键环节
(1)准确计算出前若干具体项,这是归纳、猜想的基础.
(2)通过观察、分析、比较、联想,猜想出一般结论.
(3)用数学归纳法证明之.[高手点拨]
1.解答本题时易忽略的步骤
(1)构造φ(x)后易忽略φ(x)的单调性的判断.尤其是其定义
域为(0,+∞)易忽视.
(2)在推证n=k+1时没有用上归纳假设.2.解答本题时易出现的错误
(1)不会由f(an+1)=g(an)联想到h(x)的零点问题,造成
归纳猜想时不分类讨论.
(2)分类讨论后,对于M的探索不会表述为M=max{x0,
a},从而得不出正确的证明.完全归纳法: 把研究对象一一都考查到了而推出结论的归纳法称为完全归纳法.
完全归纳法是一种在研究了事物的所有(有限种)特殊情况后得出一般结论的推理方法,又叫做枚举法.与不完全归纳法不同,用完全归纳法得出的结论是可靠的.通常在事物包括的特殊情况数不多时,采用完全归纳法 不完全归纳法 解释:从一类对象中部分对象都具有某种性质推出这类对象全体都具有这种性质的归纳推理方法。又作不完全归纳推理。
不完全归纳法是从一个或几个(但不是全部)特殊情况作出一般性结论的归纳推理.费尔马(费马猜想)结论是错误的。
