3.1.3 复数的几何意义 课件(20张PPT)
文档属性
| 名称 | 3.1.3 复数的几何意义 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 685.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:34:50 | ||
图片预览





文档简介
(共20张PPT)
3.1.3复数的几何意义
教材:人教B版选修2-2
授课年级:高二年级
在几何上,我们用什么来表示实数?
实数的几何意义
类比实数的表示,可以用什么来表示复数?
实数可以用数轴上的点来表示。
实数
数轴上的点
(形)
(数)
一一对应
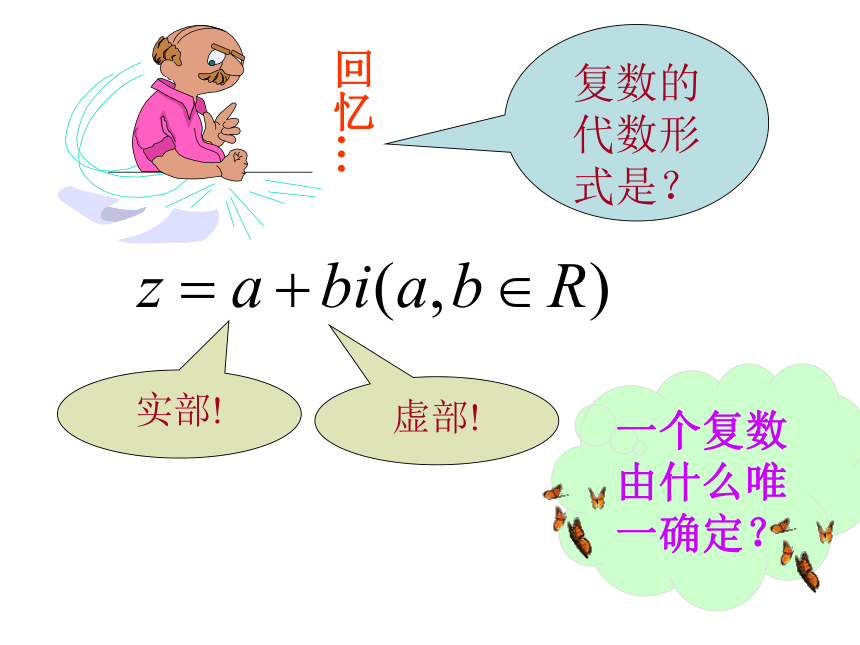
复数的代数形式是?
实部!
虚部!
一个复数由什么唯一确定?
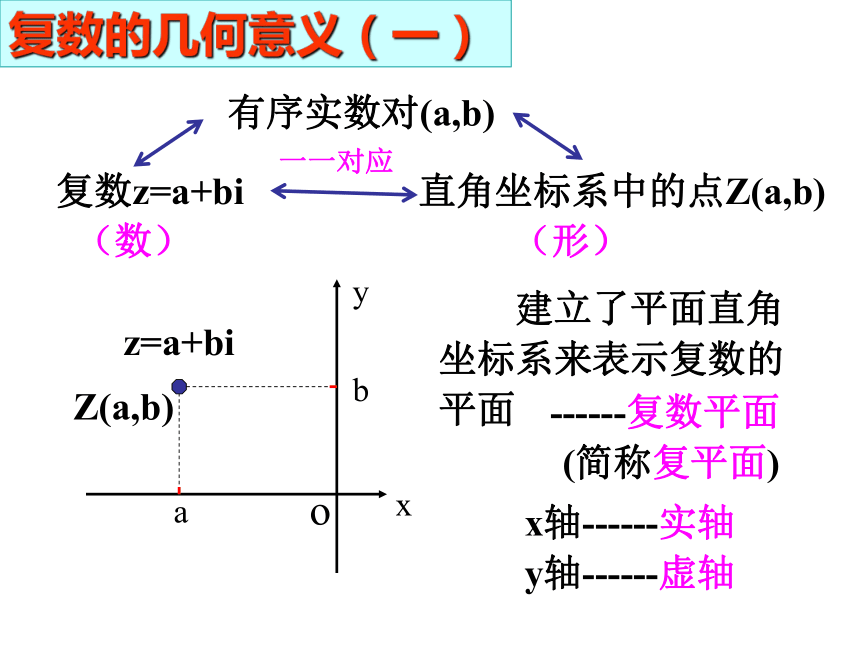
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x
y
o
b
a
Z(a,b)
建立了平面直角坐标系来表示复数的平面
x轴------实轴
y轴------虚轴
(数)
(形)
------复数平面 (简称复平面)
一一对应
z=a+bi
复数的几何意义(一)
例1 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-6)-2(m2+m-2)+4=0,
∴m=1或m=-2。
变式二:证明对一切实数m,复数z=(m2+m-6)+(m2+m-2)i所对应的点不可能位于第四象限。
不等式解集为空集
所以复数所对应的点不可能位于第四象限.
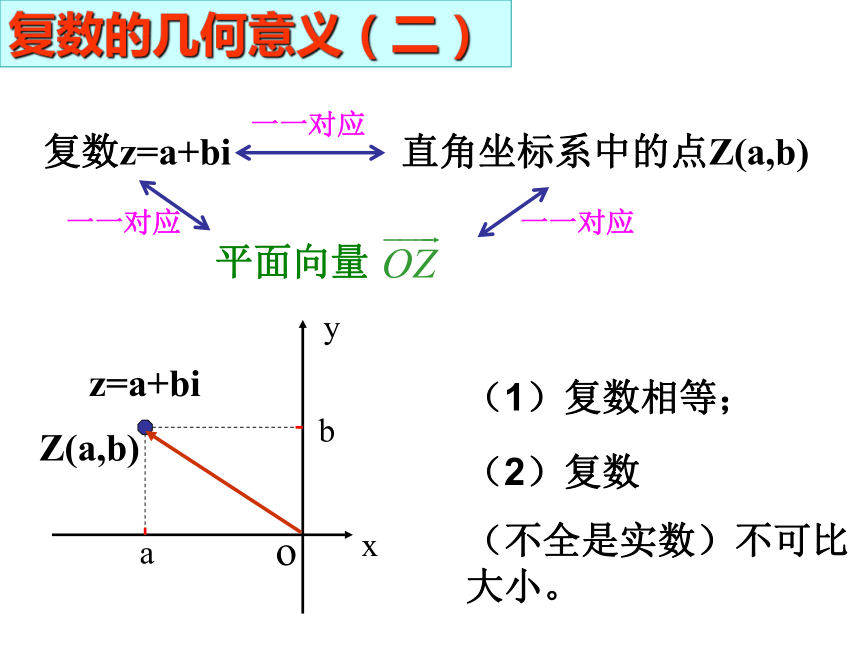
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
一一对应
一一对应
复数的几何意义(二)
x
y
o
b
a
Z(a,b)
z=a+bi
(1)复数相等;
(2)复数
(不全是实数)不可比大小。
它的模等于
(1)定义:
向量
的模r叫做复数
的模
记作
或
如果b=0,那么
是一个实数a,
(就是a的绝对值)
(2)模长公式:由模的定义可知:
(3)模的几何意义:
复数的模
x
O
z=a+bi
y
复数的绝对值
(复数的模)
的几何意义:
Z (a,b)
对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。
(2)满足|z|=4(z∈C)的z值有几个?
思考:
(1)满足|z|=4(z∈R)的z值有几个?
这些复数对应的点在复平面上构成怎样的图形?
x
y
O
设z=x+yi(x,y∈R)
满足|z|=4(z∈C)的复数z对应的点在复平面上将构成怎样的图形?
4
4
–4
–4
思考:
复数对应的点在复平面上构成怎样的图形?
如果两个复数的实部相等,而虚部互为相反数.
(1) 两个共轭复数对应的点有什么关系?
(2) 两个共轭复数对应的模有什么关系?
解:
1.知识层面
2.能力层面
3.情感态度价值观层面
成才之路:229-230页
A B组(必做)、C组(选做)
3.1.3复数的几何意义
教材:人教B版选修2-2
授课年级:高二年级
在几何上,我们用什么来表示实数?
实数的几何意义
类比实数的表示,可以用什么来表示复数?
实数可以用数轴上的点来表示。
实数
数轴上的点
(形)
(数)
一一对应
复数的代数形式是?
实部!
虚部!
一个复数由什么唯一确定?
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x
y
o
b
a
Z(a,b)
建立了平面直角坐标系来表示复数的平面
x轴------实轴
y轴------虚轴
(数)
(形)
------复数平面 (简称复平面)
一一对应
z=a+bi
复数的几何意义(一)
例1 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-6)-2(m2+m-2)+4=0,
∴m=1或m=-2。
变式二:证明对一切实数m,复数z=(m2+m-6)+(m2+m-2)i所对应的点不可能位于第四象限。
不等式解集为空集
所以复数所对应的点不可能位于第四象限.
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
一一对应
一一对应
复数的几何意义(二)
x
y
o
b
a
Z(a,b)
z=a+bi
(1)复数相等;
(2)复数
(不全是实数)不可比大小。
它的模等于
(1)定义:
向量
的模r叫做复数
的模
记作
或
如果b=0,那么
是一个实数a,
(就是a的绝对值)
(2)模长公式:由模的定义可知:
(3)模的几何意义:
复数的模
x
O
z=a+bi
y
复数的绝对值
(复数的模)
的几何意义:
Z (a,b)
对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。
(2)满足|z|=4(z∈C)的z值有几个?
思考:
(1)满足|z|=4(z∈R)的z值有几个?
这些复数对应的点在复平面上构成怎样的图形?
x
y
O
设z=x+yi(x,y∈R)
满足|z|=4(z∈C)的复数z对应的点在复平面上将构成怎样的图形?
4
4
–4
–4
思考:
复数对应的点在复平面上构成怎样的图形?
如果两个复数的实部相等,而虚部互为相反数.
(1) 两个共轭复数对应的点有什么关系?
(2) 两个共轭复数对应的模有什么关系?
解:
1.知识层面
2.能力层面
3.情感态度价值观层面
成才之路:229-230页
A B组(必做)、C组(选做)
