人教B版 选修2-2 第三章复数复习(31张PPT)
文档属性
| 名称 | 人教B版 选修2-2 第三章复数复习(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 838.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
复数复习课
课程标准要求
1、理解复数的基本概念;
2、理解复数相等的充要条件;
3、能进行复数代数形式的四则运算;
4、了解复数的代数表示法及其几何意义;
5、了解复数代数形式的加、减运算的几 何意义
.
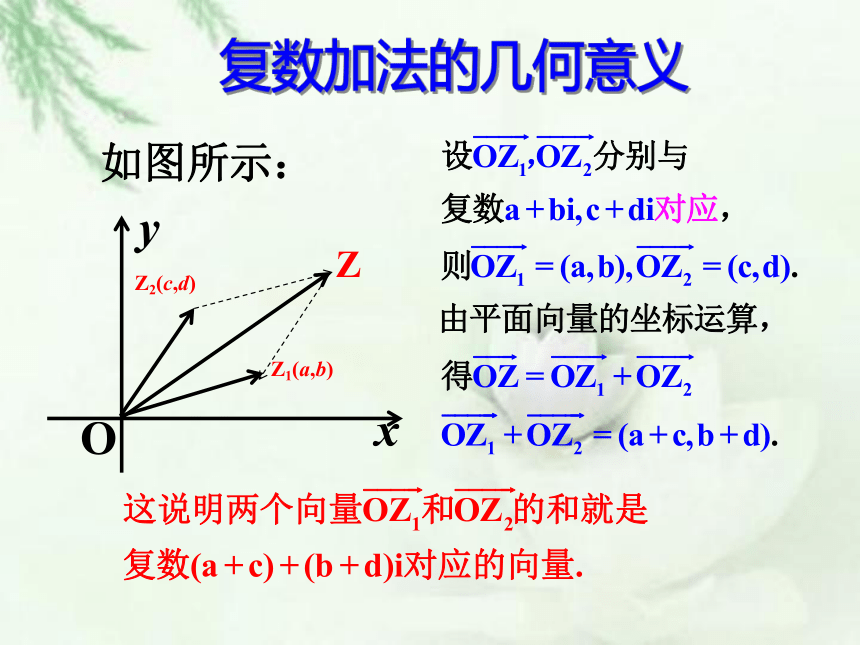
如图所示:
课程标准要求
1、理解复数的基本概念;
2、理解复数相等的充要条件;
3、能进行复数代数形式的四则运算;
4、了解复数的代数表示法及其几何意义;
5、了解复数代数形式的加、减运算的几 何意义
.
D
选择
我们规定,复数的加法法则如下:
很明显,两个复数的和仍然是一个确定的复数.
设z1=a+bi, z2=c+di 是任意两个复数,那么
(a+bi)+(c+di)=(a+c)+(b+d)i.
即:两个复数相加就是
实部与实部,虚部与虚部分别相加.
复数的加法满足交换律、结合律
(a+bi)-(c+di)=(a-c)+(b-d)i.
复数的减法就是加法的逆运算.
复数的减法法则:
实部与实部,虚部与虚部分别相减.
由此可见,两个复数的差是一个确定的复数.
我们规定,复数的乘法法则如下:
设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积
复数的乘法与多项式的乘法是类似的,只要把结果中i2换成-1,把实部与虚部分别合并即可。
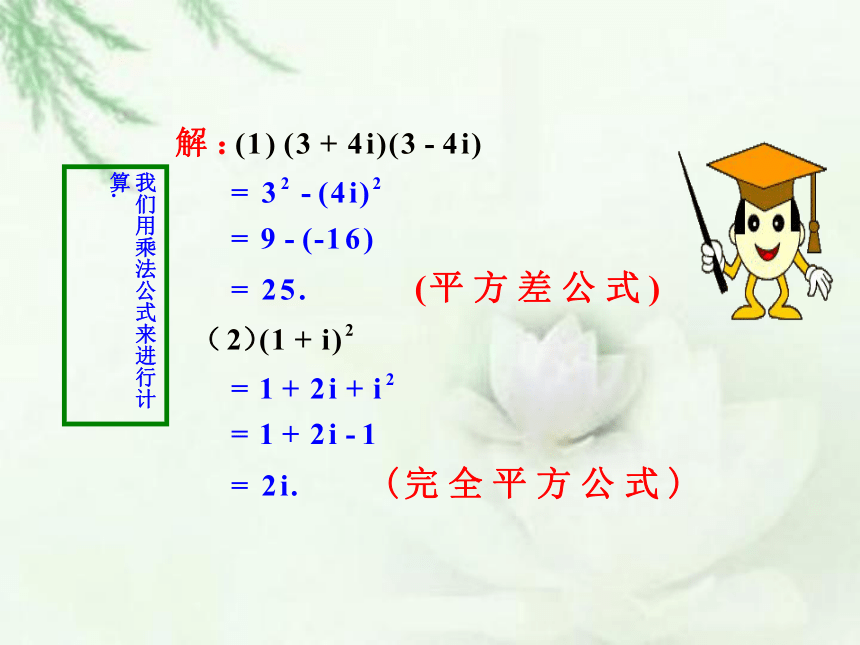
我们用乘法公式来进行计算.
若Z1,Z2,是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
( )
(2)Z1Z2是一个怎样的数?( )
复数z=a+bi的共轭复数记作
动动脑
关于X轴对称
实数
除法法则:
先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后再化简.
课程标准要求
1、理解复数的基本概念;
2、理解复数相等的充要条件;
3、了解复数的代数表示法及其几何意义;
4、会进行复数代数形式的四则运算。
.
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】
?
?
?
【解题过程】
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】复数相等的概念,考查考生对复数的运算求解能力。
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】复数相等的概念,考查考生对复数的运算求解能力。
【解题过程】由题设可得
根据复数相等的概念,
可知x=1,x=y,故y=1
1、复数的定义:设a,b都是实数,形如
的数叫做复数,即
a叫做复数z的实部,b叫做复数z的虚部。
2、 为实数 b=0
为虚数
3、
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】
【解题过程】
【考查目标】复数的代数表示形式、复数的几何意义以及复平面四个象限内点的坐标的特征。
【解题过程】
【考查目标】复数的代数表示形式、复数的几何意义以及复平面四个象限内点的坐标的特征。
【解题过程】复数在复平面内对应的点位于第四象限,所以
得实数m的解集为(-3,1),选择A。
1、复数的几何意义
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
一一对应
一一对应
x
y
o
b
a
Z(a,b)
z=a+bi
2、复数的绝对值(复数的模)的几何意义:
x
O
z=a+bi
y
Z (a,b)
【考查目标】
【解题思路】
【考查目标】复数的代数表示形式、共轭复数及其性质以及复数的简单运算。
【解题思路】
【考查目标】复数的代数表示形式、共轭复数及其性质以及复数的简单运算。
【解题思路】由 得
知
所以 故选C
所以
显然,复数的倒数还是复数,并且具有唯一性;
有了倒数,我们就可以做复数的除法运算:
例2 计算
高考链接
2014年高考(全国卷I理2)
( )
A B C D
2014年高考(全国卷I文2)
设 ,则 ( )
A B C D
高考链接
2016年高考(天津卷理9)
是虚数单位,复数 满足 , 的实部是( )
2015年高考(安徽卷理1)
设 是虚数单位,则复数 在复平面内所对应的点位于( )
A. 第一象限 B, 第二象限 C. 第三象限 D. 第四象限
小结
今天的学习收获有哪些?
1、会求复数的倒数。
2、学习了复数的除法运算法则,其实质是复数商的分母实数化,即分子分母同乘分母的共轭复数。
3、复数的除法运算的一般步骤
复数复习课
课程标准要求
1、理解复数的基本概念;
2、理解复数相等的充要条件;
3、能进行复数代数形式的四则运算;
4、了解复数的代数表示法及其几何意义;
5、了解复数代数形式的加、减运算的几 何意义
.
如图所示:
课程标准要求
1、理解复数的基本概念;
2、理解复数相等的充要条件;
3、能进行复数代数形式的四则运算;
4、了解复数的代数表示法及其几何意义;
5、了解复数代数形式的加、减运算的几 何意义
.
D
选择
我们规定,复数的加法法则如下:
很明显,两个复数的和仍然是一个确定的复数.
设z1=a+bi, z2=c+di 是任意两个复数,那么
(a+bi)+(c+di)=(a+c)+(b+d)i.
即:两个复数相加就是
实部与实部,虚部与虚部分别相加.
复数的加法满足交换律、结合律
(a+bi)-(c+di)=(a-c)+(b-d)i.
复数的减法就是加法的逆运算.
复数的减法法则:
实部与实部,虚部与虚部分别相减.
由此可见,两个复数的差是一个确定的复数.
我们规定,复数的乘法法则如下:
设z1=a+bi, z2=c+di 是任意两个复数,那么它们的积
复数的乘法与多项式的乘法是类似的,只要把结果中i2换成-1,把实部与虚部分别合并即可。
我们用乘法公式来进行计算.
若Z1,Z2,是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
( )
(2)Z1Z2是一个怎样的数?( )
复数z=a+bi的共轭复数记作
动动脑
关于X轴对称
实数
除法法则:
先把两个复数相除写成分数形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后再化简.
课程标准要求
1、理解复数的基本概念;
2、理解复数相等的充要条件;
3、了解复数的代数表示法及其几何意义;
4、会进行复数代数形式的四则运算。
.
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】
?
?
?
【解题过程】
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】复数相等的概念,考查考生对复数的运算求解能力。
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】复数相等的概念,考查考生对复数的运算求解能力。
【解题过程】由题设可得
根据复数相等的概念,
可知x=1,x=y,故y=1
1、复数的定义:设a,b都是实数,形如
的数叫做复数,即
a叫做复数z的实部,b叫做复数z的虚部。
2、 为实数 b=0
为虚数
3、
例1、(16全国一 改编)设
,其中x,y是实数,则
【考查目标】
【解题过程】
【考查目标】复数的代数表示形式、复数的几何意义以及复平面四个象限内点的坐标的特征。
【解题过程】
【考查目标】复数的代数表示形式、复数的几何意义以及复平面四个象限内点的坐标的特征。
【解题过程】复数在复平面内对应的点位于第四象限,所以
得实数m的解集为(-3,1),选择A。
1、复数的几何意义
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
一一对应
一一对应
x
y
o
b
a
Z(a,b)
z=a+bi
2、复数的绝对值(复数的模)的几何意义:
x
O
z=a+bi
y
Z (a,b)
【考查目标】
【解题思路】
【考查目标】复数的代数表示形式、共轭复数及其性质以及复数的简单运算。
【解题思路】
【考查目标】复数的代数表示形式、共轭复数及其性质以及复数的简单运算。
【解题思路】由 得
知
所以 故选C
所以
显然,复数的倒数还是复数,并且具有唯一性;
有了倒数,我们就可以做复数的除法运算:
例2 计算
高考链接
2014年高考(全国卷I理2)
( )
A B C D
2014年高考(全国卷I文2)
设 ,则 ( )
A B C D
高考链接
2016年高考(天津卷理9)
是虚数单位,复数 满足 , 的实部是( )
2015年高考(安徽卷理1)
设 是虚数单位,则复数 在复平面内所对应的点位于( )
A. 第一象限 B, 第二象限 C. 第三象限 D. 第四象限
小结
今天的学习收获有哪些?
1、会求复数的倒数。
2、学习了复数的除法运算法则,其实质是复数商的分母实数化,即分子分母同乘分母的共轭复数。
3、复数的除法运算的一般步骤
