数系的扩充和复数的概念
图片预览







文档简介
(共35张PPT)
计数的需要
正整数
零
自然数
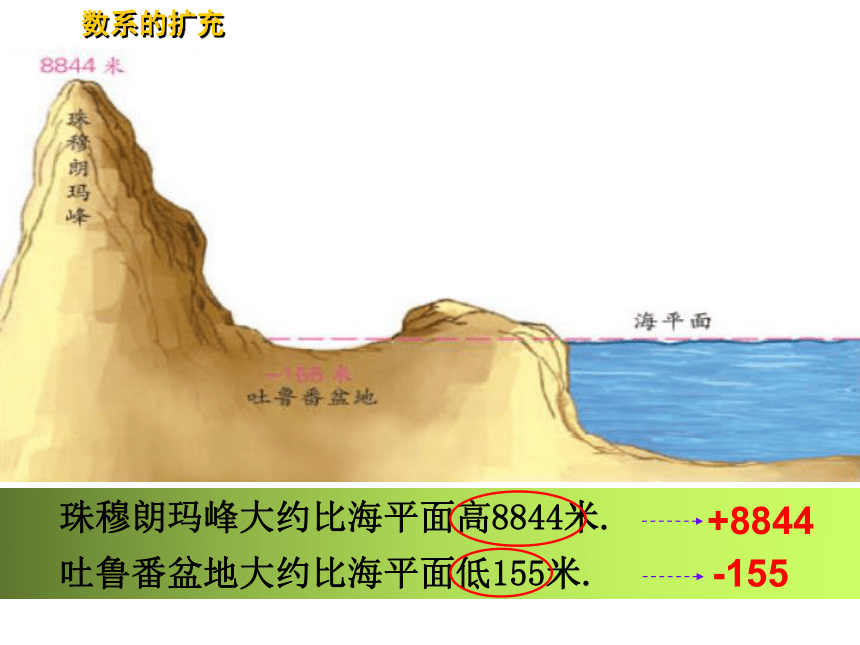
珠穆朗玛峰大约比海平面高8844米.
吐鲁番盆地大约比海平面低155米.
+8844
-155
中国是世界上最早认识应用负数的
国家.早在2000多年前的《九章算术》
中,就有正数和负数的记载.在古代人民
生活中,以收入钱为正,以支出钱为负.在
粮食生产中,以产量增加为正,以产量减
少为负.古代的人们为区别正、负数,常
用红色算筹表示正,黑色算筹表示负.
小贴士
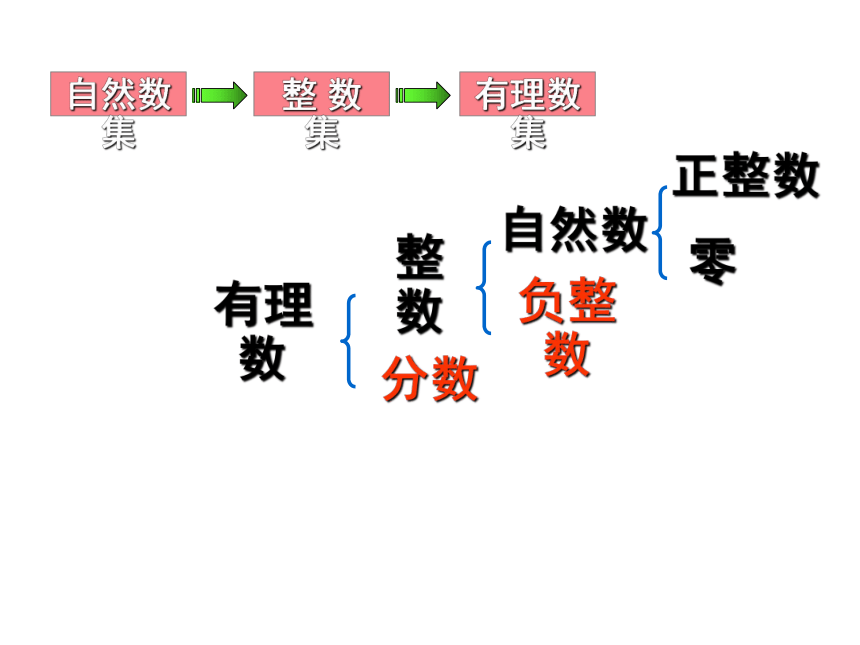
自然数集
整数
负整数
自然数
正整数
零
整 数 集
整数
负整数
自然数
正整数
零
分数
有理数
有理数集
毕达哥拉斯(约公元前560—480年)
“数”是万物的本源,支配整个自然界和人类社会.世间一切事物都可归结为数或数的比例,这是世界所以美好和谐的源泉.
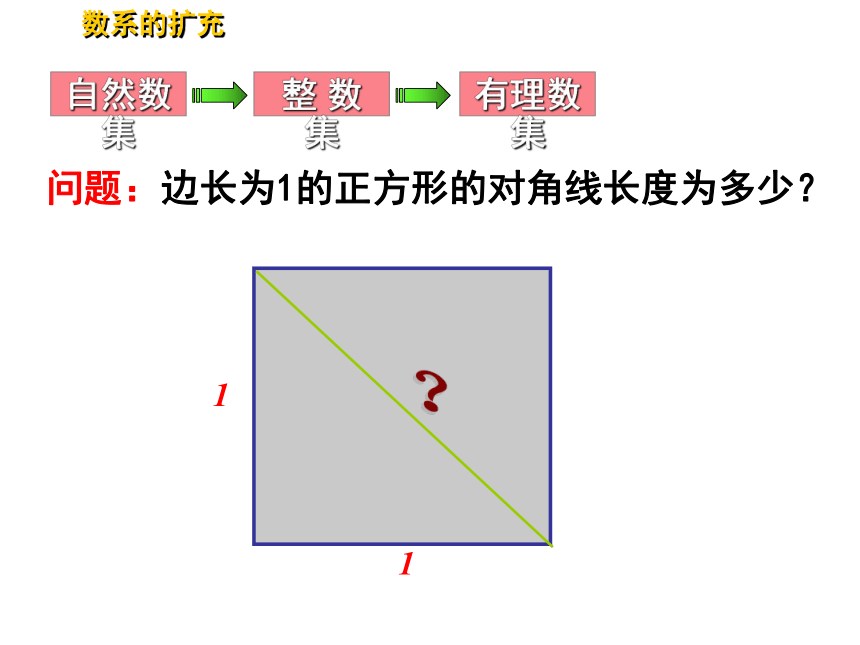
1
1
问题:边长为1的正方形的对角线长度为多少?
无理数
实数
实 数 集
提出问题
解:设其中一个数是 x ,则另一个数为10-x.
化简得: x2-10x+40=0
五百年前意大利的卡尔丹遇到这样一个问题
将10分成两个部分,使它们的乘积等于40.
该方程无实数解
则 x (10-x) =40
学生活动
我们,如何来解决这个问题?
讨论
1545年,卡尔丹在《大衍术》中写道:“要把10分成两部分,使二者乘积为40,这是不可能的,不过我却用下列方式解决了.”
能作为“数”吗?
它表示什么意义?
历史回顾
1637年,法国数学家笛卡尔把这样的数叫做“虚数”
(R.Descartes,1596--1661)
笛卡尔
imaginary
一.新数 i 叫做虚数单位,并规定:
(1)i 2 ? ?1;
(2)实数可以与 i 进行四则运算,在进
行四则运算时,原有的加法与乘法
的运算律仍然成立.
(1)形如a+bi(a,b∈R)的数叫做复数,
通常用字母 z 表示.
(3)全体复数所形成的集合叫做复数
集,一般用字母 C 表示.
二.复数的概念
实部
虚部
其中i称为虚数单位.
(2)
例1.写出下列复数的实部与虚部.
解: 4的实部为 4 ,虚部为 0 ;
2-3i的实部为 2 ,虚部为 -3 ;
0的实部为 0 ,虚部为 0 ;
6i的实部为 0 ,虚部为 6 。
三、复数的分类
复数a+bi
如图所示:
虚数集
实数集
纯虚数集
例2 实数m取什么值时,
复数 是
(1)实数(2)虚数(3)纯虚数
(4)0
(5)6+2i
例2 实数m取什么值时,
复数 是
(1)实数(2)虚数(3)纯虚数
如何定义两个复数相等?
反之,也成立.
四. 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
复数的概念
想一想
复数相等的问题
转化
求方程组的解的问题
转化(复数问题实数化)
解: 根据两个复数相等的充要条件, 可得方程组
求实数x和y
1.数系的扩充;
回顾反思
1.请说出下列复数的实部和虚部,并判断它们是实数,虚数还是纯虚数。
0
2、课本106页--第2题
学完本节课,卡尔丹的问题能解决了吗?
解决问题
作业:课本P106/习题3.1A组第3题
课后思考:
数系还能再扩充吗?
1
-1
B
拓展提升
?
与君共勉
数学是无穷的科学。
问题是数学的心脏。
路漫漫其修远兮,吾将上下而求索。
计数的需要
正整数
零
自然数
珠穆朗玛峰大约比海平面高8844米.
吐鲁番盆地大约比海平面低155米.
+8844
-155
中国是世界上最早认识应用负数的
国家.早在2000多年前的《九章算术》
中,就有正数和负数的记载.在古代人民
生活中,以收入钱为正,以支出钱为负.在
粮食生产中,以产量增加为正,以产量减
少为负.古代的人们为区别正、负数,常
用红色算筹表示正,黑色算筹表示负.
小贴士
自然数集
整数
负整数
自然数
正整数
零
整 数 集
整数
负整数
自然数
正整数
零
分数
有理数
有理数集
毕达哥拉斯(约公元前560—480年)
“数”是万物的本源,支配整个自然界和人类社会.世间一切事物都可归结为数或数的比例,这是世界所以美好和谐的源泉.
1
1
问题:边长为1的正方形的对角线长度为多少?
无理数
实数
实 数 集
提出问题
解:设其中一个数是 x ,则另一个数为10-x.
化简得: x2-10x+40=0
五百年前意大利的卡尔丹遇到这样一个问题
将10分成两个部分,使它们的乘积等于40.
该方程无实数解
则 x (10-x) =40
学生活动
我们,如何来解决这个问题?
讨论
1545年,卡尔丹在《大衍术》中写道:“要把10分成两部分,使二者乘积为40,这是不可能的,不过我却用下列方式解决了.”
能作为“数”吗?
它表示什么意义?
历史回顾
1637年,法国数学家笛卡尔把这样的数叫做“虚数”
(R.Descartes,1596--1661)
笛卡尔
imaginary
一.新数 i 叫做虚数单位,并规定:
(1)i 2 ? ?1;
(2)实数可以与 i 进行四则运算,在进
行四则运算时,原有的加法与乘法
的运算律仍然成立.
(1)形如a+bi(a,b∈R)的数叫做复数,
通常用字母 z 表示.
(3)全体复数所形成的集合叫做复数
集,一般用字母 C 表示.
二.复数的概念
实部
虚部
其中i称为虚数单位.
(2)
例1.写出下列复数的实部与虚部.
解: 4的实部为 4 ,虚部为 0 ;
2-3i的实部为 2 ,虚部为 -3 ;
0的实部为 0 ,虚部为 0 ;
6i的实部为 0 ,虚部为 6 。
三、复数的分类
复数a+bi
如图所示:
虚数集
实数集
纯虚数集
例2 实数m取什么值时,
复数 是
(1)实数(2)虚数(3)纯虚数
(4)0
(5)6+2i
例2 实数m取什么值时,
复数 是
(1)实数(2)虚数(3)纯虚数
如何定义两个复数相等?
反之,也成立.
四. 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
复数的概念
想一想
复数相等的问题
转化
求方程组的解的问题
转化(复数问题实数化)
解: 根据两个复数相等的充要条件, 可得方程组
求实数x和y
1.数系的扩充;
回顾反思
1.请说出下列复数的实部和虚部,并判断它们是实数,虚数还是纯虚数。
0
2、课本106页--第2题
学完本节课,卡尔丹的问题能解决了吗?
解决问题
作业:课本P106/习题3.1A组第3题
课后思考:
数系还能再扩充吗?
1
-1
B
拓展提升
?
与君共勉
数学是无穷的科学。
问题是数学的心脏。
路漫漫其修远兮,吾将上下而求索。
