3.1.2 复数的概念 课件(21张PPT)
文档属性
| 名称 | 3.1.2 复数的概念 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 474.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:37:16 | ||
图片预览







文档简介
课件21张PPT。3.1.1《数系的扩充
与复数的概念》人教B版选修2——2第三章教学目标理解数系的扩充是与生活密切相关的,明白复数及其相关概念。
教学重点:复数及其相关概念,能区分虚数与纯虚数,明白各数系的关系。
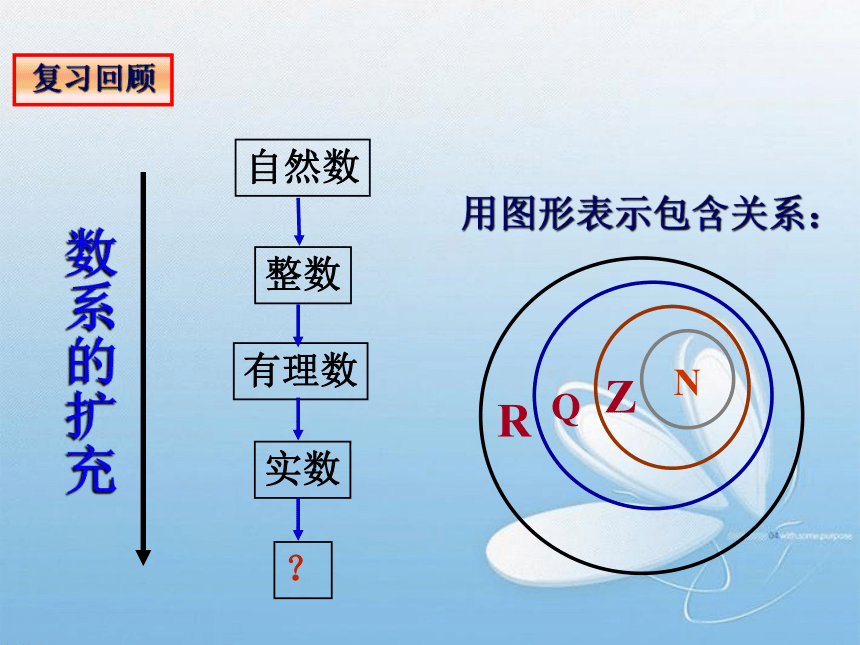
教学难点:复数及其相关概念的理解 引言:在人和社会的发展过程中,常常需要立足今天,回顾昨天,展望明天。符合客观发展规律的要发扬和完善,不符合的要否定和抛弃。那么,在实数集向复数集发展的过程中,我们应该如何发扬和完善,否定和抛弃呢?数系的扩充用图形表示包含关系:复习回顾知识引入引入一个新数: 现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集,
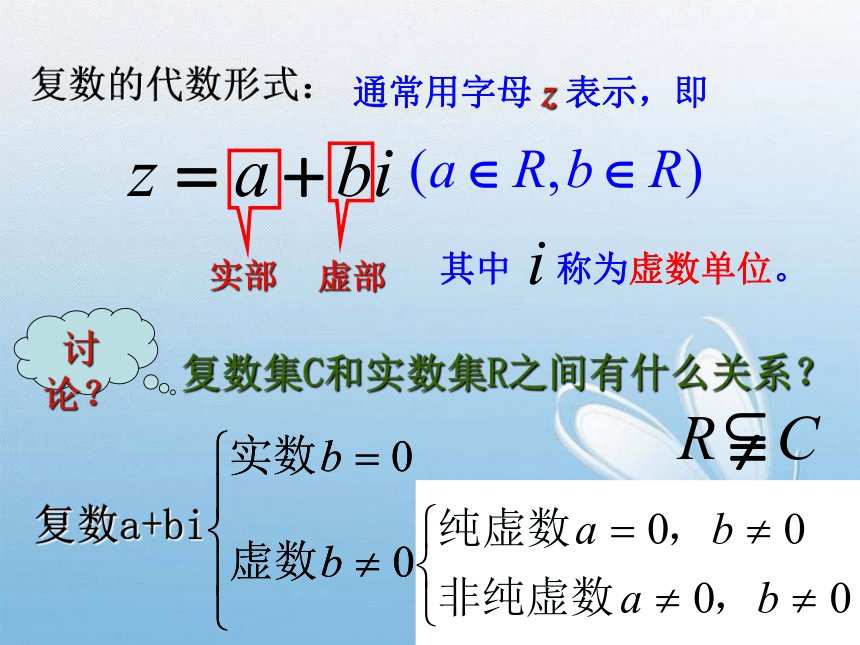
一般用字母C表示 .复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。复数a+bi复数集,虚数集,实数集,纯虚数集之间的关系? 思 考?复数集虚数集实数集纯虚数集练一练:1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。 2.已知复数 当a为何值时,z分别为(1)实数(2)虚数 (3)纯虚数思考:如何定义两个复数的相等?注意:一般对两个复数只能说相等或不相等;不能比较大小。00 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.例1:已知 ,其中 求解题思考:复数相等的问题转化求方程组的解的问题一种重要的数学思想:转化思想3.x-y+(2x+y)i=x+y-2+(y+2)i,练一练:求x,y的值。4.求 的取值范围。小结:1.虚数单位i的引入;计算:1-1B复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi平面向量复数的几何意义:例2:复数z=-3-4i所表示的点在第几象限?练一练:5.若复数 所表示的点在第四象限,求x的取值范围。实数绝对值的几何意义:能否把绝对值概念推广到复数范围呢?XOAa| a | = | OA | 实数a在数轴上所对应的点A到原点O的距离。xOz=a+biy| z | = |OZ|复数的绝对值(复数的模)Z (a,b) 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。 例3 求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i(3)满足|z|=5(z∈C)的z值有几个?思考:(2)满足|z|=5(z∈R)的z值有几个?(1)复数的模能否比较大小? 这些复 数对应的点在复平面上构成怎样的图形? 图示xyO设z=x+yi(x,y∈R) 满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5共轭复数:Z= +bi的共轭复数为:(1)实部相等 虚部相反
(2)
(3)练一练:
6.z=m+(2m-4)i, 求m的值 。 小结(1)充分理解复数的基本概念;
(2)掌握基本知识要点,学会利用复数知识解决问题;
(3)提高基本计算能力,逻辑思维能力及知识综合能力。谢谢聆听
再见
与复数的概念》人教B版选修2——2第三章教学目标理解数系的扩充是与生活密切相关的,明白复数及其相关概念。
教学重点:复数及其相关概念,能区分虚数与纯虚数,明白各数系的关系。
教学难点:复数及其相关概念的理解 引言:在人和社会的发展过程中,常常需要立足今天,回顾昨天,展望明天。符合客观发展规律的要发扬和完善,不符合的要否定和抛弃。那么,在实数集向复数集发展的过程中,我们应该如何发扬和完善,否定和抛弃呢?数系的扩充用图形表示包含关系:复习回顾知识引入引入一个新数: 现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集,
一般用字母C表示 .复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。复数a+bi复数集,虚数集,实数集,纯虚数集之间的关系? 思 考?复数集虚数集实数集纯虚数集练一练:1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。 2.已知复数 当a为何值时,z分别为(1)实数(2)虚数 (3)纯虚数思考:如何定义两个复数的相等?注意:一般对两个复数只能说相等或不相等;不能比较大小。00 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.例1:已知 ,其中 求解题思考:复数相等的问题转化求方程组的解的问题一种重要的数学思想:转化思想3.x-y+(2x+y)i=x+y-2+(y+2)i,练一练:求x,y的值。4.求 的取值范围。小结:1.虚数单位i的引入;计算:1-1B复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi平面向量复数的几何意义:例2:复数z=-3-4i所表示的点在第几象限?练一练:5.若复数 所表示的点在第四象限,求x的取值范围。实数绝对值的几何意义:能否把绝对值概念推广到复数范围呢?XOAa| a | = | OA | 实数a在数轴上所对应的点A到原点O的距离。xOz=a+biy| z | = |OZ|复数的绝对值(复数的模)Z (a,b) 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。 例3 求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i(3)满足|z|=5(z∈C)的z值有几个?思考:(2)满足|z|=5(z∈R)的z值有几个?(1)复数的模能否比较大小? 这些复 数对应的点在复平面上构成怎样的图形? 图示xyO设z=x+yi(x,y∈R) 满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5共轭复数:Z= +bi的共轭复数为:(1)实部相等 虚部相反
(2)
(3)练一练:
6.z=m+(2m-4)i, 求m的值 。 小结(1)充分理解复数的基本概念;
(2)掌握基本知识要点,学会利用复数知识解决问题;
(3)提高基本计算能力,逻辑思维能力及知识综合能力。谢谢聆听
再见
