2.3.1 数学归纳法课件(17张PPT)
文档属性
| 名称 | 2.3.1 数学归纳法课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 937.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 08:57:24 | ||
图片预览




文档简介
(共17张PPT)
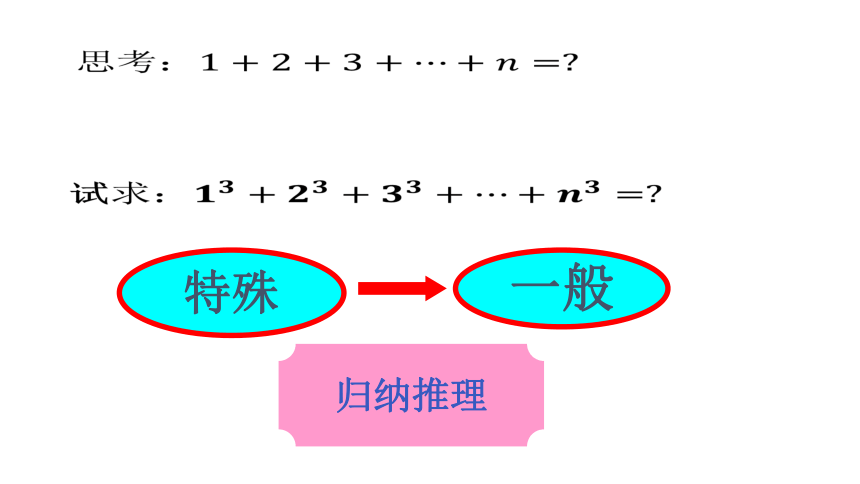
思考
试
归纳推理
特殊
一般
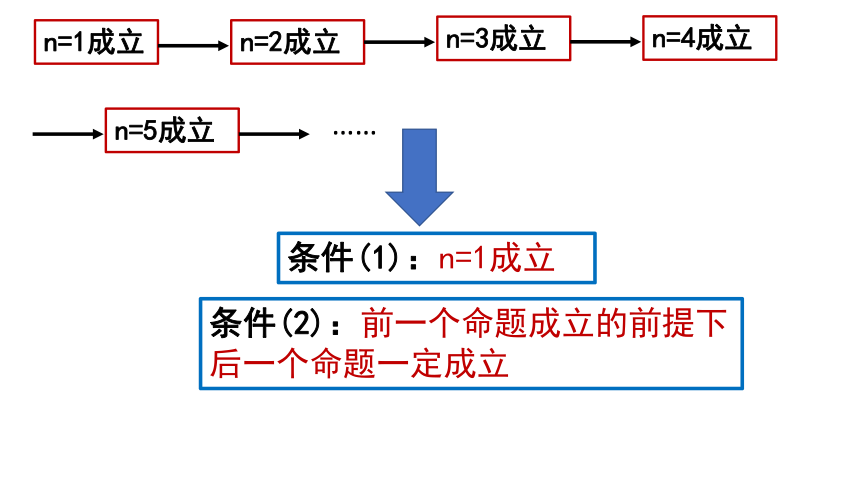
n=1成立
n=2成立
……
n=3成立
n=4成立
n=5成立
n=1成立
n=2成立
……
n=3成立
n=4成立
n=5成立
条件(1):n=1成立
条件(2):前一个命题成立的前提下
后一个命题一定成立
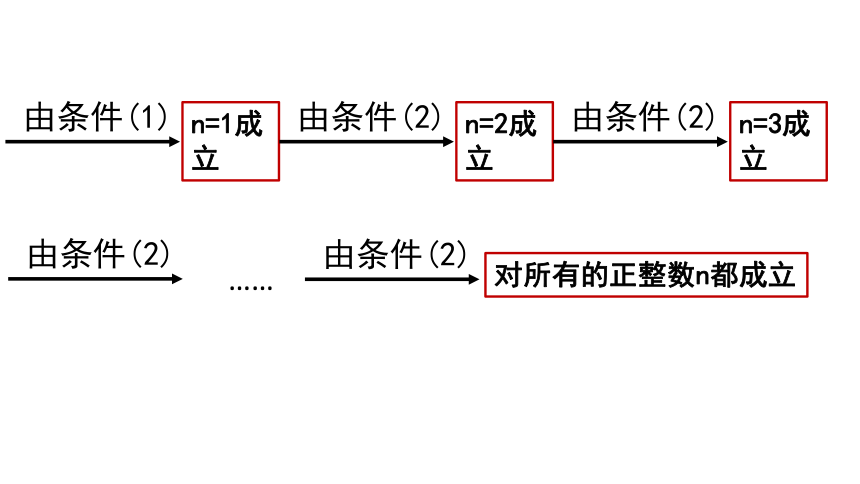
由条件(1)
n=1成立
由条件(2)
n=2成立
由条件(2)
n=3成立
由条件(2)
由条件(2)
对所有的正整数n都成立
……
?多米诺骨牌游戏
生活中的数学
思考:满足什么条件,骨牌可以全部倒下?
条件2:假如某一张牌倒下, 则它的后一张牌必定倒下。
骨牌可以全部倒下需要满足以下条件:
条件1:第一张骨牌被推倒;
由条件2
由条件1
第1块倒下
由条件2
第2块倒下
由条件2
第3块倒下
由条件2
第n块倒下
由条件2
所有骨牌全部倒下
……
骨牌
骨牌倒下
正整数n
命题P(n)成立
类比
无限
有限
?
任意相邻的两块牌,
前一块倒下一定导
致后一块牌倒下.
第一块
骨牌倒下
1
2
3
4
k
K+1
……
……
第一项成立
第k项成立,
第k+1项成立.
多米诺骨牌游戏的原理 与正整数有关的数学命题
(1)n=1时命题成立
,则n=k+1时结论也成立
根据(1)(2),可知对任意的正整数n,命题都成立
(1)第1块要倒下
(2)当前面一块倒下时,后面一块必须倒下
根据(1)(2),可知无论多少块骨牌都能全部倒下
数学归纳法
与正整数有关的数学命题
(1)n=1时命题成立
根据(1)(2),可知对任意的正整数n,命题都成立
猜想:
用数学归纳法证明
对 进行归纳猜想,
并用数学归纳法进行证明。
结论不一定可靠
考察部分对象,得到一般结论的推理方法
归纳法
不完全归纳法
结论一定可靠
考察全体对象,得到一般结论的推理方法
完全归纳法
(数学归纳法)
递推思想
思考
试
归纳推理
特殊
一般
n=1成立
n=2成立
……
n=3成立
n=4成立
n=5成立
n=1成立
n=2成立
……
n=3成立
n=4成立
n=5成立
条件(1):n=1成立
条件(2):前一个命题成立的前提下
后一个命题一定成立
由条件(1)
n=1成立
由条件(2)
n=2成立
由条件(2)
n=3成立
由条件(2)
由条件(2)
对所有的正整数n都成立
……
?多米诺骨牌游戏
生活中的数学
思考:满足什么条件,骨牌可以全部倒下?
条件2:假如某一张牌倒下, 则它的后一张牌必定倒下。
骨牌可以全部倒下需要满足以下条件:
条件1:第一张骨牌被推倒;
由条件2
由条件1
第1块倒下
由条件2
第2块倒下
由条件2
第3块倒下
由条件2
第n块倒下
由条件2
所有骨牌全部倒下
……
骨牌
骨牌倒下
正整数n
命题P(n)成立
类比
无限
有限
?
任意相邻的两块牌,
前一块倒下一定导
致后一块牌倒下.
第一块
骨牌倒下
1
2
3
4
k
K+1
……
……
第一项成立
第k项成立,
第k+1项成立.
多米诺骨牌游戏的原理 与正整数有关的数学命题
(1)n=1时命题成立
,则n=k+1时结论也成立
根据(1)(2),可知对任意的正整数n,命题都成立
(1)第1块要倒下
(2)当前面一块倒下时,后面一块必须倒下
根据(1)(2),可知无论多少块骨牌都能全部倒下
数学归纳法
与正整数有关的数学命题
(1)n=1时命题成立
根据(1)(2),可知对任意的正整数n,命题都成立
猜想:
用数学归纳法证明
对 进行归纳猜想,
并用数学归纳法进行证明。
结论不一定可靠
考察部分对象,得到一般结论的推理方法
归纳法
不完全归纳法
结论一定可靠
考察全体对象,得到一般结论的推理方法
完全归纳法
(数学归纳法)
递推思想
