“杨辉三角”与二项式系数的性质 课件(19张PPT)
文档属性
| 名称 | “杨辉三角”与二项式系数的性质 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览





文档简介
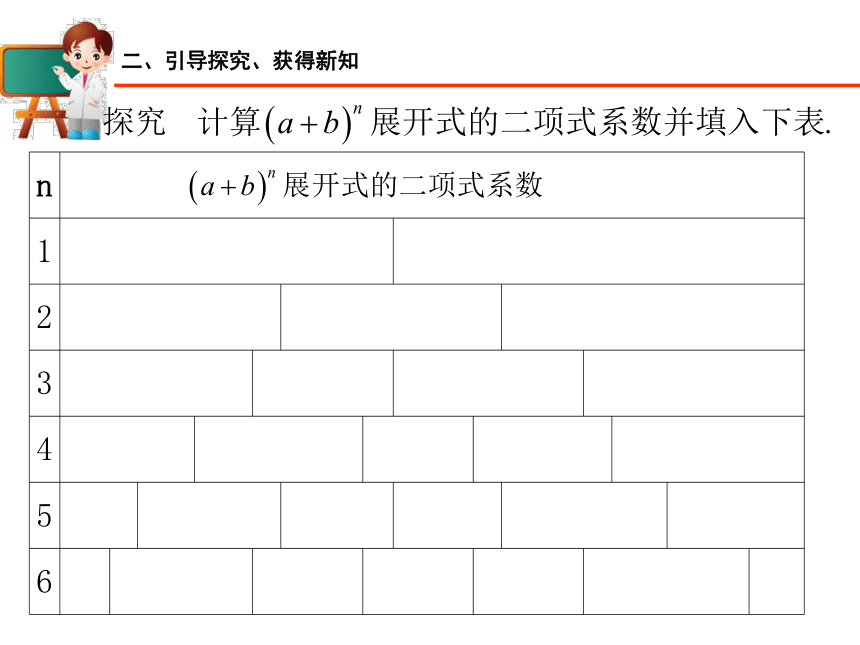
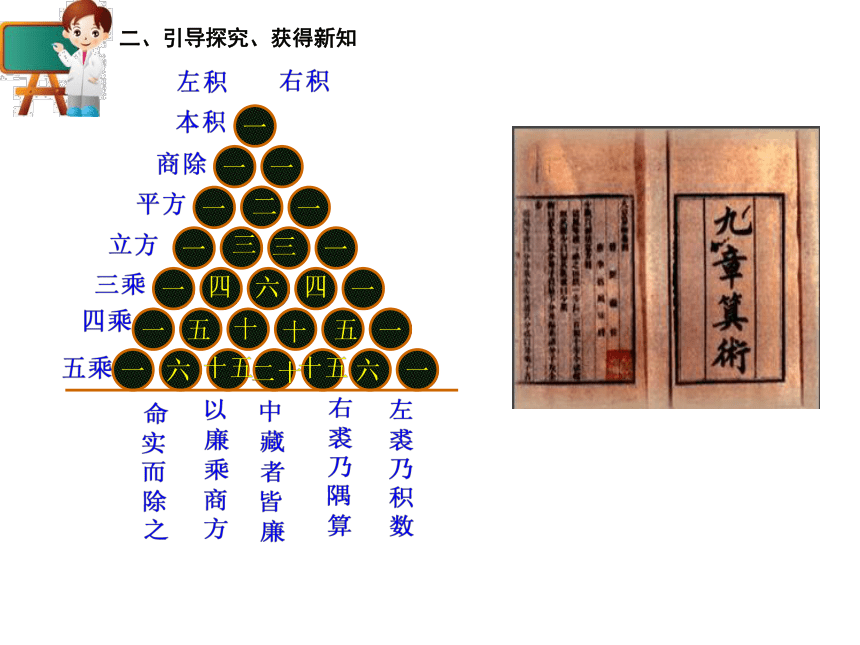
课件19张PPT。“杨辉三角”与二项式系数的性质教学基本流程复习旧知,自然引出所探究的问题学生动手写出二项式系数表,观察发现规律观察、讨论、归纳二项式系数的性质通过例题和练习,巩固对二项式系数的认识①二项式定理②二项展开式的通项③二项展开式中的二项式系数是哪些?(a+b)1(a+b)3(a+b)4(a+b)5(a+b)2(a+b)6二、引导探究、获得新知二、引导探究、获得新知贾宪杨辉布莱士?帕斯卡《释锁算书》
《黄帝九章算法细草》《详解九章算法》
《日用算法》
《杨辉算法》
《乘除变通本末》
《算术三角形》
《思想录》Chinese triangle问题1:观察杨辉三角的每一行数字,正数第1个数与倒数第1个数,正数第2个数与倒数第2个数……他们有何关系?问题2:观察相邻两行数之间的关系,上一行数与下一行除1以外的数之间的关系。问题3:观察每一行中数的排列,有没有最大值?有没有单调性?问题4:观察每一行中数字之和,有什么规律?二项式系数的四个性质例题 、 证明在 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和. 小结:赋值法在二项式定理中,常对a,b赋予一些特 定的值1,-1等来整体得到所求。课堂练习: _ _ _ _ _ 变式训练:
1)已知 ,那么 = ;
2)1.研究斜行规律:第一条斜线上:第二条斜线上:第三条斜线上:第四条斜线上:猜想:在杨辉三角中,第m条斜线(从右上到左下)上前n个数字的和,等于1+1+1+1+1+1=61+2+3+4+5=151+3+6+10=201+4+10=15第m+1条斜线上的第n个数. 1+1+1+ ...+1= (第1条斜线 ) 1+4+10+ ...+ = (第4条斜线 ) 1+3+6+ ...+ = (第3条斜线 ) 1+2+3+ ...+ = (第2条斜线 ) (n>r) 125第5行 1 5 10 10 5 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第1行 1 1第0行 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1……1381321342.如图,写出斜线上各行数字的和,有什么规律?第8行 1 8 28 56 70 56 28 8 1 从第三个数起,任一数都等于前两个数的和;
这就是著名的斐波那契数列 。与数字11的幂的关系1 小结:二项式系数的四个性质布置作业:(1)课本第35-36页 探究与发现:
“杨辉三角”中的一些秘密;
(2)课本第35页练习:1、2、3题
《黄帝九章算法细草》《详解九章算法》
《日用算法》
《杨辉算法》
《乘除变通本末》
《算术三角形》
《思想录》Chinese triangle问题1:观察杨辉三角的每一行数字,正数第1个数与倒数第1个数,正数第2个数与倒数第2个数……他们有何关系?问题2:观察相邻两行数之间的关系,上一行数与下一行除1以外的数之间的关系。问题3:观察每一行中数的排列,有没有最大值?有没有单调性?问题4:观察每一行中数字之和,有什么规律?二项式系数的四个性质例题 、 证明在 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和. 小结:赋值法在二项式定理中,常对a,b赋予一些特 定的值1,-1等来整体得到所求。课堂练习: _ _ _ _ _ 变式训练:
1)已知 ,那么 = ;
2)1.研究斜行规律:第一条斜线上:第二条斜线上:第三条斜线上:第四条斜线上:猜想:在杨辉三角中,第m条斜线(从右上到左下)上前n个数字的和,等于1+1+1+1+1+1=61+2+3+4+5=151+3+6+10=201+4+10=15第m+1条斜线上的第n个数. 1+1+1+ ...+1= (第1条斜线 ) 1+4+10+ ...+ = (第4条斜线 ) 1+3+6+ ...+ = (第3条斜线 ) 1+2+3+ ...+ = (第2条斜线 ) (n>r) 125第5行 1 5 10 10 5 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第1行 1 1第0行 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1……1381321342.如图,写出斜线上各行数字的和,有什么规律?第8行 1 8 28 56 70 56 28 8 1 从第三个数起,任一数都等于前两个数的和;
这就是著名的斐波那契数列 。与数字11的幂的关系1 小结:二项式系数的四个性质布置作业:(1)课本第35-36页 探究与发现:
“杨辉三角”中的一些秘密;
(2)课本第35页练习:1、2、3题
