1.2.1 排列 课件(21张PPT)
文档属性
| 名称 | 1.2.1 排列 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 365.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:01:19 | ||
图片预览








文档简介
课件22张PPT。解排列问题的常用技巧 解排列问题的常用技巧 解排列问题,首先必须认真审题,明确问题是否是排列问题,其次是抓住问题的本质特征,灵活运用基本原理和公式进行分析解答,同时,还要注意讲究一些基本策略和方法技巧,使一些看似复杂的问题迎刃而解。
下面就不同的题型介绍几种常用的解题技巧。
总的原则—合理分类和准确分步 解排列(或)组合问题,应按元素的性质进行分类,事情的发生的连续过程分步,做到分类标准明确,分步层次清楚,不重不漏。解法1 分析:先安排甲,按照要求对其进行分类,分两类:根据分步及分类计数原理,不同的站法共有例1 6个同学和2个老师排成一排照相, 2个老师站中间,学生甲不站排头,学生乙不站排尾,共有多少种不同的排法?1)若甲在排尾上,则剩下的5人可自由安排,有 种方法.
若甲在第2、3、6、7位,则排尾的排法有 种,1位的排法有 种, 第2、3、6、7位的排法有 种,根据分步计数原理,不同的站法有 种。再安排老师,有2种方法。解法2 见练习3(2)(1)0,1,2,3,4,5可组成多少个无重复数字的五位偶数?个位数为零:个位数为2或4:所以练 习 1(2)0,1,2,3,4,5可组成多少个无重复数字且能被五整除的五位数?分类:后两位数字为5或0:个位数为0:个位数为5:(3)0,1,2,3,4,5可组成多少个无重复数字且大于31250的五位数?分类:(4)31250是由0,1,2,3,4,5组成的无重复数字的五位数中从小到大第几个数?方法一:(排除法)方法二:(直接法)(一)特殊元素的“优先安排法” 对于特殊元素的排列组合问题,一般应先考虑特殊元素,再考虑其它元素。 例2 用0,1,2,3,4这五个数,组成没有重复数字
的三位数,其中偶数共有( )
A.24 B.30 C.40 D.60 分析:由于该三位数是偶数,所以末尾数字必须是偶数, 又因为0不能排首位,故0就是其中的“特殊”元素,应优先安排。按0排在末尾和不排在末尾分为两类;0排在末尾时,有 个;
0不排在末尾时,先用偶数排个位,再排百位,最后排十位有 个;
由分类计数原理,共有偶数 30 个.B解题技巧 (1)0,1,2,3,4,5这六个数字可组成多少个无重复数字的五位数?(2)0,1,2,3,4,5可组成多少个无重复数字的五位奇数? 练 习 2 例3 用0,1,2,3,4这五个数,组成没有重复
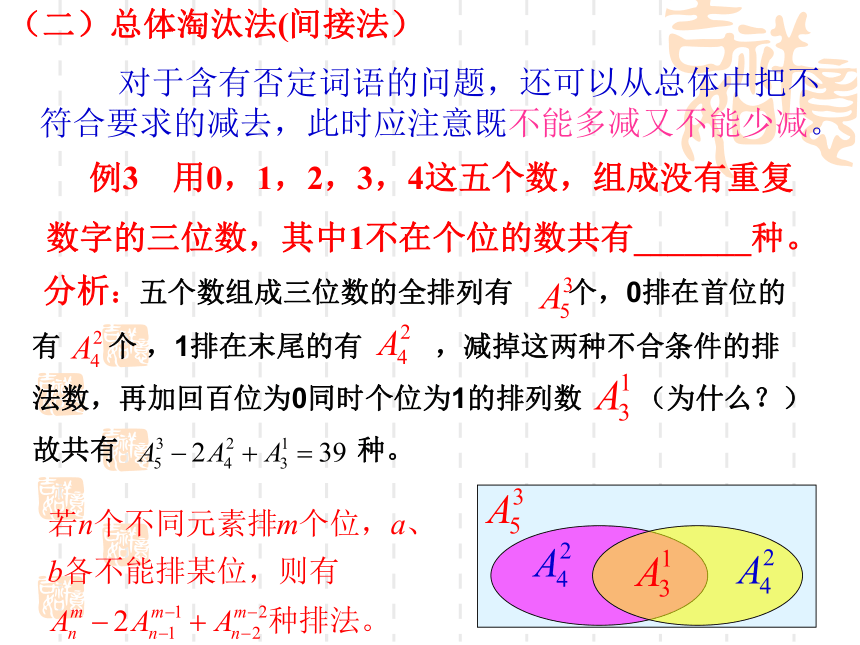
数字的三位数,其中1不在个位的数共有_______种。(二)总体淘汰法(间接法) 对于含有否定词语的问题,还可以从总体中把不符合要求的减去,此时应注意既不能多减又不能少减。 分析:五个数组成三位数的全排列有 个,0排在首位的
有 个 ,1排在末尾的有 ,减掉这两种不合条件的排
法数,再加回百位为0同时个位为1的排列数 (为什么?)
故共有 种。(1)三个男生,四个女生排成一排,甲不在最左,乙不在最右,有几种不同方法? (2)五人从左到右站成一排,其中甲不站排头,乙不站第二个位置,那么不同的站法有( )
A.120 B.96 C.78 D.72直接练 习 3 (3)0,1,2,3,4,5这六个数字可组成多少个无重复数字且个位数字不是4的五位数?(4)用间接法解例1—“6个同学和2个老师排成一排照相, 2个老师站中间,学生甲不站排头,学生乙不站排尾,共有多少种不同的排法?”(三)相邻问题——捆绑法 对于某几个元素要求相邻的排列问题,可先将相邻的元素“捆绑”在一起,看作一个“大”的元(组),与其它元素排列,然后再对相邻的元素(组)内部进行排列。例4 7人站成一排照相,要求甲,乙,丙三人相邻,分别有多少种站法?分析:先将甲,乙,丙三人捆绑在一起看作一个元素,与其余4人共有5个元素做全排列,有 种排法,然后对甲,乙,丙三人进行全排列。由分步计数原理可得:
种不同排法。(四)不相邻问题——插空法 对于某几个元素不相邻得排列问题,可先将其它
元素排好,然后再将不相邻的元素在已排好的元素
之间及两端的空隙之间插入即可。例5 7人站成一排照相,要求甲,乙,丙三人不相邻,分别有多少种站法?分析:可先让其余4人站好,共有 种排法,再在这4人之间及两端的5个“空隙”中选三个位置让甲、乙、丙插入,则有 种方法,这样共有 种不同的排法。(1)三个男生,四个女生排成一排,男生、女生各站一起,有几种不同方法?〈2〉三个男生,四个女生排成一排,男生之间、女生之间不相邻,有几种不同排法?捆绑法:插空法:〈3〉如果有两个男生、四个女生排成一排,要 求男生之间不相邻,有几种不同排法?插空法:练 习 4例6 有4名男生,3名女生。3名女生高矮互不等,
将7名学生排成一行,要求从左到右,女生从矮到高
排列,有多少种排法?(五)顺序固定问题用“除法” 对于某几个元素顺序一定的排列问题,可先将这几个元素与其它元素一同进行排列,然后用总的排列数除以这几个元素的全排列数.所以共有 种。 分析:先在7个位置上作全排列,有 种排法。其中
3个女生因要求“从矮到高”排,只有一种顺序故 只
对应一种排法,(1) 五人排队,甲在乙前面的排法有几种?练 习 5〈2〉三个男生,四个女生排成一排,其中甲、乙、丙三人的顺序不变,有几种不同排法?分析:若不考虑限制条件,则有 种排法,而甲,
乙之间排法有 种,故甲在乙前面的排法只有一种
符合条件,故
符合条件的排法有 种.(六)分排问题用“直排法” 把n个元素排成若干排的问题,若没有其他
的特殊要求,可采用统一排成一排的方法来处理.例7 七人坐两排座位,第一排坐3人,第二排坐
4人,则有多少种不同的坐法? 分析:7个人,可以在前后排随意就坐,再无
其他限制条件,故两排可看作一排处理,所以
不同的坐法有 种.(1)三个男生,四个女生排成两排,前排三人、后排四人,有几种不同排法?或:七个人可以在前后两排随意就坐,再无其他条件,
所以两排可看作一排来处理
不同的坐法有 种(2)八个人排成两排,有几种不同排法?练 习 6(七)实验法 题中附加条件增多,直接解决困难时,用实验逐步寻求规律有时也是行之有效的方法。 例8 将数字1,2,3,4填入标号为1,2,3,4的四个方格内,每个方格填1个,则每个方格的标号与所填的数字均不相同的填法种数有( )A.6 B.9 C.11 D.23分析:此题考查排列的定义,由于附加条件较多,解法较为困难,可用实验法逐步解决。第一方格内可填2或3或4。如填2,则第二方格中内可填1或3或4。若第二方格内填1,则第三方格只能填4,第四方格应填3。若第二方格内填3,则第三方格只能填4,第四方格应填1。同理,若第二方格内填4,则第三方格只能填1,第四方格应填3。因而,第一格填2有3种方法。不难得到,当第一格填3或4时也各有3种,所以共有9种。(八)住店法解决“允许重复排列问题”要注意区分两类元素: 一类元素可以重复,另一类不能重复,把不能重复的元素看作“客”,能重复的元素看作“店”,再利用乘法原理直接求解。例9 七名学生争夺五项冠军,每项冠军只能由一人获得,获得冠军的可能的种数有( )A. B. C D.分析:因同一学生可以同时夺得n项冠军,故学生可重复排列,将七名学生看作7家“店”,五项冠军看作5名“客”,每个“客”有7种住宿法,由乘法原理得 种。注:对此类问题,常有疑惑,为什么不是 呢?用分步计数原理看,5是步骤数,自然是指数。(九) 对应法例10 在100名选手之间进行单循环淘汰赛(即一场
比赛失败要退出比赛),最后产生一名冠军,问要
举行几场? 分析:要产生一名冠军,需要淘汰掉冠军以外的
所有选手,即要淘汰99名选手,淘汰一名选手需要
进行一场比赛,所以淘汰99名选手就需要99场比赛。(十)特征分析 研究有约束条件的排数问题,须要紧扣题目所提供的数字特征,结构特征,进行推理,分析求解。 例11 由1,2,3,4,5,6六个数字可以组成多少个无重复且是6的倍数的五位数?分析数字特征:6的倍数既是2的倍数又是3的倍数。其中3的倍数又满足“各个数位上的数字之和是3的倍数”的特征。把6分成4组,(3,3),(6),(1,5),(2,4),每组的数字和都是3的倍数。因此可分成两类讨论;第一类:由1,2,4,5,6作数码;首先从2,4,6中任选一个作个位数字有 ,然后其余四个数在其他数位上全排列有 ,所以第二类:由1,2,3,4,5作数码。依上法有(1)三个男生,四个女生排成一排,甲不能在中间,也不在两头,有几种不同方法?(2)三个男生,四个女生排成一排,甲只能在中间或两头,有几种不同排法?找位置:找位置:练 习 7
下面就不同的题型介绍几种常用的解题技巧。
总的原则—合理分类和准确分步 解排列(或)组合问题,应按元素的性质进行分类,事情的发生的连续过程分步,做到分类标准明确,分步层次清楚,不重不漏。解法1 分析:先安排甲,按照要求对其进行分类,分两类:根据分步及分类计数原理,不同的站法共有例1 6个同学和2个老师排成一排照相, 2个老师站中间,学生甲不站排头,学生乙不站排尾,共有多少种不同的排法?1)若甲在排尾上,则剩下的5人可自由安排,有 种方法.
若甲在第2、3、6、7位,则排尾的排法有 种,1位的排法有 种, 第2、3、6、7位的排法有 种,根据分步计数原理,不同的站法有 种。再安排老师,有2种方法。解法2 见练习3(2)(1)0,1,2,3,4,5可组成多少个无重复数字的五位偶数?个位数为零:个位数为2或4:所以练 习 1(2)0,1,2,3,4,5可组成多少个无重复数字且能被五整除的五位数?分类:后两位数字为5或0:个位数为0:个位数为5:(3)0,1,2,3,4,5可组成多少个无重复数字且大于31250的五位数?分类:(4)31250是由0,1,2,3,4,5组成的无重复数字的五位数中从小到大第几个数?方法一:(排除法)方法二:(直接法)(一)特殊元素的“优先安排法” 对于特殊元素的排列组合问题,一般应先考虑特殊元素,再考虑其它元素。 例2 用0,1,2,3,4这五个数,组成没有重复数字
的三位数,其中偶数共有( )
A.24 B.30 C.40 D.60 分析:由于该三位数是偶数,所以末尾数字必须是偶数, 又因为0不能排首位,故0就是其中的“特殊”元素,应优先安排。按0排在末尾和不排在末尾分为两类;0排在末尾时,有 个;
0不排在末尾时,先用偶数排个位,再排百位,最后排十位有 个;
由分类计数原理,共有偶数 30 个.B解题技巧 (1)0,1,2,3,4,5这六个数字可组成多少个无重复数字的五位数?(2)0,1,2,3,4,5可组成多少个无重复数字的五位奇数? 练 习 2 例3 用0,1,2,3,4这五个数,组成没有重复
数字的三位数,其中1不在个位的数共有_______种。(二)总体淘汰法(间接法) 对于含有否定词语的问题,还可以从总体中把不符合要求的减去,此时应注意既不能多减又不能少减。 分析:五个数组成三位数的全排列有 个,0排在首位的
有 个 ,1排在末尾的有 ,减掉这两种不合条件的排
法数,再加回百位为0同时个位为1的排列数 (为什么?)
故共有 种。(1)三个男生,四个女生排成一排,甲不在最左,乙不在最右,有几种不同方法? (2)五人从左到右站成一排,其中甲不站排头,乙不站第二个位置,那么不同的站法有( )
A.120 B.96 C.78 D.72直接练 习 3 (3)0,1,2,3,4,5这六个数字可组成多少个无重复数字且个位数字不是4的五位数?(4)用间接法解例1—“6个同学和2个老师排成一排照相, 2个老师站中间,学生甲不站排头,学生乙不站排尾,共有多少种不同的排法?”(三)相邻问题——捆绑法 对于某几个元素要求相邻的排列问题,可先将相邻的元素“捆绑”在一起,看作一个“大”的元(组),与其它元素排列,然后再对相邻的元素(组)内部进行排列。例4 7人站成一排照相,要求甲,乙,丙三人相邻,分别有多少种站法?分析:先将甲,乙,丙三人捆绑在一起看作一个元素,与其余4人共有5个元素做全排列,有 种排法,然后对甲,乙,丙三人进行全排列。由分步计数原理可得:
种不同排法。(四)不相邻问题——插空法 对于某几个元素不相邻得排列问题,可先将其它
元素排好,然后再将不相邻的元素在已排好的元素
之间及两端的空隙之间插入即可。例5 7人站成一排照相,要求甲,乙,丙三人不相邻,分别有多少种站法?分析:可先让其余4人站好,共有 种排法,再在这4人之间及两端的5个“空隙”中选三个位置让甲、乙、丙插入,则有 种方法,这样共有 种不同的排法。(1)三个男生,四个女生排成一排,男生、女生各站一起,有几种不同方法?〈2〉三个男生,四个女生排成一排,男生之间、女生之间不相邻,有几种不同排法?捆绑法:插空法:〈3〉如果有两个男生、四个女生排成一排,要 求男生之间不相邻,有几种不同排法?插空法:练 习 4例6 有4名男生,3名女生。3名女生高矮互不等,
将7名学生排成一行,要求从左到右,女生从矮到高
排列,有多少种排法?(五)顺序固定问题用“除法” 对于某几个元素顺序一定的排列问题,可先将这几个元素与其它元素一同进行排列,然后用总的排列数除以这几个元素的全排列数.所以共有 种。 分析:先在7个位置上作全排列,有 种排法。其中
3个女生因要求“从矮到高”排,只有一种顺序故 只
对应一种排法,(1) 五人排队,甲在乙前面的排法有几种?练 习 5〈2〉三个男生,四个女生排成一排,其中甲、乙、丙三人的顺序不变,有几种不同排法?分析:若不考虑限制条件,则有 种排法,而甲,
乙之间排法有 种,故甲在乙前面的排法只有一种
符合条件,故
符合条件的排法有 种.(六)分排问题用“直排法” 把n个元素排成若干排的问题,若没有其他
的特殊要求,可采用统一排成一排的方法来处理.例7 七人坐两排座位,第一排坐3人,第二排坐
4人,则有多少种不同的坐法? 分析:7个人,可以在前后排随意就坐,再无
其他限制条件,故两排可看作一排处理,所以
不同的坐法有 种.(1)三个男生,四个女生排成两排,前排三人、后排四人,有几种不同排法?或:七个人可以在前后两排随意就坐,再无其他条件,
所以两排可看作一排来处理
不同的坐法有 种(2)八个人排成两排,有几种不同排法?练 习 6(七)实验法 题中附加条件增多,直接解决困难时,用实验逐步寻求规律有时也是行之有效的方法。 例8 将数字1,2,3,4填入标号为1,2,3,4的四个方格内,每个方格填1个,则每个方格的标号与所填的数字均不相同的填法种数有( )A.6 B.9 C.11 D.23分析:此题考查排列的定义,由于附加条件较多,解法较为困难,可用实验法逐步解决。第一方格内可填2或3或4。如填2,则第二方格中内可填1或3或4。若第二方格内填1,则第三方格只能填4,第四方格应填3。若第二方格内填3,则第三方格只能填4,第四方格应填1。同理,若第二方格内填4,则第三方格只能填1,第四方格应填3。因而,第一格填2有3种方法。不难得到,当第一格填3或4时也各有3种,所以共有9种。(八)住店法解决“允许重复排列问题”要注意区分两类元素: 一类元素可以重复,另一类不能重复,把不能重复的元素看作“客”,能重复的元素看作“店”,再利用乘法原理直接求解。例9 七名学生争夺五项冠军,每项冠军只能由一人获得,获得冠军的可能的种数有( )A. B. C D.分析:因同一学生可以同时夺得n项冠军,故学生可重复排列,将七名学生看作7家“店”,五项冠军看作5名“客”,每个“客”有7种住宿法,由乘法原理得 种。注:对此类问题,常有疑惑,为什么不是 呢?用分步计数原理看,5是步骤数,自然是指数。(九) 对应法例10 在100名选手之间进行单循环淘汰赛(即一场
比赛失败要退出比赛),最后产生一名冠军,问要
举行几场? 分析:要产生一名冠军,需要淘汰掉冠军以外的
所有选手,即要淘汰99名选手,淘汰一名选手需要
进行一场比赛,所以淘汰99名选手就需要99场比赛。(十)特征分析 研究有约束条件的排数问题,须要紧扣题目所提供的数字特征,结构特征,进行推理,分析求解。 例11 由1,2,3,4,5,6六个数字可以组成多少个无重复且是6的倍数的五位数?分析数字特征:6的倍数既是2的倍数又是3的倍数。其中3的倍数又满足“各个数位上的数字之和是3的倍数”的特征。把6分成4组,(3,3),(6),(1,5),(2,4),每组的数字和都是3的倍数。因此可分成两类讨论;第一类:由1,2,4,5,6作数码;首先从2,4,6中任选一个作个位数字有 ,然后其余四个数在其他数位上全排列有 ,所以第二类:由1,2,3,4,5作数码。依上法有(1)三个男生,四个女生排成一排,甲不能在中间,也不在两头,有几种不同方法?(2)三个男生,四个女生排成一排,甲只能在中间或两头,有几种不同排法?找位置:找位置:练 习 7
