1.3.2 杨辉三角 课件(22张PPT)
文档属性
| 名称 | 1.3.2 杨辉三角 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览







文档简介
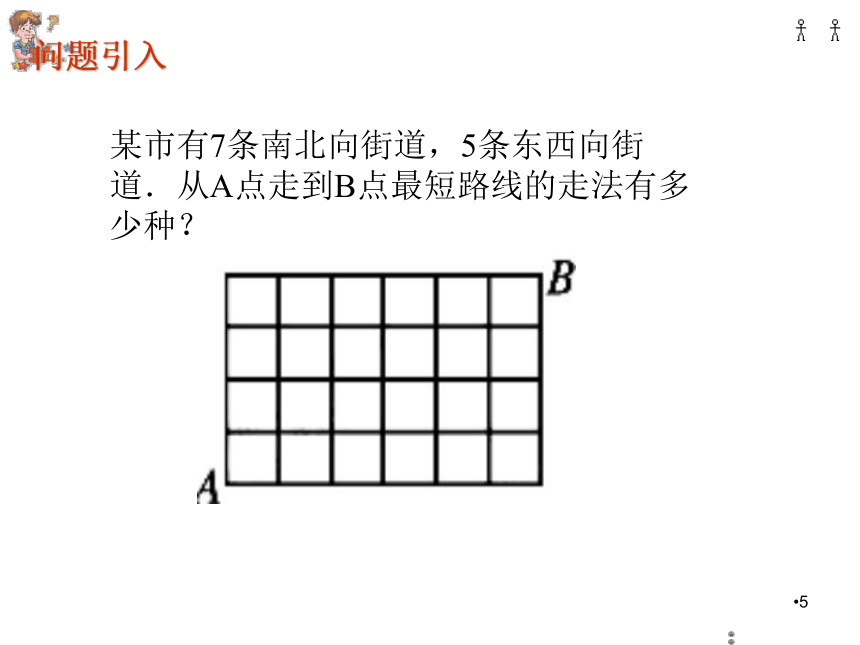
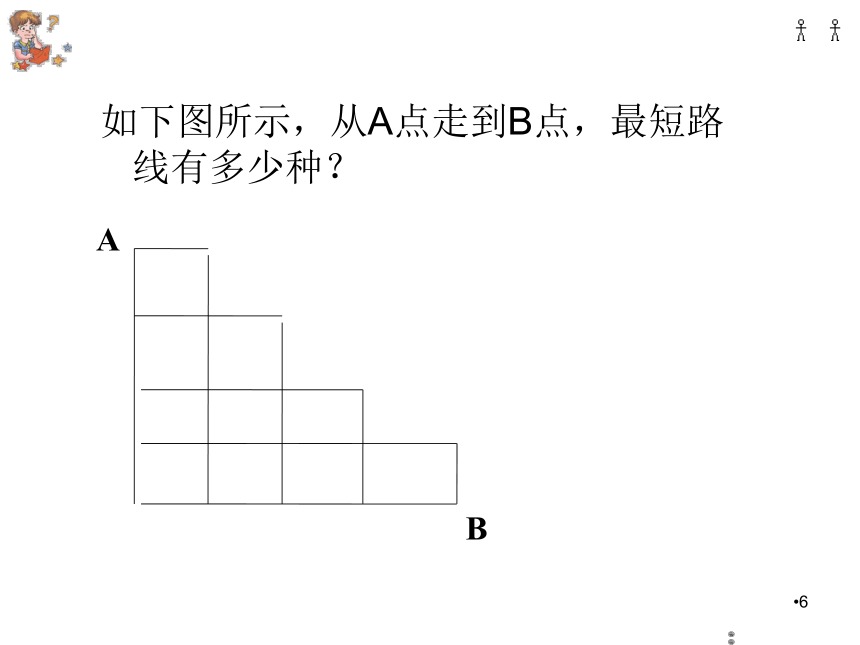
课件22张PPT。 (选修2-3)第一章 计数原理1.3.2 “杨辉三角”与二项式系数的性质5(见例3)问题引入某市有7条南北向街道,5条东西向街道.从A点走到B点最短路线的走法有多少种?6如下图所示,从A点走到B点,最短路线有多少种?BA7组合数性质:复习关键点二项式定理:二项式系数依次是:二项式系数的性质?9探究规律杨辉三角的介绍详解九章算法杨 辉杨辉三角的介绍法国数学家——帕斯克公元十一世纪1653年北宋数学家——贾宪早500年
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 113一三四六五十一一二一一三一一四一一五十一一总结规律14一三四六五十一一二一一三一一四一一五十一一杨辉三角f(r)=探究规律15特殊观察f(r)=16(3)二项式系数的增减性: 如果二项式的幂指数是偶数,则中间一项的二项式系数最大; 如果二项式的幂指数是奇数,则中间两项的二项式系数相等,且同时取得最大值;TTT总结规律17成果验收18(见例3)问题引入某市有7条南北向街道,5条东西向街道.从A点走到B点最短路线的走法有多少种?DCGHMKMFE19如下图所示,从A点走到B点,最短路线有多少种?BA11112345215914514281442cvefghnmsq0klpzju20课堂小结⑴二项式系数的对称性: 在二项展开式中,与首末两端“等距离”的两项的二项式系数相等;⑵二项式系数的增减性: 如果二项式的幂指数是偶数,则中间一项的二项式系数最大; 如果二项式的幂指数是奇数,则中间两项的二项式系数相等,且同时取得最大值.TTT你又掌握了哪些数学思想方法?
由特殊到一般
由一般到特殊
归纳推理
函数思想
22课后再做好复习巩固.
谢谢!再见!
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 113一三四六五十一一二一一三一一四一一五十一一总结规律14一三四六五十一一二一一三一一四一一五十一一杨辉三角f(r)=探究规律15特殊观察f(r)=16(3)二项式系数的增减性: 如果二项式的幂指数是偶数,则中间一项的二项式系数最大; 如果二项式的幂指数是奇数,则中间两项的二项式系数相等,且同时取得最大值;TTT总结规律17成果验收18(见例3)问题引入某市有7条南北向街道,5条东西向街道.从A点走到B点最短路线的走法有多少种?DCGHMKMFE19如下图所示,从A点走到B点,最短路线有多少种?BA11112345215914514281442cvefghnmsq0klpzju20课堂小结⑴二项式系数的对称性: 在二项展开式中,与首末两端“等距离”的两项的二项式系数相等;⑵二项式系数的增减性: 如果二项式的幂指数是偶数,则中间一项的二项式系数最大; 如果二项式的幂指数是奇数,则中间两项的二项式系数相等,且同时取得最大值.TTT你又掌握了哪些数学思想方法?
由特殊到一般
由一般到特殊
归纳推理
函数思想
22课后再做好复习巩固.
谢谢!再见!
