2.1.2 离散型随机变量的分布列 课件(20张PPT)
文档属性
| 名称 | 2.1.2 离散型随机变量的分布列 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 654.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:19:15 | ||
图片预览





文档简介
课件20张PPT。离散型随机变量的分布列人教B版/数学选修2-3/2.1.2 (1)随机变量的含义是什么?环节一
复习旧知如果随机试验的结果可以用一个变量来X表示,且X是随着实验结果的不同而变化的,那么这样的变量叫做随机变量。离散型随机变量和连续型随机变量(2)随机变量分为哪两类?(3)离散型随机变量的定义?对于随机变量可能取的值都能一一列举出来,这样的随机变量叫做离散型随机变量。(4)互斥事件的概率加法公式是怎样的?学习目标1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;
2、掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单问题;
3、理解二点分布的概念。引例1:抛掷一枚骰子,设得到的点数为ξ,则ξ可能取的值有:1,2,3,4,5,6.由概率知识可知,ξ取各值的概率都等于此表从概率的角度指出了随机变量在随机试验中取值的分布情况,称为随机变量ξ的概率分布.环节二
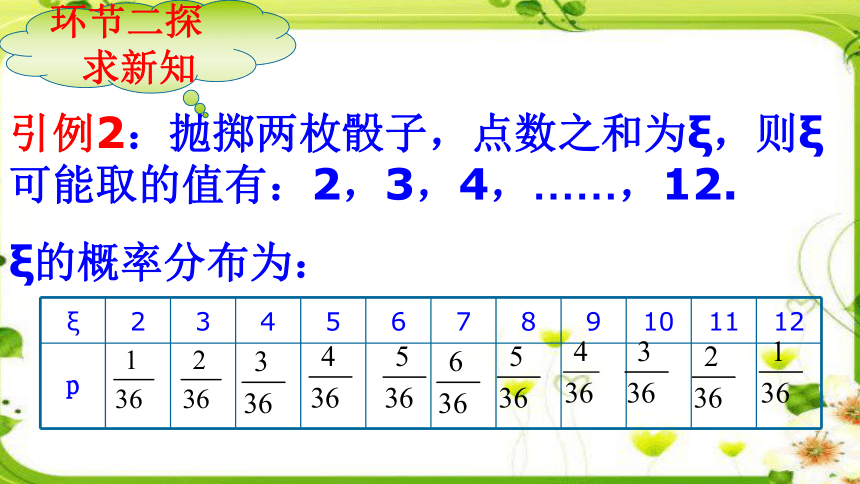
探求新知引例2:抛掷两枚骰子,点数之和为ξ,则ξ可能取的值有:2,3,4,……,12.
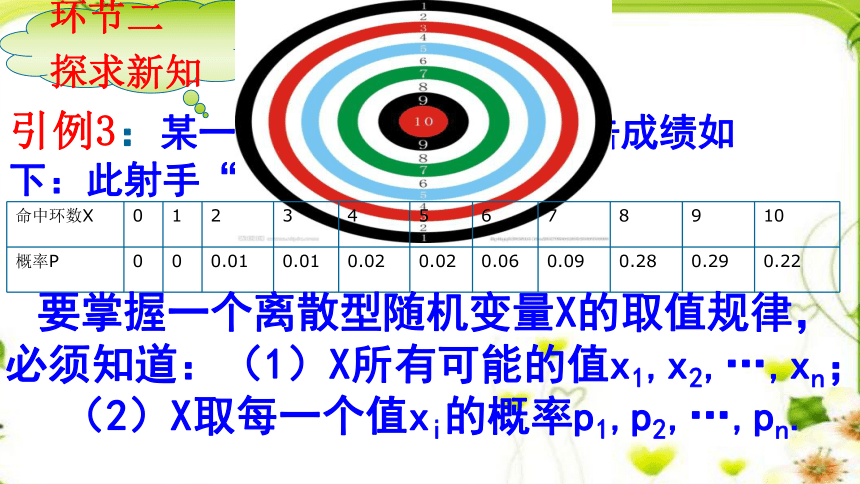
ξ的概率分布为:环节二探求新知引例3:某一射手在一段时间的射击成绩如下:此射手“射击水平如何”?环节二
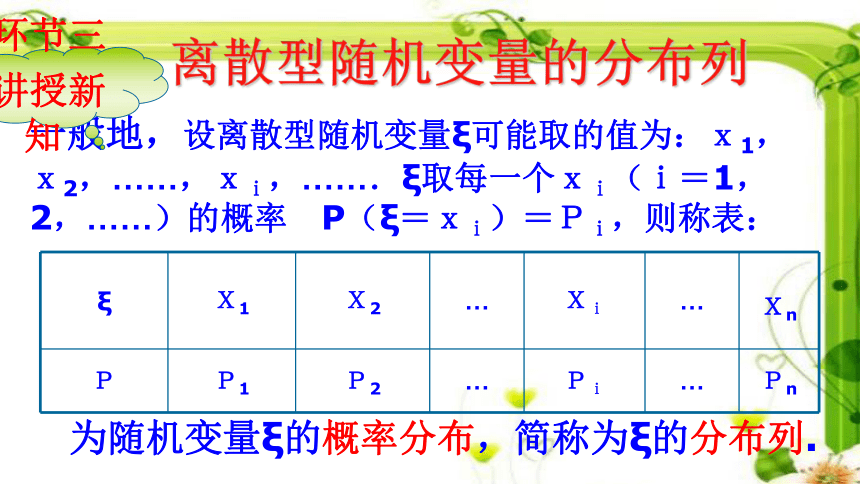
探求新知要掌握一个离散型随机变量X的取值规律,必须知道:(1)X所有可能的值x1,x2,…,xn;(2)X取每一个值xi的概率p1,p2,…,pn.一般地,设离散型随机变量ξ可能取的值为:x1,x2,……,xi,…….ξ取每一个xi(i=1,2,……)的概率 P(ξ=xi)=Pi,则称表:为随机变量ξ的概率分布,简称为ξ的分布列.离散型随机变量的分布列环节三
讲授新知(1)Pi≥0,i=1,2,……;
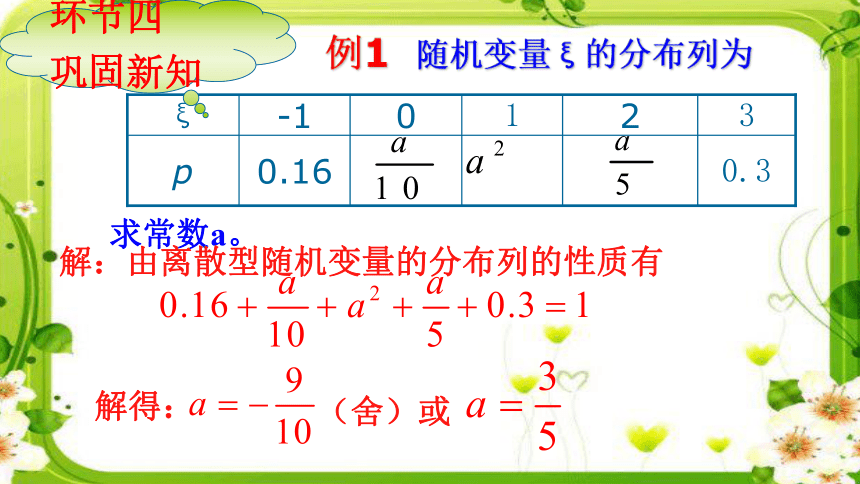
(2)P1+P2+……=1离散型随机变量的分布列的两个性质:例1 随机变量ξ的分布列为求常数a。解:由离散型随机变量的分布列的性质有解得:(舍)或环节四
巩固新知变式:已知随机变量X只能取三个值x1,x2,x3,其概率值依次成等差数列,求公差d的取值范围解:分布列为:例题2.篮球运动员在比赛中每罚球命中得1分,罚不中得0分。已知某运动员罚球命中的概率为0.7,求他罚球1次的得分的分布列。解:该篮球运动员罚球1次的得分的分布列为:ξP010.30.7环节四
巩固新知解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:二点分布如果随机变量X的分布列为其中0>p >1,q=1-p,则称离散型随机变量X服从参数为p的二点分布 注:二点分布是最简单的一种分布,任何一个只有两种可能结果的随机现象, 比如新生婴儿是男还是女、明天是否下雨、种籽是否发芽等, 都属于二点分布.环节三
讲授新知例题3、掷一颗骰子,所掷出的点数为随机变量X:(1)求X的分布列;(2)求“点数大于4”的概率;
(3)求“点数不超过5”的概率
环节四
巩固新知解:见黑板板书 ☆求分布列重在过程,必须有文字说明和详细过程,切忌只有数、式或表!环节四
巩固新知例题4一个口袋里有5只球,编号为1,2,3,4,5,
在袋中同时取出3只,以ξ表示取出的3个球中
的最小号码,试写出ξ的分布列. 解: 随机变量ξ的取值为 1,2,3.ξ=1表示最小号码为1,另两个号码从余下的4个号码
中选,有C42种选法,又共有C52种选法,且等可能.故P(ξ=1)= C42/ C52 =3/5;同理可得 P(ξ=2)=3/10;P(ξ=3)=1/10. 因此,ξ的分布列如下表所示环节四
巩固新知思考:求随机变量的分布列的主要步骤(1)明确随机变量的表示的含义,列出所有取值。(2)求每一个随机变量取值的概率;(可用古典概型的求法)(3)列成表格.环节四
巩固新知变式:解 由题意,所给分布列为
小结:主要内容1、离散型随机变量的分布列的意义,
2 、求离散型随机变量的分布列的步骤;
3、应用离散型随机变量的分布列的两个基本性质,解决一些简单问题;
4、理解二点分布的概念。当堂检测:见导学案课后作业:见拓展案
复习旧知如果随机试验的结果可以用一个变量来X表示,且X是随着实验结果的不同而变化的,那么这样的变量叫做随机变量。离散型随机变量和连续型随机变量(2)随机变量分为哪两类?(3)离散型随机变量的定义?对于随机变量可能取的值都能一一列举出来,这样的随机变量叫做离散型随机变量。(4)互斥事件的概率加法公式是怎样的?学习目标1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;
2、掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单问题;
3、理解二点分布的概念。引例1:抛掷一枚骰子,设得到的点数为ξ,则ξ可能取的值有:1,2,3,4,5,6.由概率知识可知,ξ取各值的概率都等于此表从概率的角度指出了随机变量在随机试验中取值的分布情况,称为随机变量ξ的概率分布.环节二
探求新知引例2:抛掷两枚骰子,点数之和为ξ,则ξ可能取的值有:2,3,4,……,12.
ξ的概率分布为:环节二探求新知引例3:某一射手在一段时间的射击成绩如下:此射手“射击水平如何”?环节二
探求新知要掌握一个离散型随机变量X的取值规律,必须知道:(1)X所有可能的值x1,x2,…,xn;(2)X取每一个值xi的概率p1,p2,…,pn.一般地,设离散型随机变量ξ可能取的值为:x1,x2,……,xi,…….ξ取每一个xi(i=1,2,……)的概率 P(ξ=xi)=Pi,则称表:为随机变量ξ的概率分布,简称为ξ的分布列.离散型随机变量的分布列环节三
讲授新知(1)Pi≥0,i=1,2,……;
(2)P1+P2+……=1离散型随机变量的分布列的两个性质:例1 随机变量ξ的分布列为求常数a。解:由离散型随机变量的分布列的性质有解得:(舍)或环节四
巩固新知变式:已知随机变量X只能取三个值x1,x2,x3,其概率值依次成等差数列,求公差d的取值范围解:分布列为:例题2.篮球运动员在比赛中每罚球命中得1分,罚不中得0分。已知某运动员罚球命中的概率为0.7,求他罚球1次的得分的分布列。解:该篮球运动员罚球1次的得分的分布列为:ξP010.30.7环节四
巩固新知解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:二点分布如果随机变量X的分布列为其中0>p >1,q=1-p,则称离散型随机变量X服从参数为p的二点分布 注:二点分布是最简单的一种分布,任何一个只有两种可能结果的随机现象, 比如新生婴儿是男还是女、明天是否下雨、种籽是否发芽等, 都属于二点分布.环节三
讲授新知例题3、掷一颗骰子,所掷出的点数为随机变量X:(1)求X的分布列;(2)求“点数大于4”的概率;
(3)求“点数不超过5”的概率
环节四
巩固新知解:见黑板板书 ☆求分布列重在过程,必须有文字说明和详细过程,切忌只有数、式或表!环节四
巩固新知例题4一个口袋里有5只球,编号为1,2,3,4,5,
在袋中同时取出3只,以ξ表示取出的3个球中
的最小号码,试写出ξ的分布列. 解: 随机变量ξ的取值为 1,2,3.ξ=1表示最小号码为1,另两个号码从余下的4个号码
中选,有C42种选法,又共有C52种选法,且等可能.故P(ξ=1)= C42/ C52 =3/5;同理可得 P(ξ=2)=3/10;P(ξ=3)=1/10. 因此,ξ的分布列如下表所示环节四
巩固新知思考:求随机变量的分布列的主要步骤(1)明确随机变量的表示的含义,列出所有取值。(2)求每一个随机变量取值的概率;(可用古典概型的求法)(3)列成表格.环节四
巩固新知变式:解 由题意,所给分布列为
小结:主要内容1、离散型随机变量的分布列的意义,
2 、求离散型随机变量的分布列的步骤;
3、应用离散型随机变量的分布列的两个基本性质,解决一些简单问题;
4、理解二点分布的概念。当堂检测:见导学案课后作业:见拓展案
