2.1.2 离散型随机变量的分布列 课件(20张PPT)
文档属性
| 名称 | 2.1.2 离散型随机变量的分布列 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览








文档简介
课件20张PPT。贵定中学教师:程勇2.1.2离散型随机变量的分布列2.1.2离散型随机变量的分布列
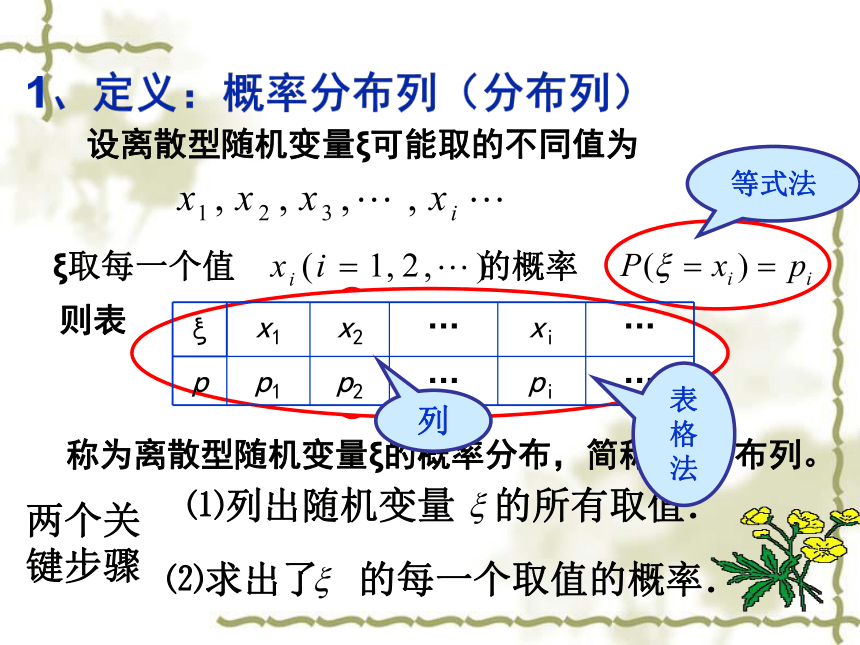
一、复习回顾: 随机变量: 如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量常用希腊字母X、Y、ξ、η表示。离散型随机变量: 对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。学习目标:1)理解离散型随机变量分布列的意义,会求某些简单的离散型随机变量的分布列。2)掌握离散型随机变量分布列的两个基本性质,并会用它来解决一些简单的问题.3)掌握两点分布及其相关的应用引例:抛掷一个骰子的随机试验中,设得到的点数为ξ,则ξ的取值情况如何? ξ取各个值的概率分别是什么?解:列 表:二、离散型随机变量的分布列表中从概率的角度指出了随机变量在随机试验中取值的分布状况,称为随机变量的概率分布列。称为离散型随机变量ξ的概率分布,简称ξ的分布列。则表设离散型随机变量ξ可能取的不同值为1、定义:概率分布列(分布列)两个关
键步骤⑴列出随机变量 的所有取值. ⑵求出了 的每一个取值的概率.等式法表格法列2、分布列的表示法2)解析式法表示: 3)用图象法表示:PX01函数用解析式、表格法、图象法1)列表法:3.分布列的性质:注:这个两个性质是判断分布列是否正确的重要依据例如:某同学求得一离散型随机变量的分布列如下:试说明该同学的计算结果是否正确? 根据射手射击所得环数ξ的分布列,有例1、某一射手射击所得环数ξ的分布列如下:求此射手” ≥7”的概率. 分析: “ ≥7”的事件有哪些? 解:P(ξ=7)=0.09,P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22,所求的概率为P(ξ≥7)=0.09+ 0.28+ 0.29+ 0.22= 0.88三、沙场点兵 小结:一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。例2、随机变量ξ的分布列为1)求常数 a;解:1)由离散型随机变量的分布列的性质有:2)例3、连续抛掷两个骰子,得到的点数之和为ξ,
则ξ取哪些值?求ξ的概率分布列?解:的可能取值有:2、3、4、5、6、7、8、
9、10、11、12由古典概型计算出各取值的概率得到分布列为:求离散型随机变量的分布列步骤:S1:求出 的所有可能取值S2:求出 取值各个值的概率 S3:列出分布列解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:3、两点分布列象上面这样的分布列称为两点分布列。如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。练习:1、在射击的随机试验中,令X= 如
果射中的概率为0.8,求随机变量X的分布列。0,射中,
1,未射中4.设随机变量 的分布列为则 的值为 .3.设随机变量 的分布列如下:4321则 的值为 .5.设随机变量 的分布列为则 ( )A、1B、C、D、6.设随机变量 只能取5、6、7、···、16这12个值,且取每一个值的概率均相等,则 ,
D小结:1.随机变量的分布列:2、分布列的性质:3、求分布列的步骤:4. 两点分布作业:课本P49 习题第1题, A组5题 且相应取值的概率没有变化思考:已知随机变量 的分布列如下:-2-13210分别求出随机变量⑴;⑵的分布列.:已知随机变量 的分布列如下:-2-13210分别求出随机变量⑴;⑵的分布列.再见再见
一、复习回顾: 随机变量: 如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量常用希腊字母X、Y、ξ、η表示。离散型随机变量: 对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。学习目标:1)理解离散型随机变量分布列的意义,会求某些简单的离散型随机变量的分布列。2)掌握离散型随机变量分布列的两个基本性质,并会用它来解决一些简单的问题.3)掌握两点分布及其相关的应用引例:抛掷一个骰子的随机试验中,设得到的点数为ξ,则ξ的取值情况如何? ξ取各个值的概率分别是什么?解:列 表:二、离散型随机变量的分布列表中从概率的角度指出了随机变量在随机试验中取值的分布状况,称为随机变量的概率分布列。称为离散型随机变量ξ的概率分布,简称ξ的分布列。则表设离散型随机变量ξ可能取的不同值为1、定义:概率分布列(分布列)两个关
键步骤⑴列出随机变量 的所有取值. ⑵求出了 的每一个取值的概率.等式法表格法列2、分布列的表示法2)解析式法表示: 3)用图象法表示:PX01函数用解析式、表格法、图象法1)列表法:3.分布列的性质:注:这个两个性质是判断分布列是否正确的重要依据例如:某同学求得一离散型随机变量的分布列如下:试说明该同学的计算结果是否正确? 根据射手射击所得环数ξ的分布列,有例1、某一射手射击所得环数ξ的分布列如下:求此射手” ≥7”的概率. 分析: “ ≥7”的事件有哪些? 解:P(ξ=7)=0.09,P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22,所求的概率为P(ξ≥7)=0.09+ 0.28+ 0.29+ 0.22= 0.88三、沙场点兵 小结:一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。例2、随机变量ξ的分布列为1)求常数 a;解:1)由离散型随机变量的分布列的性质有:2)例3、连续抛掷两个骰子,得到的点数之和为ξ,
则ξ取哪些值?求ξ的概率分布列?解:的可能取值有:2、3、4、5、6、7、8、
9、10、11、12由古典概型计算出各取值的概率得到分布列为:求离散型随机变量的分布列步骤:S1:求出 的所有可能取值S2:求出 取值各个值的概率 S3:列出分布列解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:3、两点分布列象上面这样的分布列称为两点分布列。如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。练习:1、在射击的随机试验中,令X= 如
果射中的概率为0.8,求随机变量X的分布列。0,射中,
1,未射中4.设随机变量 的分布列为则 的值为 .3.设随机变量 的分布列如下:4321则 的值为 .5.设随机变量 的分布列为则 ( )A、1B、C、D、6.设随机变量 只能取5、6、7、···、16这12个值,且取每一个值的概率均相等,则 ,
D小结:1.随机变量的分布列:2、分布列的性质:3、求分布列的步骤:4. 两点分布作业:课本P49 习题第1题, A组5题 且相应取值的概率没有变化思考:已知随机变量 的分布列如下:-2-13210分别求出随机变量⑴;⑵的分布列.:已知随机变量 的分布列如下:-2-13210分别求出随机变量⑴;⑵的分布列.再见再见
