2.3.1 离散型随机变量的数学期望 课件(20张PPT)
文档属性
| 名称 | 2.3.1 离散型随机变量的数学期望 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:21:46 | ||
图片预览








文档简介
课件20张PPT。第二章 随机变量及其分布列1、离散型随机变量的分布列2、离散型随机变量分布列的性质:(1)pi≥0,i=1,2,…;
(2)p1+p2+…+pi+…=1. 温故知新 对于离散型随机变量,可以由它的概率分布列确定与该随机变量相关事件的概率。但在实际问题中,有时我们更感兴趣的是随机变量的某些数字特征。例如,要了解某班同学在一次数学测验中的总体水平,很重要的是看平均分;要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。
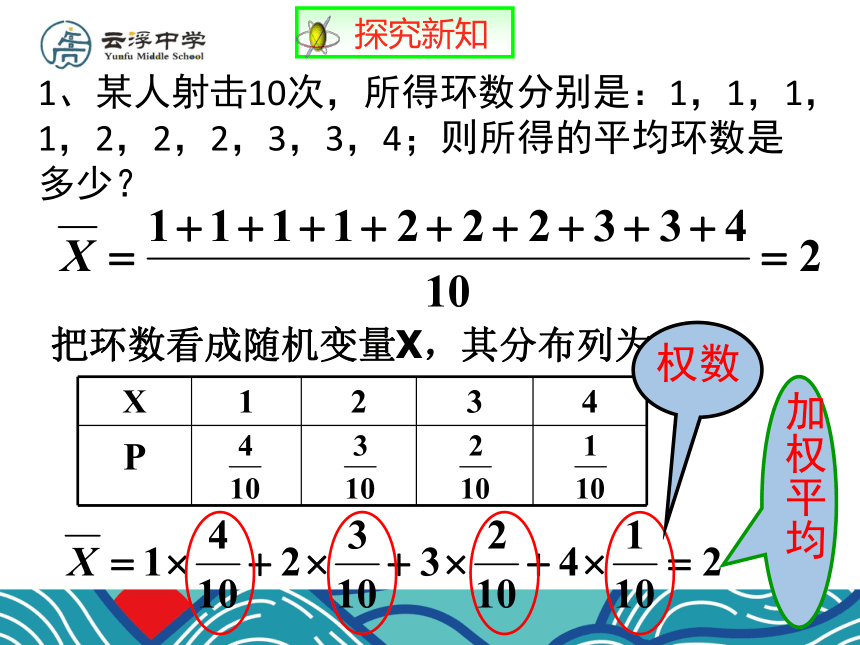
我们还常常希望直接通过数字来反映随机变量的某个方面的特征,最常用的有均值与方差.2.3.1离散型随机变量的均值 1、某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?把环数看成随机变量X,其分布列为:权数加权平均 探究新知2、某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?把3种糖果的价格看成随机变量X,其分布列为:一、离散型随机变量取值的平均值数学期望一般地,若离散型随机变量X的分布列为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。 概念解析设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1)Y的分布列是什么?
(2)E(Y)=?思考:······························一、离散型随机变量取值的平均值数学期望二、数学期望的性质1、随机变量ξ的分布列是(1)则Eξ= . 2.4(2)若η=2ξ+1,则Eη= . 5.8 小试牛刀2、随机变量ξ的分布列是Eξ=7.5,则a= b= .0.10.4例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则小结: 例题解析例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;(1)求他得到的分数X的分布列;(2)求X的期望。解:(1)因为 X~B(3,0.7),
所以P(x=k)= (k=0,1,2,3)(2)一般地,如果随机变量X服从二项分布,即X~B(n,p),则基础训练: 一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .3 总结升华1.一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且只有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分,学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的成绩的期望。 跟踪训练2、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。(保留三个有效数字)E =1.43一、离散型随机变量取值的平均值数学期望二、数学期望的性质 课堂小结三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则 作 业 P68/习题2.3/A组/2,3
(2)p1+p2+…+pi+…=1. 温故知新 对于离散型随机变量,可以由它的概率分布列确定与该随机变量相关事件的概率。但在实际问题中,有时我们更感兴趣的是随机变量的某些数字特征。例如,要了解某班同学在一次数学测验中的总体水平,很重要的是看平均分;要了解某班同学数学成绩是否“两极分化”则需要考察这个班数学成绩的方差。
我们还常常希望直接通过数字来反映随机变量的某个方面的特征,最常用的有均值与方差.2.3.1离散型随机变量的均值 1、某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?把环数看成随机变量X,其分布列为:权数加权平均 探究新知2、某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?把3种糖果的价格看成随机变量X,其分布列为:一、离散型随机变量取值的平均值数学期望一般地,若离散型随机变量X的分布列为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。 概念解析设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1)Y的分布列是什么?
(2)E(Y)=?思考:······························一、离散型随机变量取值的平均值数学期望二、数学期望的性质1、随机变量ξ的分布列是(1)则Eξ= . 2.4(2)若η=2ξ+1,则Eη= . 5.8 小试牛刀2、随机变量ξ的分布列是Eξ=7.5,则a= b= .0.10.4例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则小结: 例题解析例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;(1)求他得到的分数X的分布列;(2)求X的期望。解:(1)因为 X~B(3,0.7),
所以P(x=k)= (k=0,1,2,3)(2)一般地,如果随机变量X服从二项分布,即X~B(n,p),则基础训练: 一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .3 总结升华1.一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且只有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分,学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和乙在这次英语单元测验中的成绩的期望。 跟踪训练2、射手用手枪进行射击,击中目标就停止,否则继续射击,他射中目标的概率是0.7,若枪内只有5颗子弹,求射击次数的期望。(保留三个有效数字)E =1.43一、离散型随机变量取值的平均值数学期望二、数学期望的性质 课堂小结三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则 作 业 P68/习题2.3/A组/2,3
