2.3.1 离散型随机变量的数学期望 课件(20张PPT)
文档属性
| 名称 | 2.3.1 离散型随机变量的数学期望 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 408.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:20:59 | ||
图片预览








文档简介
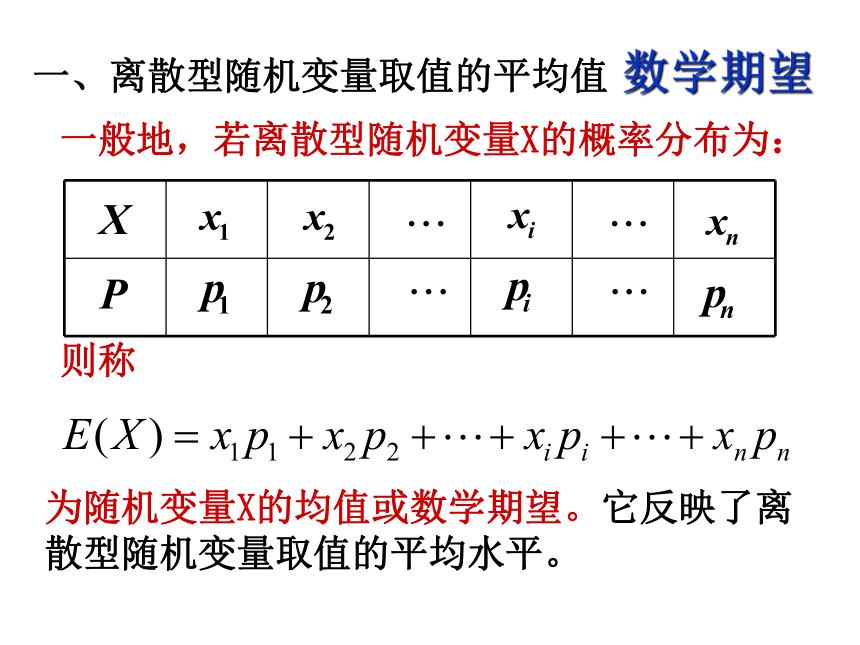
课件20张PPT。2.3.1离散型随机变量的均值高二数学 选修2-3 某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?把环数看成随机变量的概率分布列:一、互动探究一、离散型随机变量取值的平均值数学期望一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。 设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?思考:······························一、离散型随机变量取值的平均值数学期望二、数学期望的性质二、基础训练1、随机变量ξ的分布列是(1)则E(ξ)= . 2、随机变量ξ的分布列是2.4(2)若η=2ξ+1,则E(η)= . 5.8E(ξ)=7.5,则a= b= .0.40.1例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则三、例题讲解小结:例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2) 一般地,如果随机变量X服从二项布,即X~B(n,p),则小结:基础训练: 一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .3问1:是不是二项分布?问2:要不要考虑顺序?四、课堂小结一、离散型随机变量取值的平均值数学期望二、数学期望的性质三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则
(1) Y的分布列是什么?
(2) E(Y)=?思考:······························一、离散型随机变量取值的平均值数学期望二、数学期望的性质二、基础训练1、随机变量ξ的分布列是(1)则E(ξ)= . 2、随机变量ξ的分布列是2.4(2)若η=2ξ+1,则E(η)= . 5.8E(ξ)=7.5,则a= b= .0.40.1例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则三、例题讲解小结:例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2) 一般地,如果随机变量X服从二项布,即X~B(n,p),则小结:基础训练: 一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .3问1:是不是二项分布?问2:要不要考虑顺序?四、课堂小结一、离散型随机变量取值的平均值数学期望二、数学期望的性质三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则
