2.3.1离散型随机变量的均值(第一课时) 课件(24张PPT)
文档属性
| 名称 | 2.3.1离散型随机变量的均值(第一课时) 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:17:28 | ||
图片预览








文档简介
课件24张PPT。2.3.1 离散型随机变量的均值1.随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量随机变量常用字母X、Y、ξ、η等表示;2. 离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量3.离散型随机变量的分布列4. 分布列的两个性质:
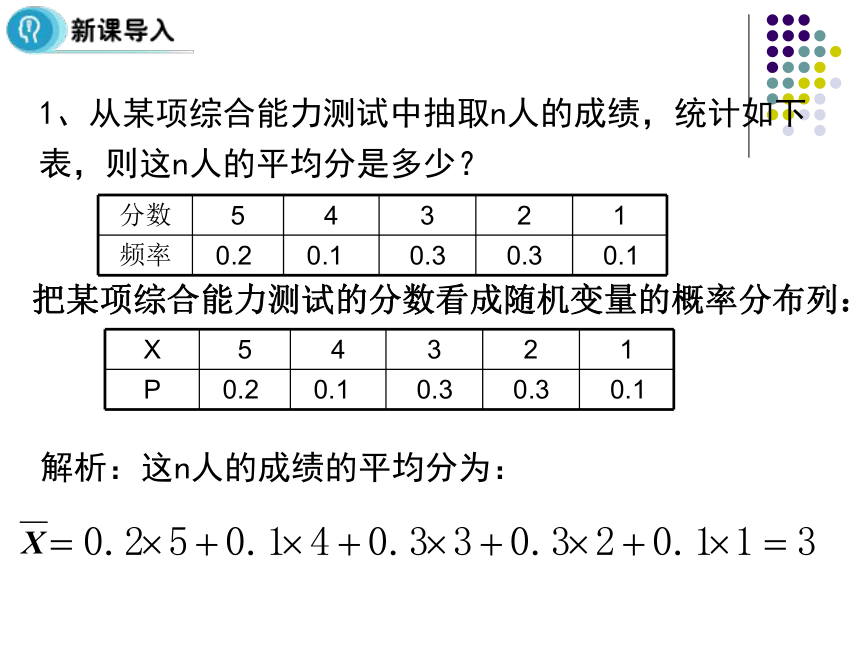
⑴P i ≥0,(i=1,2,…); ⑵ P1+P2+…+Pn=11、从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人的平均分是多少?解析:这100人的成绩的平均分为:1、从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人的平均分是多少?解析:这100人的成绩的平均分为:权数加权平均数1、从某项综合能力测试中抽取n人的成绩,统计如下表,则这n人的平均分是多少?解析:这n人的成绩的平均分为:把某项综合能力测试的分数看成随机变量的概率分布列:一、离散型随机变量取值的平均值一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?思考:······························数学期望的性质1、随机变量ξ的分布列是(1)则E(ξ)= . 2.4(2)若η=2ξ+1,则E(η)= . 5.82、随机变量ξ的分布列是E(ξ)=7.5,则a= b= .0.40.1归纳: 求离散型随机变量期望的步骤(1)确定离散型随机变量ξ的取值 (2)写出分布列,并检查分布列的正确与否 (3)求出期望 例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?解:罚球命中得分ξ的概率分布为例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则小结:E(X)=1?p+0?(1-p)=p超几何分布二项分布 一般地,如果随机变量X服从二项分布,即X~B(n,p),则小结:变式.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2)一、离散型随机变量取值的平均值数学期望二、数学期望的性质三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则谢谢 欣赏
⑴P i ≥0,(i=1,2,…); ⑵ P1+P2+…+Pn=11、从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人的平均分是多少?解析:这100人的成绩的平均分为:1、从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人的平均分是多少?解析:这100人的成绩的平均分为:权数加权平均数1、从某项综合能力测试中抽取n人的成绩,统计如下表,则这n人的平均分是多少?解析:这n人的成绩的平均分为:把某项综合能力测试的分数看成随机变量的概率分布列:一、离散型随机变量取值的平均值一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均水平。设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?思考:······························数学期望的性质1、随机变量ξ的分布列是(1)则E(ξ)= . 2.4(2)若η=2ξ+1,则E(η)= . 5.82、随机变量ξ的分布列是E(ξ)=7.5,则a= b= .0.40.1归纳: 求离散型随机变量期望的步骤(1)确定离散型随机变量ξ的取值 (2)写出分布列,并检查分布列的正确与否 (3)求出期望 例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?解:罚球命中得分ξ的概率分布为例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则小结:E(X)=1?p+0?(1-p)=p超几何分布二项分布 一般地,如果随机变量X服从二项分布,即X~B(n,p),则小结:变式.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2)一、离散型随机变量取值的平均值数学期望二、数学期望的性质三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则谢谢 欣赏
