2.3.2 离散型随机变量的方差 课件(18张PPT)
文档属性
| 名称 | 2.3.2 离散型随机变量的方差 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 417.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:15:46 | ||
图片预览






文档简介
课件18张PPT。2.3.2离散型随机变量的方差人教版选修2-3复习回顾1、离散型随机变量的数学期望2、数学期望的性质数学期望是反映离散型随机变量的平均水平若X服从两点分布则E(X)=p若X~B(n,p)则E(X)=np3、两个分布的数学期望探究点一 离散型随机变量的方差的概念问题一:统计甲、乙两名射手以往的成绩,得其击中目标靶的环数X1,X2的分布列分别如下:如果仅从平均射击成绩比较,能否区分甲、乙两人的射击水平? E(X1)=E(X2) =8,不能区分. 这意味着两名同学的平均射击水平没有差异那么还有其他刻画两名同学各自射击特点的指标吗?
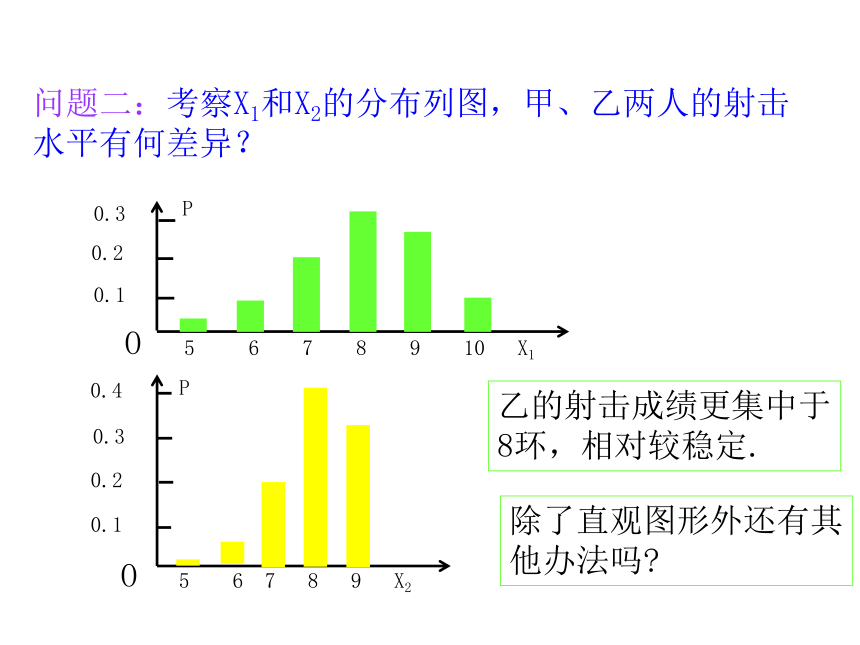
如果选一人参加比赛选谁参加竞赛呢?问题二:考察X1和X2的分布列图,甲、乙两人的射击水平有何差异?乙的射击成绩更集中于8环,相对较稳定.除了直观图形外还有其他办法吗?问题三:从分布列图观察随机变量相对于均值的偏离
程度,只是一种直观的定性分析,有时难以区分,理
论上需要有一个定量指标来反映.类似样本方差,能
否用 来刻画随机变量的稳定性?不妥!
还要考虑随机变量各个取值的权数.讲授新课若离散型随机变量X的分布列为D (X) =(x1-E(X))2·P1+ (x2-E(X))2·P2 + … + (xn- E(X))2·Pn
则 (xi-E(X))2 描叙了xi (i=1,2, …n)
相对于均值E(X)的偏离程度D(X)为这些偏离程度的加权平均,刻画了随机变量X
与其均值E(X)的平均偏离程度称D(X)为随机变量X的方差(1).方差的单位是随机变量的单位的平方;
标准差与随机变量的单位相同;注意:(2).随机变量的方差和标准差都反映了随机变量取值
偏离于均值的平均程度.(3).方差或标准差越小,则随机变量 偏离于均值的
平均程度越小.
思考:随机变量的方差与样本的方差有何联系与区别?随机变量的方差是常数,样本方差是随机变量已知X的分布列为
则D(X)等于 ( )
A.0.7 B.0.61 C.-0.3 D.0
【解析】选B.E(X)=-1×0.5+0×0.3+1×0.2=-0.3,
D(X)=0.5×(-1+0.3)2+0.3×(0+0.3)2+0.2×(1+0.3)2
=0.61.【即时训练】问题一:若随机变量X服从两点分布
X ~B( 1 , p ),则D(X)等于什么? D(X)=p(1-p). 问题二:若随机变量X服从二项分布
X ~B( 2 , p ),则D(X)等于什么? D(X)=2p(1-p). 探究点二 特殊分布列的方差及离散型随机变量的 方差的性质问题三:据归纳推理,若随机变量X服从二项分布 X ~B( n , p ),则D(X)等于什么?D(X)=np(1-p).问题四:若Y=aX+b,其中a,b为常数,则D(Y) 与D(X)有什么关系?由此可得什么结论?D(aX+b)=a2D(X).D(Y)=a2D(X),例1.随机抛掷一枚质地均匀的子,求向上一面的
点数X的均值,方差,和标准差解:抛掷子所得点数X的分布列为则学以致用 已知X的分布列为求:(1)E(X),D(X);
(2)设Y=2X+3,求E(Y),D(Y).
【变式练习】例2:有甲乙两个单位都愿意聘用你,而你能获得如下信息:根据工资待遇的差异情况,你愿意选择哪家单位?巩固练习:3、有一批数量很大的商品,其中次品占1%,现从中任意地连续取出200件商品,设其次品数为X,求E(X)和D(X)。117100.82,1.984.(全国)某商场经销某商品,根据以往资料统计,顾客采用的分起付款期数 的分布列为: 商场经销一件该商品,采用1期付款,其利润为200元,分2期或3期付款,其利润为250元,分4期或5期付款,其利润为300元, 表示经销一件该商品的利润。
(1)求事件A:”购买该商品的3位顾客中,至少有一位采用1期付款” 的概率P(A);
(2)求 的分布列及期望E( ) 。 离散型随机变量方差的性质离散型随机变量的方差 离散型随机变量方差的定义归纳求离散型随机变量方差的步骤①确定所有可能取值;②写出分布列;③求出均值④由方差的定义求出D(X).课 堂 小 结作业布置:再见思考:根据统计,一年中一个家庭万元以上的财产被盗的概率为0.01,保险公司开办一年期万元以上家庭财产保险,参加者需交保险费100元,若在一年以内,万元以上财产被盗,保险公司赔偿a元(a>100),问a如何确定,可使保险公司期望获利?教材P68 习题2.3
A组:1、 4 B组: 1, 2
如果选一人参加比赛选谁参加竞赛呢?问题二:考察X1和X2的分布列图,甲、乙两人的射击水平有何差异?乙的射击成绩更集中于8环,相对较稳定.除了直观图形外还有其他办法吗?问题三:从分布列图观察随机变量相对于均值的偏离
程度,只是一种直观的定性分析,有时难以区分,理
论上需要有一个定量指标来反映.类似样本方差,能
否用 来刻画随机变量的稳定性?不妥!
还要考虑随机变量各个取值的权数.讲授新课若离散型随机变量X的分布列为D (X) =(x1-E(X))2·P1+ (x2-E(X))2·P2 + … + (xn- E(X))2·Pn
则 (xi-E(X))2 描叙了xi (i=1,2, …n)
相对于均值E(X)的偏离程度D(X)为这些偏离程度的加权平均,刻画了随机变量X
与其均值E(X)的平均偏离程度称D(X)为随机变量X的方差(1).方差的单位是随机变量的单位的平方;
标准差与随机变量的单位相同;注意:(2).随机变量的方差和标准差都反映了随机变量取值
偏离于均值的平均程度.(3).方差或标准差越小,则随机变量 偏离于均值的
平均程度越小.
思考:随机变量的方差与样本的方差有何联系与区别?随机变量的方差是常数,样本方差是随机变量已知X的分布列为
则D(X)等于 ( )
A.0.7 B.0.61 C.-0.3 D.0
【解析】选B.E(X)=-1×0.5+0×0.3+1×0.2=-0.3,
D(X)=0.5×(-1+0.3)2+0.3×(0+0.3)2+0.2×(1+0.3)2
=0.61.【即时训练】问题一:若随机变量X服从两点分布
X ~B( 1 , p ),则D(X)等于什么? D(X)=p(1-p). 问题二:若随机变量X服从二项分布
X ~B( 2 , p ),则D(X)等于什么? D(X)=2p(1-p). 探究点二 特殊分布列的方差及离散型随机变量的 方差的性质问题三:据归纳推理,若随机变量X服从二项分布 X ~B( n , p ),则D(X)等于什么?D(X)=np(1-p).问题四:若Y=aX+b,其中a,b为常数,则D(Y) 与D(X)有什么关系?由此可得什么结论?D(aX+b)=a2D(X).D(Y)=a2D(X),例1.随机抛掷一枚质地均匀的子,求向上一面的
点数X的均值,方差,和标准差解:抛掷子所得点数X的分布列为则学以致用 已知X的分布列为求:(1)E(X),D(X);
(2)设Y=2X+3,求E(Y),D(Y).
【变式练习】例2:有甲乙两个单位都愿意聘用你,而你能获得如下信息:根据工资待遇的差异情况,你愿意选择哪家单位?巩固练习:3、有一批数量很大的商品,其中次品占1%,现从中任意地连续取出200件商品,设其次品数为X,求E(X)和D(X)。117100.82,1.984.(全国)某商场经销某商品,根据以往资料统计,顾客采用的分起付款期数 的分布列为: 商场经销一件该商品,采用1期付款,其利润为200元,分2期或3期付款,其利润为250元,分4期或5期付款,其利润为300元, 表示经销一件该商品的利润。
(1)求事件A:”购买该商品的3位顾客中,至少有一位采用1期付款” 的概率P(A);
(2)求 的分布列及期望E( ) 。 离散型随机变量方差的性质离散型随机变量的方差 离散型随机变量方差的定义归纳求离散型随机变量方差的步骤①确定所有可能取值;②写出分布列;③求出均值④由方差的定义求出D(X).课 堂 小 结作业布置:再见思考:根据统计,一年中一个家庭万元以上的财产被盗的概率为0.01,保险公司开办一年期万元以上家庭财产保险,参加者需交保险费100元,若在一年以内,万元以上财产被盗,保险公司赔偿a元(a>100),问a如何确定,可使保险公司期望获利?教材P68 习题2.3
A组:1、 4 B组: 1, 2
